Notació de Coxeter

En geometria, la notació de Coxeter (o símbol de Coxeter) és un sistema de classificació de grups de simetria, que descriu els angles entre les reflexions fonamentals d'un grup de Coxeter en una notació entre claudàtors que expressa l'estructura d'un diagrama de Coxeter-Dynkin, amb modificadors per indicar determinats subgrups. La notació rep el nom de H. S. M. Coxeter, i ha estat definida de forma més comprensible per Norman Johnson.

Dominis fonamentals de grups de punts 3D reflexius
, [ ]=[1] C_1v	, [2] C_2v	, [3] C_3v	, [4] C_4v	, [5] C_5v	, [6] C_6v
Ordre 2	Ordre 4	Ordre 6	Ordre 8	Ordre 10	Ordre 12
[2]=[2,1] D_1h	[2,2] D_2h	[2,3] D_3h	[2,4] D_4h	[2,5] D_5h	[2,6] D_6h
Ordre 4	Ordre 8	Ordre 12	Ordre 16	Ordre 20	Ordre 24
, [3,3], T_d		, [4,3], O_h		, [5,3], I_h
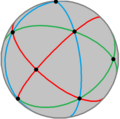Ordre 24		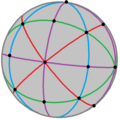Ordre 48		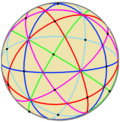Ordre 120
La notació de coxeter expressa els grups de Coxeter com una llista d'ordres de branques d'un diagrama de Coxeter, com els grups polièdrics, = [p,q]. Els grups dièdrics, , poden expressar-se un producte [ ]×[n] o en un sol símbol amb un explícit ordre 2 de branques, [2,n]

Grups reflexius[modifica]

Per als grups de Coxeter, definits per reflexions pures, hi ha una correspondència directa entre la notació entre claudàtors i el diagrama de Coxeter-Dynkin. Els nombres de l'anotació entre claudàtors representen els ordres de reflexió dels miralls a les branques del diagrama de Coxeter. Utilitza la mateixa simplificació, suprimint els «2» entre miralls ortogonals.

La notació de Coxeter se simplifica amb exponents per representar el nombre de branques d'una fila per a un diagrama lineal. Així, el grup A_n es representa amb [3^n-1], a l'implicar n nodes connectats amb n-1 branques d'ordre 3. Per exemple, A₂ = [3,3] = [3²] o [3^1,1] representa els diagrames o .

Inicialment, Coxeter representava esquemes bifurcadors amb posicionament vertical dels números, però després ho va abreujar amb una notació exponencial, com [...,3^p,q] o [3^p,q,r], començant per [3^1,1,1] o [3,3^1,1] = o com a D₄. Coxeter va tractar als zeros com a casos especials per adaptar-se a la família A_n, com A₃ = [3,3,3,3] = [3^4,0,0] = [3^4,0] = [3^3,1] = [3^2,2], per a = = .

Els grups de Coxeter formats per esquemes cíclics estan representats entre parèntesis dins dels claudàtors, com [(p,q,r)] = per al grup triangular (p q r). Si els ordres de la branca són iguals, es poden agrupar com a exponent a la longitud del cicle entre claudàtors, com [(3,3,3,3)] = [3^[4]], per a representar el diagrama de Coxeter o . , que també es pot representar [3,(3,3,3)] o [3,3^[3]].

També es poden expressar, amb molta cura, esquemes de bucles més complicats. El grup de Coxeter paracompacte pot ser representat per la notació de Coxeter [(3,3,(3),3,3)], amb parèntesis anidats / superposats, mostrant dos bucles [(3,3,3)] adjacents, i també es representa de manera més compacta com [3^{[ ]×[ ]}], que representa la simetria ròmbica en el diagrama de Coxeter. El diagrama gràfic complet del paracompacte o , es representa com [3^[3,3]] amb el superíndex [3,3] com la simetria del seu diagrama de coxeter del tetraedre regular.

El diagrama de Coxeter sol deixar les ramificacions d'ordre 2 no-tancades, però la notació entre claudàtors inclou un 2 explícit per connectar els subgrafs. Així, el diagrama de Coxeter = A₂×A₂ = 2A₂ també es por representar com [3]×[3] = [3]² = [3,2,3]. De vegades es poden incloure dues branques explícites amb una etiqueta 2 o bé amb una línia amb un buit: o , com a presentació idèntica com [3,2,3].

Grups finits
Rang	Símbol del grup	Notació entre claudàtors	Diagrama Coxeter
2	A₂	[3]
2	B₂	[4]
2	H₂	[5]
2	G₂	[6]
2	I₂(p)	[p]
3	I_h, H₃	[5,3]
3	T_d, A₃	[3,3]
3	O_h, B₃	[4,3]
4	A₄	[3,3,3]
4	B₄	[4,3,3]
4	D₄	[3^1,1,1]
4	F₄	[3,4,3]
4	H₄	[5,3,3]
n	A_n	[3^n-1]	..
n	B_n	[4,3^n-2]	...
n	D_n	[3^n-3,1,1]	...
6	E₆	[3^2,2,1]
7	E₇	[3^3,2,1]
8	E₈	[3^4,2,1]

Grups afins
Símbol del grup	Notació entre claudàtors	Diagrama Coxeter
${\tilde {I}}_{1},{\tilde {A}}_{1}$	[∞]
${\tilde {A}}_{2}$	[3^[3]]
${\tilde {C}}_{2}$	[4,4]
${\tilde {G}}_{2}$	[6,3]
${\tilde {A}}_{3}$	[3^[4]]
${\tilde {B}}_{3}$	[4,3^1,1]
${\tilde {C}}_{3}$	[4,3,4]
${\tilde {A}}_{4}$	[3^[5]]
${\tilde {B}}_{4}$	[4,3,3^1,1]
${\tilde {C}}_{4}$	[4,3,3,4]
${\tilde {D}}_{4}$	[ 3^1,1,1,1]
${\tilde {F}}_{4}$	[3,4,3,3]
${\tilde {A}}_{n}$	[3^[n+1]]	... o ...
${\tilde {B}}_{n}$	[4,3^n-3,3^1,1]	...
${\tilde {C}}_{n}$	[4,3^n-2,4]	...
${\tilde {D}}_{n}$	[ 3^1,1,3^n-4,3^1,1]	...
${\tilde {E}}_{6}$	[3^2,2,2]
${\tilde {E}}_{7}$	[3^3,3,1]
${\tilde {E}}_{8}=E_{9}$	[3^5,2,1]

Grups hiperbòlics
Símbol del grup	Notació entre claudàtors	Diagrama Coxeter
	[p,q] amb 2(p+q)<pq
	[(p,q,r)] amb ${\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}<1$
${\overline {BH}}_{3}$	[4,3,5]
${\overline {K}}_{3}$	[5,3,5]
${\overline {J}}_{3},{\tilde {H}}_{3}$	[3,5,3]
${\overline {DH}}_{3}$	[5,3^1,1]
${\widehat {AB}}_{3}$	[(3,3,3,4)]
${\widehat {AH}}_{3}$	[(3,3,3,5)]
${\widehat {BB}}_{3}$	[(3,4,3,4)]
${\widehat {BH}}_{3}$	[(3,4,3,5)]
${\widehat {HH}}_{3}$	[(3,5,3,5)]
${\overline {H}}_{4},{\tilde {H}}_{4},H_{5}$	[3,3,3,5]
${\overline {BH}}_{4}$	[4,3,3,5]
${\overline {K}}_{4}$	[5,3,3,5]
${\overline {DH}}_{4}$	[5,3,3^1,1]
${\widehat {AF}}_{4}$	[(3,3,3,3,4)]

Per als grups afins i hiperbòlics, el subíndex és inferior al nombre de nodes en cada cas, ja que cadascun d'aquests grups es va obtenir afegint un node al diagrama d'un grup finit.

Subgrups[modifica]

La notació de Coxeter representa la simetria rotacional / translacional afegint un operador superíndex ⁺ fora dels claudàtors, [X]⁺ que redueix l'ordre del grup [X] a la meitat, per tant un subgrup d'índex 2. Aquest operador implica que s'hagi d'aplicar un nombre parell d'operadors, substituint les reflexions per rotacions (o traduccions). Quan s'aplica a un grup de Coxeter es denomina «subgrup directe» perquè el que queda només són isometries directes sense simetria reflexiva.

Els operadors ⁺ també es poden aplicar dins dels claudàtors, com [X,Y⁺] o [X,(Y,Z)⁺], i crea «subgrups semidirectes» que poden incloure generadors reflexius i no-reflexius. Els subgrups semidirectes només poden aplicar-se als subgrups del grup de Coxeter que tenen ordres parells de branques adjacents a ell. Els elements entre parèntesis dins d'un grup de Coxeter poden donar-se a un operador de superíndex ⁺, tenint com a efecte dividir les branques ordenades adjacents a mig ordre, per tant sol aplicar-se només amb números parells. Per exemple, [4,3⁺] i [4,(3,3)⁺] ().

Si s'aplica amb una branca senar contigua, no crea un subgrup d'índex 2, sinó que crea dominis fonamentals solapats, com [5,1⁺] = [5/2], que pot definir polígons doblement embolicats com un pentagrama, {5/2}, i [5,3⁺], que es relacionen amb el triangle de Schwarz [5/2,3], densitat 2.

Exemples en grups de rang 2
Grup	Ordre	Generadors	Subgrup		Ordre	Generadors	Notes
[p]	2p	{0,1}	[p]⁺		p	{01}	Subgrup directe
[2p⁺] = [2p]⁺	2p	{01}	[2p⁺]⁺ = [2p]⁺² = [p]⁺		p	{0101}	Subgrup directe
[2p]	4p	{0,1}	[1⁺,2p] = [p]	= =	2p	{101,1}	Subgrups semidirectes
			[2p,1⁺] = [p]	= =	2p	{0,010}	Subgrups semidirectes
			[1⁺,2p,1⁺] = [2p]⁺² = [p]⁺	= =	p	{0101}	Quart de subgrup

Es poden veure grups sense elements ⁺ veïns en nodes anellats en el diagrama de Coxeter-Dynkin per a politops uniformes i grups del paper pintat relacionats amb «nodes forats» al voltant dels elements ⁺, cercles buits amb els nodes alternats eliminats. Així doncs, el cub xato té simetria [4,3]⁺ (), el tetraedre xato té simetria [4,3⁺] (), i un demicub h{4,3} = {3,3} ( o = ) té simetria [1⁺,4,3] = [3,3] ( o = = ).

Nota: La simetria piritèdrica es pot escriure com , separant el graf amb buits per a la claredat, amb els generadors {0,1,2} del grup de Coxeter produint generadors piritèdrics {0,12}, un reflex i una rotació de 3-plecs. I la simetria tetraedral quiral es pot escriure com o , [1⁺,4,3⁺] = [3,3]⁺, amb generadors {12,0120}.

Subgrups reduïts a la meitat i grups ampliats[modifica]

Norman Johnson estén l'operador ⁺ per a que sigui un marcador de posició 1⁺ nodes, que elimina els miralls, doblant la mida del domini fonamental i retallant l'ordre del grup a la meitat.^[1] En general, aquesta operació només s'aplica a miralls individuals delimitats per branques d'ordre parell. L'1 representa un mirall, de manera que [2p] es pot veure com [2p,1], [1,2p], o [1,2p,1], com un diagrama o , amb 2 miralls relacionats per un angle diedre d'ordre 2p. L'efecte d'una eliminació del mirall és duplicar nodes de connexió, que es poden veure en els diagrames de Coxeter: = , o en la notació entre claudàtors: [1⁺,2p, 1] = [1,p,1] = [p].

Exemple d'operacions de reducció a la meitat

[1,4,1] = [4]	= = [1⁺,4,1]=[2]=[ ]×[ ]

= = [1,4,1⁺]=[2]=[ ]×[ ]	= = = [1⁺,4,1⁺] = [2]⁺

Cadascun d'aquests miralls es pot eliminar de manera que h[2p] = [1⁺,2p,1] = [1,2p,1⁺] = [p] és un subgrup reflectant d'índex 2. Això es pot mostrar en un diagrama de Coxeter mitjançant afegint un símbol ⁺ a sobre del node: = = .

Si s'eliminen els dos miralls, es genera un quart de subgrup, i l'ordre de la branca es converteix en un punt de gir de la meitat de l'ordre:

q[2p] = [1⁺,2p,1⁺] = [p]⁺, és un subgrup rotacional d'índex 4.

=

.

Per exemple, (amb p=2): [4,1⁺] = [1⁺,4] = [2] = [ ]×[ ], ordre 4. [1⁺,4,1⁺] = [2]⁺, ordre 2.

El contrari a la reducció a la mitat és la duplicació,^[2] la qual afegeix un mirall, es bisecta un domini fonamental i es duplica l'ordre grupal.

[[p]] = [2p]

Les operacions de reducció a la meitat s'apliquen per a grups de rang superior (com la simetria tetraedral, que és un mig grup del grup octaedral: h[4,3] = [1⁺,4,3] = [3,3], eliminant la meitat dels miralls fins a les 4 branques). L'efecte d'una eliminació del mirall és duplicar tots els nodes de connexió, que es poden veure als diagrames de Coxeter: = , h[2p,3] = [1⁺,2p,3] = [(p,3,3)].

Simetria tetraedral	Simetria octaedral
T_d, [3,3] = [1⁺,4,3] = = (Ordre 24)	O_h, [4,3] = [[3,3]] (Ordre 48)

Si s'indexen nodes, es poden etiquetar mig subgrups amb nous miralls com a compostos. Igual que , generadors {0,1} té el subgrup = , generadors {1,010}, on s'elimina el mirall 0 i es substitueix per una còpia del mirall 1 reflectit al mirall. També es dòna en , generadors {0,1,2}, té el mig grup = , generadors {1,2,010}.

Doblant afegint un mirall també s'aplica en invertir l'operació a la meitat: [[3,3]] = [4,3], o de manera més general [[(q,q,p)]] = [2p,q].

Subgrups radicals[modifica]

Norman Johnson també va afegir un operador asterisc o estrella * per a «subgrups radicals»,^[3] que actua de manera similar a l'operador ⁺, però elimina la simetria rotacional. L'índex del subgrup radical és l'ordre de l'element eliminat. Per exemple, [4,3*] ≅ [2,2]. El subgrup [3] eliminat és d'ordre 6 de manera que [2,2] és un subgrup d'índex 6 de [4,3].

Un subgrup radical és similar a una alternança, però elimina els generadors de rotació

Els subgrups radicals representen l'operació inversa a una operació de simetria estesa. Per exemple, [4,3*] ≅ [2,2], i a l'inversa [2,2] es poden ampliar com a [3[2,2]] ≅ [4,3]. Els subgrups també es poden expressar com a diagrama de Coxeter: o ≅ . El node eliminat (mirall) fa que els miralls virtuals del mirall adjacent es converteixin en miralls reals.

Si [4,3] té generadors {0,1,2}, [4,3⁺], índex 2, té generadors {0,12}; [1⁺,4,3] ≅ [3,3], l'índex 2 té generadors {010,1,2}; mentre que el subgrup radical [4,3*] ≅ [2,2], índex 6, té generadors {01210, 2, (012)³}; i finalment [1⁺,4,3*], l'índex 12 té generadors {0(12)²0, (012)²01}.

Subgrups triònics[modifica]

Un subgrup trionic són subgrups d'índex 3. Hi ha molts que Johnson defineix com subgrup trionic amb l'operador ⅄, índex 3. Per als grups coxeter de rang 2, [3], el subgrup trionic, [3^⅄] és [ ], un únic mirall. I per a [3p], el subgrup trionic és [3p]^⅄ ≅ [p]. Donat el node , amb generadors {0,1}, té 3 subgrups trionics. Es poden diferenciar posant el símbol ⅄ després del generador de miralls per eliminar-lo, o bé en una branca per a tots dos: [3p,1^⅄] = = , = , i [3p^⅄] = = amb generadors {0,10101}, {01010,1}, o {101,010}.

Els subgrups trionics de simetria tetraèdrica: [3,3]^⅄ ≅ [2⁺,4], relacionen la simetria del tetràedre regular i el disfenoide tetragonal.

Per als grups de Coxeter de rang 3, [p,3], hi ha un subgrup trionic [p,3^⅄] ≅ [p/2,p], o = . Per exemple, el grup finit [4,3^⅄] ≅ [2,4], i el grup Euclidià [6,3^⅄] ≅ [3,6], i el grup hiperbòlic [8,3^⅄] ≅ [4,8].

Exemple de subgrups triònics rang 2, [6] amb línies de miralls de 3 colors
Grups triònics de rang 3
Grups triònics de rang 4

Per a una branca adjacent senar, p, no és reduirà l'ordre de grup, sinó que es crearan dominis fonamentals superposats. L'ordre de grup es manté igual, mentre que la densitat augmenta. Per exemple, la simetria icosaèdrica, [5,3], del poliedre regular icosaedre es converteix en [5/2,5], la simetria de dos políedres d'estrelles regulars. També relaciona els mosaics hiperbòlics {p,3} i mosaics hiperbòlics estrella {p/2,p}.

Per a rang 4, [q,2p,3^⅄] = [2p,((p,q,q))], = .

Per exemple, [3,4,3^⅄] = [4,3,3], o = , generadors {0,1,2,3} en [3,4,3] amb el subgrup triònic [4,3,3] generadors {0,1,2,32123}. Per a grups hiperbòlics, [3,6,3^⅄] = [6,3^[3]], i [4,4,3^⅄] = [4,4,4].

Exemple de subgrup triònic en simetria octaedral: [4,3^⅄] = [2,4]
Exemple de subgrup triònic en simetria hexagonal [6,3] mapejat cap a una simetria [6,3] més gran
Exemple de subgrup triònic en simetria octagonal [8,3] mapejat cap a una simetria [4,8] més gran

Subgrups triònics de simetria tetraedral[modifica]

Johnson va identificar dos subgrups trionics de [3,3]:^[4]

Primer, un subgrup d'índex 3, [3,3]^⅄ ≅ [2⁺,4], amb [3,3] ( = = ) generadors {0,1,2}. També es pot escriure com [(3,3,2^⅄)] () com a recordatori dels seus generadors {02,1}. Aquesta reducció de simetria és la relació entre el tetraedre i el disfenoide tetragonal, representant un estirament d'un tetràedre perpendicular a dues arestes oposades.
En segon lloc, identifica un subgrup d'índex 6 relacionat [3,3]^Δ o [(3,3,2^⅄)]⁺ (), índex 3 de [3,3]⁺ ≅ [2,2]⁺, amb generadors {02,1021}, de [3,3] i els seus generadors {0,1,2}. Aquests subgrups també s'apliquen dins de grups més grans de Coxeter amb subgrup [3,3] amb totes les branques veïnes ordenades en parelles.

Aquests subgrups també s'apliquen dins de grups més grans de Coxeter amb subgrup [3,3] amb totes les branques veïnes ordenades en parelles.

[3,3]^⅄ ≅ [2⁺,4] com un dels tres conjunts de 2 miralls ortogonals en projecció estereogràfica. El vermell, el verd i el blau representen 3 jocs de miralls, i les línies grises s'extreuen els miralls, realitzant dues rotacions (diamants morats)
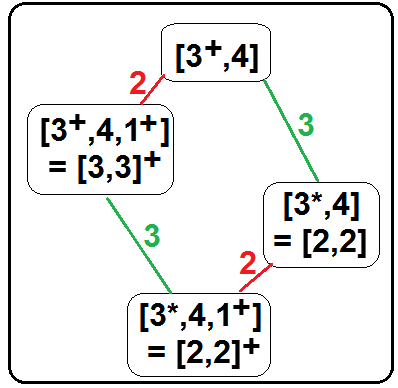
Relacions triòniques de [3,3]
Relacions de subgrups triònics de [3,3,4]

Per exemple, [(3,3)⁺,4], [(3,3)^⅄,4], i [(3,3)^Δ,4] són subgrups [3,3,4], índex 2, 3 i 6 respectivament. Els generadors de [(3,3)^⅄,4] ≅ [[4,2,4]] ≅ [8,2⁺,8], ordre 128, són {02,1,3} de [3,3,4] generadors {0,1,2,3}. I [(3,3)^Δ,4] ≅ [[4,2⁺,4]], ordre 64, són generadors {02,1021,3}. També [3^⅄,4,3^⅄] ≅ [(3,3)^⅄,4].

Els també relacionats [3^1,1,1] = [3,3,4,1⁺] són subgrups triònics: [3^1,1,1]^⅄ = [(3,3)^⅄,4,1⁺], ordre 64, i 1=[3^1,1,1]^Δ = [(3,3)^Δ,4,1⁺] ≅ [[4,2⁺,4]]⁺, ordre 32.

Inversió central[modifica]

Una inversió central, d'ordre 2, és operativament diferent per dimensió. El grup ⁿ = [2^n-1] representa n miralls ortogonals en un espai n-dimensional, o un n-pla d'un subespai d'un espai dimensional superior. Els miralls del grup [2^n-1] són numerats $0 ... n-1$ . L'ordre dels miralls no importa en cas d'inversió. La matriu d'una inversió central és $-I$ , la matriu identitat amb -1 a la diagonal.

A partir d'aquesta base, la inversió central té un generador com a producte de tots els miralls ortogonals. En la notació de Coxeter aquest grup d'inversió s'expressa afegint una alternança ⁺ a cada 2 branques. La simetria d'alternança està marcada als nodes del diagrama de Coxeter com a nodes oberts.

Un diagrama de Coxeter-Dynkin es pot marcar amb dues branques explícites que defineixen una seqüència lineal de miralls, nodes oberts i nodes doble obert compartits per mostrar l'encadenament dels generadors de reflexió.

Per exemple, [2⁺,2] i [2,2⁺] són subgrups d'índex 2 de [2,2], , i són representats com (o ) i (o ) amb generadors {01,2} i {0,12} respectivament. El seu subgrup comú d'índex 4 és [2⁺,2⁺], i és representat com (o ), amb el doble obert marcant un node compartit en les dues alternances i un únic generador per rotoreflexió {012}.

Dimensió	Notació de Coxeter	Ordre	Operació	Generador
2	[2]⁺	2	180° rotació, C₂	{01}
3	[2⁺,2⁺]	2	rotoreflexió, C_i o S₂	{012}
4	[2⁺,2⁺,2⁺]	2	doble rotació	{0123}
5	[2⁺,2⁺,2⁺,2⁺]	2	doble reflexió rotativa	{01234}
6	[2⁺,2⁺,2⁺,2⁺,2⁺]	2	triple rotació	{012345}
7	[2⁺,2⁺,2⁺,2⁺,2⁺,2⁺]	2	triple reflexió rotativa	{0123456}

Rotacions i reflexos rotatius[modifica]

Les rotacions i els reflexos rotatius estan construïts per un producte d'un sol generador de tots els reflexos d'un grup prismàtic, [2p]×[2q]× ... on mcd (p,q)=1, són isomorfs al grup cíclic abstracte Z_n, d'ordre n=2pq.

Les rotacions dobles en 4 dimensions, [2p⁺,2⁺,2q⁺] (amb mcd (p,q)=1), que inclouen un grup central, i són expressades per Conway com ±[C_p×C_q],^[5] ordre 2pq. A partir del diagrama de Coxeter , els generadors {0,1,2,3}, el generador únic de [2p⁺,2⁺,2q⁺], és {0123}. El semigrup [2p⁺,2⁺,2q⁺]⁺, o graf cíclic,[(2p⁺,2⁺,2q⁺,2⁺)], , és expressat per Conway com [C_p×C_q], ordre pq, amb generador {01230123}.

Si hi ha un factor comú f, la doble rotació es pot escriure com ¹⁄_f [2pf⁺,2⁺,2qf⁺] (amb mcd (p,q)=1), generador {0123}, ordre 2pqf. Per exemple, p=q=1, f=2, ¹⁄₂[4⁺,2⁺,4⁺] és d'ordre 4. I ¹⁄_f [2pf⁺,2⁺,2qf⁺]⁺, generador {01230123}, és d'ordre pqf. Per exemple, ¹⁄₂[4⁺,2⁺,4⁺]⁺ és d'ordre 2, una inversió central.

Exemples
Dimensió	Notació de Coxeter	Ordre	Operació	Generador	Subgrup directe
2	[2p]⁺	2p	Rotació	{01}	[2p]⁺²	Rotació simple: [2p]⁺² = [p]⁺ ordre p
3	[2p⁺,2⁺]		rotoreflexió	{012}	[2p⁺,2⁺]⁺
4	[2p⁺,2⁺,2⁺]		doble rotació	{0123}	[2p⁺,2⁺,2⁺]⁺
5	[2p⁺,2⁺,2⁺,2⁺]		doble reflexió rotativa	{01234}	[2p⁺,2⁺,2⁺,2⁺]⁺
6	[2p⁺,2⁺,2⁺,2⁺,2⁺]		triple rotació	{012345}	[2p⁺,2⁺,2⁺,2⁺,2⁺]⁺
7	[2p⁺,2⁺,2⁺,2⁺,2⁺,2⁺]		triple reflexió rotativa	{0123456}	[2p⁺,2⁺,2⁺,2⁺,2⁺,2⁺]⁺
4	[2p⁺,2⁺,2q⁺]	2pq	doble rotació	{0123}	[2p⁺,2⁺,2q⁺]⁺	Doble rotació: [2p⁺,2⁺,2q⁺]⁺ ordre pq mcd(p,q)=1
5	[2p⁺,2⁺,2q⁺,2⁺]		doble reflexió rotativa	{01234}	[2p⁺,2⁺,2q⁺,2⁺]⁺
6	[2p⁺,2⁺,2q⁺,2⁺,2⁺]		triple rotació	{012345}	[2p⁺,2⁺,2q⁺,2⁺,2⁺]
7	[2p⁺,2⁺,2q⁺,2⁺,2⁺,2⁺]		triple reflexió rotativa	{0123456}	[2p⁺,2⁺,2q⁺,2⁺,2⁺,2⁺]⁺
6	[2p⁺,2⁺,2q⁺,2⁺,2r⁺]	2pqr	triple rotació	{012345}	[2p⁺,2⁺,2q⁺,2⁺,2r⁺]⁺	Triple rotació: [2p⁺,2⁺,2q⁺,2⁺,2r⁺]⁺ ordre pqr mcd(p,q,r)=1
7	[2p⁺,2⁺,2q⁺,2⁺,2r⁺,2⁺]	2pqr	triple reflexió rotativa	{0123456}	[2p⁺,2⁺,2q⁺,2⁺,2r⁺,2⁺]⁺

Subgrups comutadors[modifica]

Els grups simples amb només elements de branques d'ordre imparell tenen només un subgrup de rotació / translació d'ordre 2, que també és el subgrup commutador, per exemple 3,3⁺, [3,5]⁺, [3,3,3]⁺, [3,3,5]⁺. Per a altres grups de Coxeter amb branques d'ordre parell, el subgrup commutator té l'índex 2^c, on c és el nombre de subgrafes desconnectats quan s'eliminen totes les branques d'ordre parell.^[6] Per exemple, [4,4] té tres nodes independents al diagrama de Coxeter quan s'eliminen els «4», de manera que el seu subgrup de commutador és l'índex 2³, i pot tenir diferents representacions, totes amb tres operadors ⁺: [4⁺,4⁺]⁺, [1⁺,4,1⁺,4,1⁺], [1⁺,4,4,1⁺]⁺, o [(4⁺,4⁺,2⁺)]. Es pot fer servir una notació general amb +c com a exponent de grup, com [4,4]⁺³.

Exemples de subgrups[modifica]

Exemples de subgrups de rang 2[modifica]

Els grups de simetria diedral amb ordres parells tenen diversos subgrups. Aquest exemple mostra dos miralls generadors de [4] en vermell i verd, i mira a tots els subgrups per la meitat, la reducció de rang i els seus subgrups directes. El grup [4], té dos generadors de miralls 0 i 1. Cadascun genera dos miralls virtuals 101 i 010 per reflexió entre els altres.

Subgrups de [4]
Índex	1	2 (meitat)		4 (reducció de rang)
Diagrama
Coxeter	[1,4,1] = [4]	= = [1⁺,4,1] = [1⁺,4] = [2]	= = [1,4,1⁺] = [4,1⁺] = [2]	[1] = [ ]	[1] = [ ]
Generadors	{0,1}	{101,1}	{0,010}	{0}	{1}
Subgrups directes
Índex	2	4		8
Diagrama
Coxeter	[4]⁺	= = = [4]⁺² = [1⁺,4,1⁺] = [2]⁺		[ ]⁺
Generadors	{01}	{(01)²}		{0²} = {1²} = {(01)⁴} = { }

Exemples de subgrups de rang 3 euclidians[modifica]

El grup [4,4] compta amb 15 petits índex de subgrups. Aquesta taula els mostra tots, amb un domini fonamental groc per a grups reflectants purs i alternant dominis blancs i blaus que es combinen per fer dominis rotatius. Les línies de mirall cian, vermell i verd corresponen als nodes de colors del diagrama de Coxeter. Els generadors de subgrups es poden expressar com a productes dels tres miralls originals del domini fonamental, {0,1,2}, que corresponen als 3 nodes del diagrama de Coxeter, . Un producte de dues línies de reflexió que s'entrecreuen fa una rotació, com {012}, {12} o {02}. Eliminar un mirall provoca dues còpies de miralls veïns, a través del mirall eliminat, com {010} i {212}. Dues rotacions en sèrie tallen l'ordre de rotació a la meitat, com {0101} o {(01)²}, {1212} o {(02)²}. Un producte dels tres miralls crea una transreflexió, com {012} o {120}.

Subgrups d'índex petit de [4,4]
Índex	1	2			4
Diagrama
Coxeter	[1,4,1,4,1] = [4,4]	[1⁺,4,4] =	[4,4,1⁺] =	[4,1⁺,4] =	[1⁺,4,4,1⁺] =	[4⁺,4⁺]
Generadors	{0,1,2}	{010,1,2}	{0,1,212}	{0,101,121,2}	{010,1,212,20102}	{(01)²,(12)²,012,120}
Orbifold	*442			*2222		22×
Subgrups semidirectes
Índex		2			4
Diagrama
Coxeter		[4,4⁺]	[4⁺,4]	[(4,4,2⁺)] =	[4,1⁺,4,1⁺] = =	[1⁺,4,1⁺,4] = =
Generadors		{0,12}	{01,2}	{02,1,212}	{0,101,(12)²}	{(01)²,121,2}
Orbifold		4*2		2*22
Subgrups directes
Index	2	4			8
Diagrama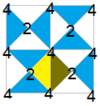
Coxeter	[4,4]⁺ =	[4,4⁺]⁺ =	[4⁺,4]⁺ =	[(4,4,2⁺)]⁺ =	[4,4]⁺³ = [(4⁺,4⁺,2⁺)] = [1⁺,4,1⁺,4,1⁺] = [4⁺,4⁺]⁺ = = = =
Generadors	{01,12}	{(01)²,12}	{01,(12)²}	{02,(01)²,(12)²}	{(01)²,(12)²,2(01)²2}
Orbifold	442			2222
Subgrups radicals
Índex		8		16
Diagrama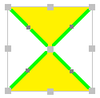
Coxeter		[4,4*] =	[4*,4] =	[4,4*]⁺ =	[4*,4]⁺ =
Orbifold		*2222		2222

Exemples de grups hiperbòlics[modifica]

El mateix conjunt de 15 petits subgrups existeix en tots els grups de triangles amb elements d'ordre parell, com [6,4] en el pla hiperbòlic:

Subgrups d'índex petit de [6,4]
Índex	1	2			4
Diagrama
Coxeter	[1,6,1,4,1] = [6,4]	[1⁺,6,4] =	[6,4,1⁺] =	[6,1⁺,4] =	[1⁺,6,4,1⁺] =	[6⁺,4⁺]
Generadors	{0,1,2}	{010,1,2}	{0,1,212}	{0,101,121,2}	{010,1,212,20102}	{(01)²,(12)²,012}
Orbifold	*642	*443	*662	*3222	*3232	32×
Subgrups semidirectes
Diagrama
Coxeter		[6,4⁺]	[6⁺,4]	[(6,4,2⁺)]	[6,1⁺,4,1⁺] = = = =	[1⁺,6,1⁺,4] = = = =
Generadors		{0,12}	{01,2}	{02,1,212}	{0,101,(12)²}	{(01)²,121,2}
Orbifold		4*3	6*2	2*32	2*33	3*22
Subgrups directes
Índex	2	4			8
Diagrama
Coxeter	[6,4]⁺ =	[6,4⁺]⁺ =	[6⁺,4]⁺ =	[(6,4,2⁺)]⁺ =	[6⁺,4⁺]⁺ = [1⁺,6,1⁺,4,1⁺] = = =
Generators	{01,12}	{(01)²,12}	{01,(12)²}	{02,(01)²,(12)²}	{(01)²,(12)²,201012}
Orbifold	642	443	662	3222	3232
Subgrups radicals
Índex		8	12	16	24
Diagrama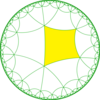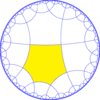
Coxeter (Orbifold)		[6,4] = (3333)	[6,4] (222222)	[6,4]⁺ = EN TR JP RU DE €4.95 / month Favourites List Audio Listining Color Mode Monthly New Updates Fullname Email * Credit or debit card A PHP Error was encountered Severity: Notice Message: Undefined variable: userid Filename: user/popup_modal.php Line Number: 68 Backtrace: File: /home/ah0ejbmyowku/public_html/application/views/user/popup_modal.php Line: 68 Function: _error_handler File: /home/ah0ejbmyowku/public_html/application/views/page/index.php Line: 478 Function: view File: /home/ah0ejbmyowku/public_html/application/controllers/Main.php Line: 107 Function: view File: /home/ah0ejbmyowku/public_html/index.php Line: 315 Function: require_once "> €4.95 ~~€ 9.90~~ / Notació_de_Coxeter" id="cancelSubscription" name="cancelSubscription" class="mb-0"> A PHP Error was encountered Severity: Notice Message: Undefined variable: user_membership Filename: user/popup_modal.php Line Number: 192 Backtrace: File: /home/ah0ejbmyowku/public_html/application/views/user/popup_modal.php Line: 192 Function: _error_handler File: /home/ah0ejbmyowku/public_html/application/views/page/index.php Line: 478 Function: view File: /home/ah0ejbmyowku/public_html/application/controllers/Main.php Line: 107 Function: view File: /home/ah0ejbmyowku/public_html/index.php Line: 315 Function: require_once A PHP Error was encountered Severity: Warning Message: Invalid argument supplied for foreach() Filename: user/popup_modal.php Line Number: 192 Backtrace: File: /home/ah0ejbmyowku/public_html/application/views/user/popup_modal.php Line: 192 Function: _error_handler File: /home/ah0ejbmyowku/public_html/application/views/page/index.php Line: 478 Function: view File: /home/ah0ejbmyowku/public_html/application/controllers/Main.php Line: 107 Function: view File: /home/ah0ejbmyowku/public_html/index.php Line: 315 Function: require_once A PHP Error was encountered Severity: Notice Message: Undefined variable: userid Filename: user/popup_modal.php Line Number: 208 Backtrace: File: /home/ah0ejbmyowku/public_html/application/views/user/popup_modal.php Line: 208 Function: _error_handler File: /home/ah0ejbmyowku/public_html/application/views/page/index.php Line: 478 Function: view File: /home/ah0ejbmyowku/public_html/application/controllers/Main.php Line: 107 Function: view File: /home/ah0ejbmyowku/public_html/index.php Line: 315 Function: require_once "> Harry Potter Books A PHP Error was encountered Severity: Notice Message: Undefined variable: products Filename: user/popup_harry_book.php Line Number: 24 Backtrace: File: /home/ah0ejbmyowku/public_html/application/views/user/popup_harry_book.php Line: 24 Function: _error_handler File: /home/ah0ejbmyowku/public_html/application/views/page/index.php Line: 479 Function: view File: /home/ah0ejbmyowku/public_html/application/controllers/Main.php Line: 107 Function: view File: /home/ah0ejbmyowku/public_html/index.php Line: 315 Function: require_once A PHP Error was encountered Severity: Warning Message: Invalid argument supplied for foreach() Filename: user/popup_harry_book.php Line Number: 24 Backtrace: File: /home/ah0ejbmyowku/public_html/application/views/user/popup_harry_book.php Line: 24 Function: _error_handler File: /home/ah0ejbmyowku/public_html/application/views/page/index.php Line: 479 Function: view File: /home/ah0ejbmyowku/public_html/application/controllers/Main.php Line: 107 Function: view File: /home/ah0ejbmyowku/public_html/index.php Line: 315 Function: require_once

[1]

[2]

[3]

[4]

[5]

[6]