Constructive Solid Geometry

Constructive Solid Geometry (CSG) oder konstruktive Festkörpergeometrie ist eine Technik zum Modellieren von Körpern, die u. a. in der 3D-Computergrafik und bei CAD-Programmen genutzt wird. Constructive Solid Geometry ermöglicht einem Designer einen komplex geformten Körper zu erzeugen, indem er boolesche Operatoren zur Kombination von Grundkörpern zu einem neuen Körper benutzt. Aus der CSG hervorgegangene Körper wirken oft sehr komplex, sind aber in Wirklichkeit nichts anderes als geschickt verknüpfte Objekte.

Die Basisobjekte, aus denen CSG-Körper hervorgehen, nennt man Primitive (vgl. Grafisches Primitiv). Typischerweise handelt es sich dabei um Körper, deren Oberfläche mittels einer relativ einfachen mathematischen Formel beschrieben werden kann, wie z. B. Würfel, Zylinder, Prismen, Pyramiden, Kugeln oder Ringe. Die Menge der möglichen Primitive wird gewöhnlich von der verwendeten Software begrenzt. Einige Software-Pakete erlauben CSG auf gekrümmten Objekten (prozedurale oder parametrische Oberflächen), während andere nur auf polygonalen Meshes (Dreiecksnetze) arbeiten. Der prozedurale oder parametrische Ansatz erlaubt eine mathematisch exakte Berechnung und Repräsentation der Körper, während Meshes immer nur eine mehr oder weniger ungenaue Annäherung an die Wirklichkeit sind.

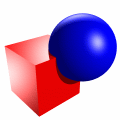
Wie bereits erwähnt, wird ein komplexer Körper von Primitiven erzeugt, die durch Operationen verknüpft sind. Gewöhnlich handelt es sich dabei um boolesche Operationen auf Mengen: Vereinigung (Union, ${\displaystyle \cup }$), Differenz (Difference, ${\displaystyle -}$) und Schnitt (Intersection, ${\displaystyle \cap }$). Folgende Abbildung zeigt die Wirkung der Operatoren exemplarisch an der Verknüpfung von Würfel mit Kugel:

• 
  Vereinigung: Zwei Objekte werden zu einem verschmolzen.
• 
  Differenz: Teile des zweiten Objekts werden aus dem ersten herausgeschnitten. Subtraktion (Würfel – Kugel).
• 
  Schnitt: Der Teil, den beide Objekte gemeinsam haben.

CSG ist unter Designern sehr beliebt, da man mit einer Anzahl relativ einfacher Körper komplexe Geometrien formen kann. Der Designer kann (bei den meisten Programmen) die Geometrie auch im Nachhinein noch ändern, indem er die Position (bzw. Transformation) der einzelnen Objekte oder den booleschen Operator ändert, mit dem die Objekte verbunden sind. Der Designer kann also sein Modell interaktiv und intuitiv, durch Versuch-und-Irrtum, kreieren.

CSG wird aber auch von diversen Programmen „unter der Haube“ benutzt, d. h. ohne, dass der Benutzer etwas von der Existenz der CSG-Operationen mitbekommt. So benutzen z. B. die Game-Engines von Unreal und Quake das CSG-Verfahren. Simulationsprogramme, die die Abläufe an Werkzeugmaschinen simulieren, verwenden i. d. R. ebenfalls CSG.

Da mehrere hintereinander ausgeführte CSG-Operationen im Allgemeinen nicht kommutativ sind, lassen sie sich hierarchisch ordnen und in einen CSG-Baum überführen. Jedes Blatt entspricht dabei einem Primitiv, jeder Knoten einer CSG-Operation (bzw. dem Zwischenergebnis aus einer CSG-Operation, welches wieder transformiert werden kann). Die Wurzel des Baumes ist das Endergebnis.

Die regularisierten Mengen des n-dimensionalen euklidischen Raumes bilden mit den Verknüpfungen ${\displaystyle \cup }$, ${\displaystyle \cap }$, ${\displaystyle c}$(Komplementärmenge) eine boolesche Algebra, für die auch das Kommutativgesetz gilt. Der ${\displaystyle \setminus }$-Operator ist nicht Teil dieser booleschen Algebra. Allerdings lassen sich der ${\displaystyle c}$- und ${\displaystyle \cap }$-Operator als Ersatz für den ${\displaystyle \setminus }$-Operator verwenden:

${\displaystyle A\setminus B\ =A\cap cB}$.

Das Beispielobjekt lässt sich von daher auch ohne Klammerung berechnen (${\displaystyle W}$ = Würfel, ${\displaystyle K}$ = Kugel, ${\displaystyle Z_{1},\ Z_{2},\ Z_{3}}$ = Zylinder):

${\displaystyle \mathrm {Resultat} =W\cap K\setminus (Z_{1}\cup Z_{2}\cup Z_{3})=W\cap K\cap cZ_{1}\cap cZ_{2}\cap cZ_{3}}$.

• Boundary Representation
• Convex Differences Aggregate
• Goldfeather-Algorithmus
• Solid modeling

• Christoph Martin Hoffmann: Geometric & Solid Modeling. Morgan Kaufmann Publishers, San Mateo, California 1989, ISBN 1-55860-067-1. 
• Martii Mäntylä: An Introduction to Solid Modeling. Computer Science Press, Rockville, Maryland 1988, ISBN 0-88175-108-1. 

• CSG-3MF Project - Open Source Bibliothek (GPL), C++, COM basiert mit C# Skript Unterstützung.
• GNU Triangulated Surface library – Open Source (LGPL) Bibliothek mit CSG-Unterstützung für Dreiecke
• Computational Geometry Algorithms Library – Open Source (LGPL, GPL) Bibliothek, welche unter anderem CSG unterstützt.
• The CSG rendering library – Open-Source-Bibliothek (GPL, Version 2) mit bildbasierenden CSG-Techniken via OpenGL.
• OpenSCAD – Ein einfaches CAD-Programm zur Erzeugung von 3D Objekten auf Basis von CSG.
• HyperFun Project – Eine einfache Skriptsprache um CSG-Operationen auf verschiedene Objekte anzuwenden.
• Overview of CSG in avoCADo – Open Source 3D-CAD-Software.
• SimpleGeo – Interaktiver CSG-Modeler für Monte-Carlo-Teilchentransport-Simulationen.
• FMEpedia CSGBuilder example – CSG mittels sogenannter FME (Feature Manipulation Engine).