Sinus versus (auch Sinusversus , Quersinus , Versinus oder Versus , in Formeln abgekürzt vers {\displaystyle \operatorname {vers} } Kosinus versus (auch Koversinus oder Querkosinus , in Formeln abgekürzt covers {\displaystyle \operatorname {covers} } Trigonometrie heute selten verwendete trigonometrische Funktionen . Semiversus (englisch haversine , in Formeln abgekürzt sem {\displaystyle \operatorname {sem} }
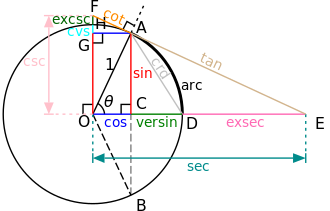
Veranschaulichung am Einheitskreis: C D {\displaystyle CD} O D {\displaystyle OD} G F {\displaystyle GF} O F {\displaystyle OF} Der Sinus versus wird mit Hilfe der Kosinus- oder Sinusfunktion definiert als[ 1]
vers θ = 1 − cos θ = 2 sin 2 θ 2 . {\displaystyle \operatorname {vers} \theta =1-\cos \theta =2\sin ^{2}{\frac {\theta }{2}}.} Er ist die Differenz des Kosinus zu +1 (in nebenstehender Abbildung in der Farbe Grün eingezeichnet).
Der Sinus versus kann auf die ganze komplexe Zahlenebene ausgeweitet werden.
Der Semiversus ist die Hälfte des Sinus versus:[ 2]
sem θ = vers θ 2 = sin 2 θ 2 {\displaystyle \operatorname {sem} \theta ={\frac {\operatorname {vers} \theta }{2}}=\sin ^{2}{\frac {\theta }{2}}} Der Kosinus versus ist in nebenstehender Abbildung in der Farbe Cyan und als cvs eingezeichnet.
covers θ = 1 − sin θ = vers ( π 2 − θ ) . {\displaystyle \operatorname {covers} \theta =1-\sin \theta =\operatorname {vers} \left({\frac {\pi }{2}}-\theta \right).} Er ist die Differenz des Sinus zu +1 und auch der Sinus versus des Gegenarguments (π/2 − θ ).[ 3]
Manchmal wird analog zu versin θ = 2 sin 2 ( θ / 2 ) {\displaystyle \operatorname {versin} \theta =2\sin ^{2}(\theta /2)} coversin θ = versin ( π / 2 − θ ) {\displaystyle \operatorname {coversin} \theta =\operatorname {versin} (\pi /2-\theta )}
versin θ = 1 − cos θ = 2 sin 2 θ 2 {\displaystyle \operatorname {versin} \theta =1-\cos \theta =2\sin ^{2}{\frac {\theta }{2}}} haversin θ = versin θ 2 = 1 − cos θ 2 {\displaystyle \operatorname {haversin} \theta ={\frac {\operatorname {versin} \theta }{2}}={\frac {1-\cos \theta }{2}}} vercos θ = 1 + cos θ = 2 cos 2 θ 2 {\displaystyle \operatorname {vercos} \theta =1+\cos \theta =2\cos ^{2}{\frac {\theta }{2}}} havercos θ = vercos θ 2 = 1 + cos θ 2 {\displaystyle \operatorname {havercos} \theta ={\frac {\operatorname {vercos} \theta }{2}}={\frac {1+\cos \theta }{2}}} coversin θ = 1 − sin θ = versin ( π 2 − θ ) {\displaystyle \operatorname {coversin} \theta =1-\sin \theta =\operatorname {versin} \left({\frac {\pi }{2}}-\theta \right)} hacoversin θ = coversin θ 2 = 1 − sin θ 2 {\displaystyle \operatorname {hacoversin} \theta ={\frac {\operatorname {coversin} \theta }{2}}={\frac {1-\sin \theta }{2}}} covercos θ = 1 + sin θ = vercos ( π 2 − θ ) {\displaystyle \operatorname {covercos} \theta =1+\sin \theta =\operatorname {vercos} \left({\frac {\pi }{2}}-\theta \right)} hacovercos θ = covercos θ 2 = 1 + sin θ 2 {\displaystyle \operatorname {hacovercos} \theta ={\frac {\operatorname {covercos} \theta }{2}}={\frac {1+\sin \theta }{2}}}
Die Ableitungen und die Stammfunktionen sind:
d d x versin x = sin x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {versin} x=\sin {x}} ∫ v e r s i n ( x ) d x = x − sin x + C {\displaystyle \int \mathrm {versin} (x)\,\mathrm {d} x=x-\sin {x}+C} d d x vercos x = − sin x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {vercos} x=-\sin {x}} ∫ v e r c o s ( x ) d x = x + sin x + C {\displaystyle \int \mathrm {vercos} (x)\,\mathrm {d} x=x+\sin {x}+C} d d x coversin x = − cos x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {coversin} x=-\cos {x}} ∫ c o v e r s i n ( x ) d x = x + cos x + C {\displaystyle \int \mathrm {coversin} (x)\,\mathrm {d} x=x+\cos {x}+C} d d x covercos x = cos x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {covercos} x=\cos {x}} ∫ c o v e r c o s ( x ) d x = x − cos x + C {\displaystyle \int \mathrm {covercos} (x)\,\mathrm {d} x=x-\cos {x}+C} d d x haversin x = sin x 2 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {haversin} x={\frac {\sin {x}}{2}}} ∫ h a v e r s i n ( x ) d x = x − sin x 2 + C {\displaystyle \int \mathrm {haversin} (x)\,\mathrm {d} x={\frac {x-\sin {x}}{2}}+C} d d x havercos x = − sin x 2 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {havercos} x={\frac {-\sin {x}}{2}}} ∫ h a v e r c o s ( x ) d x = x + sin x 2 + C {\displaystyle \int \mathrm {havercos} (x)\,\mathrm {d} x={\frac {x+\sin {x}}{2}}+C} d d x hacoversin x = − cos x 2 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {hacoversin} x={\frac {-\cos {x}}{2}}} ∫ h a c o v e r s i n ( x ) d x = x + cos x 2 + C {\displaystyle \int \mathrm {hacoversin} (x)\,\mathrm {d} x={\frac {x+\cos {x}}{2}}+C} d d x hacovercos x = cos x 2 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {hacovercos} x={\frac {\cos {x}}{2}}} ∫ h a c o v e r c o s ( x ) d x = x − cos x 2 + C {\displaystyle \int \mathrm {hacovercos} (x)\,\mathrm {d} x={\frac {x-\cos {x}}{2}}+C}
Der Seiten-Kosinussatz der sphärischen Trigonometrie spielte für die nautische Navigation nach den Sternen in früherer Zeit eine wichtige Rolle.[ 4] [ 5]
Es ergibt sich daraus unter anderem damit der Seiten-Kosinussatz zu:
s e m ( a ) = s e m ( b − c ) + sin ( b ) ⋅ sin ( c ) ⋅ s e m ( α ) {\displaystyle {\rm {sem}}(a)={\rm {sem}}(b-c)+\sin(b)\cdot \sin(c)\cdot {\rm {sem}}(\alpha )} ↑ Eric W. Weisstein : Versine .MathWorld ↑ Eric W. Weisstein : Haversine .MathWorld ↑ Eric W. Weisstein : Coversine .MathWorld ↑ Bobby Schenk: Astronavigation: ohne Formeln - praxisnah . 2. Auflage. Delius Klasing & Co., Bielefeld 1978. ↑ Otto Fulst: Nautische Tafeln . Hrsg.: Johannes Lütjen, Walter Stein, Gerhard Zwiebler. 24. Auflage. Arthur Geist Verlag, Bremen 1972, 17–18.  Van Wikipedia, de gratis encyclopedie
Van Wikipedia, de gratis encyclopedie