17 equal temperament

From Wikipedia the free encyclopedia

Figure 1: 17-ET on the regular diatonic tuning continuum at P5=705.88 cents.[1]
1 step in 17-ET

In music, 17 equal temperament is the tempered scale derived by dividing the octave into 17 equal steps (equal frequency ratios). Each step represents a frequency ratio of 17√2, or 70.6 cents.

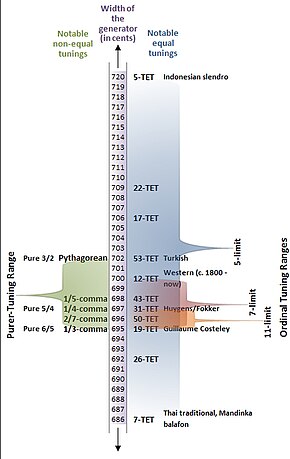
17-ET is the tuning of the regular diatonic tuning in which the tempered perfect fifth is equal to 705.88 cents, as shown in Figure 1 (look for the label "17-TET").

History and use

[edit]

Alexander J. Ellis refers to a tuning of seventeen tones based on perfect fourths and fifths as the Arabic scale.[2] In the thirteenth century, Middle-Eastern musician Safi al-Din Urmawi developed a theoretical system of seventeen tones to describe Arabic and Persian music, although the tones were not equally spaced. This 17-tone system remained the primary theoretical system until the development of the quarter tone scale.[citation needed]

Notation

[edit]
Notation of Easley Blackwood[3] for 17 equal temperament: intervals are notated similarly to those they approximate and enharmonic equivalents are distinct from those of 12 equal temperament (e.g., A♯/C♭).

Easley Blackwood Jr. created a notation system where sharps and flats raised/lowered 2 steps. This yields the chromatic scale:

C, D♭, C♯, D, E♭, D♯, E, F, G♭, F♯, G, A♭, G♯, A, B♭, A♯, B, C

Quarter tone sharps and flats can also be used, yielding the following chromatic scale:

C, Chalf sharp/D♭, C♯/Dhalf flat, D, Dhalf sharp/E♭, D♯/Ehalf flat, E, F, Fhalf sharp/G♭, F♯/Ghalf flat, G, Ghalf sharp/A♭, G♯/Ahalf flat, A, Ahalf sharp/B♭, A♯/Bhalf flat, B, C

Interval size

[edit]

Below are some intervals in 17-EDO compared to just.

Major chord on C in 17 equal temperament: all notes within 37 cents of just intonation (rather than 14 for 12 equal temperament)
17-et
just
12-et
I–IV–V–I chord progression in 17 equal temperament.[4] Whereas in 12-EDO, B♮ is 11 steps, in 17-EDO B♮ is 16 steps.
interval name size (steps) size (cents) midi just ratio just (cents) midi error
octave 17 1200 2:1 1200 0
minor seventh 14 988.23 16:9 996 −07.77
perfect fifth 10 705.88 3:2 701.96 +03.93
septimal tritone 08 564.71 7:5 582.51 −17.81
tridecimal narrow tritone 08 564.71 18:13 563.38 +01.32
undecimal super-fourth 08 564.71 11:80 551.32 +13.39
perfect fourth 07 494.12 4:3 498.04 −03.93
septimal major third 06 423.53 9:7 435.08 −11.55
undecimal major third 06 423.53 14:11 417.51 +06.02
major third 05 352.94 5:4 386.31 −33.37
tridecimal neutral third 05 352.94 16:13 359.47 −06.53
undecimal neutral third 05 352.94 11:90 347.41 +05.53
minor third 04 282.35 6:5 315.64 −33.29
tridecimal minor third 04 282.35 13:11 289.21 −06.86
septimal minor third 04 282.35 7:6 266.87 +15.48
septimal whole tone 03 211.76 8:7 231.17 −19.41
whole tone 03 211.76 9:8 203.91 +07.85
neutral second, lesser undecimal 02 141.18 12:11 150.64 −09.46
greater tridecimal 2⁄3-tone 02 141.18 13:12 138.57 +02.60
lesser tridecimal 2⁄3-tone 02 141.18 14:13 128.30 +12.88
septimal diatonic semitone 02 141.18 15:14 119.44 +21.73
diatonic semitone 02 141.18 16:15 111.73 +29.45
septimal chromatic semitone 01 070.59 21:20 084.47 −13.88
chromatic semitone 01 070.59 25:24 070.67 −00.08

Relation to 34-ET

[edit]

17-ET is where every other step in the 34-ET scale is included, and the others are not accessible. Conversely 34-ET is a subdivision of 17-ET.

References

[edit]
  1. ^ Milne, Sethares & Plamondon 2007, pp. 15–32.
  2. ^ Ellis, Alexander J. (1863). "On the Temperament of Musical Instruments with Fixed Tones", Proceedings of the Royal Society of London, vol. 13. (1863–1864), pp. 404–422.
  3. ^ Blackwood, Easley (Summer 1991). "Modes and Chord Progressions in Equal Tunings". Perspectives of New Music. 29 (2): 166–200 (175). doi:10.2307/833437. JSTOR 833437.
  4. ^ Milne, Sethares & Plamondon 2007, p. 29.

Sources

[edit]
Retrieved from "https://en.wikipedia.org/w/index.php?title=17_equal_temperament&oldid=1192926979"