Diffusion MRI
 From Wikipedia the free encyclopedia
From Wikipedia the free encyclopedia
| Diffusion MRI | |
|---|---|
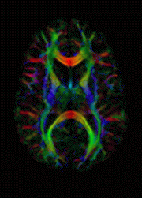 DTI Color Map | |
| MeSH | D038524 |
Diffusion-weighted magnetic resonance imaging (DWI or DW-MRI) is the use of specific MRI sequences as well as software that generates images from the resulting data that uses the diffusion of water molecules to generate contrast in MR images.[1][2][3] It allows the mapping of the diffusion process of molecules, mainly water, in biological tissues, in vivo and non-invasively. Molecular diffusion in tissues is not random, but reflects interactions with many obstacles, such as macromolecules, fibers, and membranes. Water molecule diffusion patterns can therefore reveal microscopic details about tissue architecture, either normal or in a diseased state. A special kind of DWI, diffusion tensor imaging (DTI), has been used extensively to map white matter tractography in the brain.
Introduction
[edit]In diffusion weighted imaging (DWI), the intensity of each image element (voxel) reflects the best estimate of the rate of water diffusion at that location. Because the mobility of water is driven by thermal agitation and highly dependent on its cellular environment, the hypothesis behind DWI is that findings may indicate (early) pathologic change. For instance, DWI is more sensitive to early changes after a stroke than more traditional MRI measurements such as T1 or T2 relaxation rates. A variant of diffusion weighted imaging, diffusion spectrum imaging (DSI),[4] was used in deriving the Connectome data sets; DSI is a variant of diffusion-weighted imaging that is sensitive to intra-voxel heterogeneities in diffusion directions caused by crossing fiber tracts and thus allows more accurate mapping of axonal trajectories than other diffusion imaging approaches.[5]
Diffusion-weighted images are very useful to diagnose vascular strokes in the brain. It is also used more and more in the staging of non-small-cell lung cancer, where it is a serious candidate to replace positron emission tomography as the 'gold standard' for this type of disease. Diffusion tensor imaging is being developed for studying the diseases of the white matter of the brain as well as for studies of other body tissues (see below). DWI is most applicable when the tissue of interest is dominated by isotropic water movement e.g. grey matter in the cerebral cortex and major brain nuclei, or in the body—where the diffusion rate appears to be the same when measured along any axis. However, DWI also remains sensitive to T1 and T2 relaxation. To entangle diffusion and relaxation effects on image contrast, one may obtain quantitative images of the diffusion coefficient, or more exactly the apparent diffusion coefficient (ADC). The ADC concept was introduced to take into account the fact that the diffusion process is complex in biological tissues and reflects several different mechanisms.[6]
Diffusion tensor imaging (DTI) is important when a tissue—such as the neural axons of white matter in the brain or muscle fibers in the heart—has an internal fibrous structure analogous to the anisotropy of some crystals. Water will then diffuse more rapidly in the direction aligned with the internal structure (axial diffusion), and more slowly as it moves perpendicular to the preferred direction (radial diffusion). This also means that the measured rate of diffusion will differ depending on the direction from which an observer is looking.
Diffusion Basis Spectrum Imaging (DBSI) further separates DTI signals into discrete anisotropic diffusion tensors and a spectrum of isotropic diffusion tensors to better differentiate sub-voxel cellular structures. For example, anisotropic diffusion tensors correlate to axonal fibers, while low isotropic diffusion tensors correlate to cells and high isotropic diffusion tensors correlate to larger structures (such as the lumen or brain ventricles).[7] DBSI has been shown to differentiate some types of brain tumors and multiple sclerosis with higher specificity and sensitivity than conventional DTI.[8][9][10][11] DBSI has also been useful in determining microstructure properties of the brain.[12]
Traditionally, in diffusion-weighted imaging (DWI), three gradient-directions are applied, sufficient to estimate the trace of the diffusion tensor or 'average diffusivity', a putative measure of edema. Clinically, trace-weighted images have proven to be very useful to diagnose vascular strokes in the brain, by early detection (within a couple of minutes) of the hypoxic edema.[13]
More extended DTI scans derive neural tract directional information from the data using 3D or multidimensional vector algorithms based on six or more gradient directions, sufficient to compute the diffusion tensor. The diffusion tensor model is a rather simple model of the diffusion process, assuming homogeneity and linearity of the diffusion within each image voxel.[13] From the diffusion tensor, diffusion anisotropy measures such as the fractional anisotropy (FA), can be computed. Moreover, the principal direction of the diffusion tensor can be used to infer the white-matter connectivity of the brain (i.e. tractography; trying to see which part of the brain is connected to which other part).
Recently, more advanced models of the diffusion process have been proposed that aim to overcome the weaknesses of the diffusion tensor model. Amongst others, these include q-space imaging [14] and generalized diffusion tensor imaging.
Mechanism
[edit]Diffusion imaging is an MRI method that produces in vivo magnetic resonance images of biological tissues sensitized with the local characteristics of molecular diffusion, generally water (but other moieties can also be investigated using MR spectroscopic approaches).[15] MRI can be made sensitive to the motion of molecules. Regular MRI acquisition utilizes the behavior of protons in water to generate contrast between clinically relevant features of a particular subject. The versatile nature of MRI is due to this capability of producing contrast related to the structure of tissues at the microscopic level. In a typical -weighted image, water molecules in a sample are excited with the imposition of a strong magnetic field. This causes many of the protons in water molecules to precess simultaneously, producing signals in MRI. In -weighted images, contrast is produced by measuring the loss of coherence or synchrony between the water protons. When water is in an environment where it can freely tumble, relaxation tends to take longer. In certain clinical situations, this can generate contrast between an area of pathology and the surrounding healthy tissue.
To sensitize MRI images to diffusion, the magnetic field strength (B1) is varied linearly by a pulsed field gradient. Since precession is proportional to the magnet strength, the protons begin to precess at different rates, resulting in dispersion of the phase and signal loss. Another gradient pulse is applied in the same magnitude but with opposite direction to refocus or rephase the spins. The refocusing will not be perfect for protons that have moved during the time interval between the pulses, and the signal measured by the MRI machine is reduced. This "field gradient pulse" method was initially devised for NMR by Stejskal and Tanner [16] who derived the reduction in signal due to the application of the pulse gradient related to the amount of diffusion that is occurring through the following equation:
where is the signal intensity without the diffusion weighting, is the signal with the gradient, is the gyromagnetic ratio, is the strength of the gradient pulse, is the duration of the pulse, is the time between the two pulses, and finally, is the diffusion-coefficient.
In order to localize this signal attenuation to get images of diffusion one has to combine the pulsed magnetic field gradient pulses used for MRI (aimed at localization of the signal, but those gradient pulses are too weak to produce a diffusion related attenuation) with additional "motion-probing" gradient pulses, according to the Stejskal and Tanner method. This combination is not trivial, as cross-terms arise between all gradient pulses. The equation set by Stejskal and Tanner then becomes inaccurate and the signal attenuation must be calculated, either analytically or numerically, integrating all gradient pulses present in the MRI sequence and their interactions. The result quickly becomes very complex given the many pulses present in the MRI sequence, and as a simplification, Le Bihan suggested gathering all the gradient terms in a "b factor" (which depends only on the acquisition parameters) so that the signal attenuation simply becomes:[1]
Also, the diffusion coefficient, , is replaced by an apparent diffusion coefficient, , to indicate that the diffusion process is not free in tissues, but hindered and modulated by many mechanisms (restriction in closed spaces, tortuosity around obstacles, etc.) and that other sources of IntraVoxel Incoherent Motion (IVIM) such as blood flow in small vessels or cerebrospinal fluid in ventricles also contribute to the signal attenuation. At the end, images are "weighted" by the diffusion process: In those diffusion-weighted images (DWI) the signal is more attenuated the faster the diffusion and the larger the b factor is. However, those diffusion-weighted images are still also sensitive to T1 and T2 relaxivity contrast, which can sometimes be confusing. It is possible to calculate "pure" diffusion maps (or more exactly ADC maps where the ADC is the sole source of contrast) by collecting images with at least 2 different values, and , of the b factor according to:
Although this ADC concept has been extremely successful, especially for clinical applications, it has been challenged recently, as new, more comprehensive models of diffusion in biological tissues have been introduced. Those models have been made necessary, as diffusion in tissues is not free. In this condition, the ADC seems to depend on the choice of b values (the ADC seems to decrease when using larger b values), as the plot of ln(S/So) is not linear with the b factor, as expected from the above equations. This deviation from a free diffusion behavior is what makes diffusion MRI so successful, as the ADC is very sensitive to changes in tissue microstructure. On the other hand, modeling diffusion in tissues is becoming very complex. Among most popular models are the biexponential model, which assumes the presence of 2 water pools in slow or intermediate exchange [17][18] and the cumulant-expansion (also called Kurtosis) model,[19][20][21] which does not necessarily require the presence of 2 pools.
Diffusion model
[edit]Given the concentration and flux , Fick's first law gives a relationship between the flux and the concentration gradient:
where D is the diffusion coefficient. Then, given conservation of mass, the continuity equation relates the time derivative of the concentration with the divergence of the flux:
Putting the two together, we get the diffusion equation:
Magnetization dynamics
[edit]With no diffusion present, the change in nuclear magnetization over time is given by the classical Bloch equation
which has terms for precession, T2 relaxation, and T1 relaxation.
In 1956, H.C. Torrey mathematically showed how the Bloch equations for magnetization would change with the addition of diffusion.[22] Torrey modified Bloch's original description of transverse magnetization to include diffusion terms and the application of a spatially varying gradient. Since the magnetization is a vector, there are 3 diffusion equations, one for each dimension. The Bloch-Torrey equation is:
where is now the diffusion tensor.
For the simplest case where the diffusion is isotropic the diffusion tensor is a multiple of the identity:
then the Bloch-Torrey equation will have the solution
The exponential term will be referred to as the attenuation . Anisotropic diffusion will have a similar solution for the diffusion tensor, except that what will be measured is the apparent diffusion coefficient (ADC). In general, the attenuation is:
where the terms incorporate the gradient fields , , and .
Grayscale
[edit]The standard grayscale of DWI images is to represent increased diffusion restriction as brighter.[23]
ADC image
[edit]
An apparent diffusion coefficient (ADC) image, or an ADC map, is an MRI image that more specifically shows diffusion than conventional DWI, by eliminating the T2 weighting that is otherwise inherent to conventional DWI.[24][25] ADC imaging does so by acquiring multiple conventional DWI images with different amounts of DWI weighting, and the change in signal is proportional to the rate of diffusion. Contrary to DWI images, the standard grayscale of ADC images is to represent a smaller magnitude of diffusion as darker.[23]
Cerebral infarction leads to diffusion restriction, and the difference between images with various DWI weighting will therefore be minor, leading to an ADC image with low signal in the infarcted area.[24] A decreased ADC may be detected minutes after a cerebral infarction.[26] The high signal of infarcted tissue on conventional DWI is a result of its partial T2 weighting.[27]
Diffusion tensor imaging
[edit]Diffusion tensor imaging (DTI) is a magnetic resonance imaging technique that enables the measurement of the restricted diffusion of water in tissue in order to produce neural tract images instead of using this data solely for the purpose of assigning contrast or colors to pixels in a cross-sectional image. It also provides useful structural information about muscle—including heart muscle—as well as other tissues such as the prostate.[28]
In DTI, each voxel has one or more pairs of parameters: a rate of diffusion and a preferred direction of diffusion—described in terms of three-dimensional space—for which that parameter is valid. The properties of each voxel of a single DTI image are usually calculated by vector or tensor math from six or more different diffusion weighted acquisitions, each obtained with a different orientation of the diffusion sensitizing gradients. In some methods, hundreds of measurements—each making up a complete image—are made to generate a single resulting calculated image data set. The higher information content of a DTI voxel makes it extremely sensitive to subtle pathology in the brain. In addition the directional information can be exploited at a higher level of structure to select and follow neural tracts through the brain—a process called tractography.[29]
A more precise statement of the image acquisition process is that the image-intensities at each position are attenuated, depending on the strength (b-value) and direction of the so-called magnetic diffusion gradient, as well as on the local microstructure in which the water molecules diffuse. The more attenuated the image is at a given position, the greater diffusion there is in the direction of the diffusion gradient. In order to measure the tissue's complete diffusion profile, one needs to repeat the MR scans, applying different directions (and possibly strengths) of the diffusion gradient for each scan.
Mathematical foundation—tensors
[edit]Diffusion MRI relies on the mathematics and physical interpretations of the geometric quantities known as tensors. Only a special case of the general mathematical notion is relevant to imaging, which is based on the concept of a symmetric matrix.[notes 1] Diffusion itself is tensorial, but in many cases the objective is not really about trying to study brain diffusion per se, but rather just trying to take advantage of diffusion anisotropy in white matter for the purpose of finding the orientation of the axons and the magnitude or degree of anisotropy. Tensors have a real, physical existence in a material or tissue so that they do not move when the coordinate system used to describe them is rotated. There are numerous different possible representations of a tensor (of rank 2), but among these, this discussion focuses on the ellipsoid because of its physical relevance to diffusion and because of its historical significance in the development of diffusion anisotropy imaging in MRI.
The following matrix displays the components of the diffusion tensor:
The same matrix of numbers can have a simultaneous second use to describe the shape and orientation of an ellipse and the same matrix of numbers can be used simultaneously in a third way for matrix mathematics to sort out eigenvectors and eigenvalues as explained below.
Physical tensors
[edit]The idea of a tensor in physical science evolved from attempts to describe the quantity of physical properties. The first properties they were applied to were those that can be described by a single number, such as temperature. Properties that can be described this way are called scalars; these can be considered tensors of rank 0, or 0th-order tensors. Tensors can also be used to describe quantities that have directionality, such as mechanical force. These quantities require specification of both magnitude and direction, and are often represented with a vector. A three-dimensional vector can be described with three components: its projection on the x, y, and z axes. Vectors of this sort can be considered tensors of rank 1, or 1st-order tensors.
A tensor is often a physical or biophysical property that determines the relationship between two vectors. When a force is applied to an object, movement can result. If the movement is in a single direction, the transformation can be described using a vector—a tensor of rank 1. However, in a tissue, diffusion leads to movement of water molecules along trajectories that proceed along multiple directions over time, leading to a complex projection onto the Cartesian axes. This pattern is reproducible if the same conditions and forces are applied to the same tissue in the same way. If there is an internal anisotropic organization of the tissue that constrains diffusion, then this fact will be reflected in the pattern of diffusion. The relationship between the properties of driving force that generate diffusion of the water molecules and the resulting pattern of their movement in the tissue can be described by a tensor. The collection of molecular displacements of this physical property can be described with nine components—each one associated with a pair of axes xx, yy, zz, xy, yx, xz, zx, yz, zy.[30] These can be written as a matrix similar to the one at the start of this section.
Diffusion from a point source in the anisotropic medium of white matter behaves in a similar fashion. The first pulse of the Stejskal Tanner diffusion gradient effectively labels some water molecules and the second pulse effectively shows their displacement due to diffusion. Each gradient direction applied measures the movement along the direction of that gradient. Six or more gradients are summed to get all the measurements needed to fill in the matrix, assuming it is symmetric above and below the diagonal (red subscripts).
In 1848, Henri Hureau de Sénarmont[31] applied a heated point to a polished crystal surface that had been coated with wax. In some materials that had "isotropic" structure, a ring of melt would spread across the surface in a circle. In anisotropic crystals the spread took the form of an ellipse. In three dimensions this spread is an ellipsoid. As Adolf Fick showed in the 1850s, diffusion exhibits many of the same patterns as those seen in the transfer of heat.
Mathematics of ellipsoids
[edit]At this point, it is helpful to consider the mathematics of ellipsoids. An ellipsoid can be described by the formula: . This equation describes a quadric surface. The relative values of a, b, and c determine if the quadric describes an ellipsoid or a hyperboloid.
As it turns out, three more components can be added as follows: . Many combinations of a, b, c, d, e, and f still describe ellipsoids, but the additional components (d, e, f) describe the rotation of the ellipsoid relative to the orthogonal axes of the Cartesian coordinate system. These six variables can be represented by a matrix similar to the tensor matrix defined at the start of this section (since diffusion is symmetric, then we only need six instead of nine components—the components below the diagonal elements of the matrix are the same as the components above the diagonal). This is what is meant when it is stated that the components of a matrix of a second order tensor can be represented by an ellipsoid—if the diffusion values of the six terms of the quadric ellipsoid are placed into the matrix, this generates an ellipsoid angled off the orthogonal grid. Its shape will be more elongated if the relative anisotropy is high.
When the ellipsoid/tensor is represented by a matrix, we can apply a useful technique from standard matrix mathematics and linear algebra—that is to "diagonalize" the matrix. This has two important meanings in imaging. The idea is that there are two equivalent ellipsoids—of identical shape but with different size and orientation. The first one is the measured diffusion ellipsoid sitting at an angle determined by the axons, and the second one is perfectly aligned with the three Cartesian axes. The term "diagonalize" refers to the three components of the matrix along a diagonal from upper left to lower right (the components with red subscripts in the matrix at the start of this section). The variables , , and are along the diagonal (red subscripts), but the variables d, e and f are "off diagonal". It then becomes possible to do a vector processing step in which we rewrite our matrix and replace it with a new matrix multiplied by three different vectors of unit length (length=1.0). The matrix is diagonalized because the off-diagonal components are all now zero. The rotation angles required to get to this equivalent position now appear in the three vectors and can be read out as the x, y, and z components of each of them. Those three vectors are called "eigenvectors" or characteristic vectors. They contain the orientation information of the original ellipsoid. The three axes of the ellipsoid are now directly along the main orthogonal axes of the coordinate system so we can easily infer their lengths. These lengths are the eigenvalues or characteristic values.
Diagonalization of a matrix is done by finding a second matrix that it can be multiplied with followed by multiplication by the inverse of the second matrix—wherein the result is a new matrix in which three diagonal (xx, yy, zz) components have numbers in them but the off-diagonal components (xy, yz, zx) are 0. The second matrix provides eigenvector information.
Measures of anisotropy and diffusivity
[edit]
In present-day clinical neurology, various brain pathologies may be best detected by looking at particular measures of anisotropy and diffusivity. The underlying physical process of diffusion causes a group of water molecules to move out from a central point, and gradually reach the surface of an ellipsoid if the medium is anisotropic (it would be the surface of a sphere for an isotropic medium). The ellipsoid formalism functions also as a mathematical method of organizing tensor data. Measurement of an ellipsoid tensor further permits a retrospective analysis, to gather information about the process of diffusion in each voxel of the tissue.[32]
In an isotropic medium such as cerebrospinal fluid, water molecules are moving due to diffusion and they move at equal rates in all directions. By knowing the detailed effects of diffusion gradients we can generate a formula that allows us to convert the signal attenuation of an MRI voxel into a numerical measure of diffusion—the diffusion coefficient D. When various barriers and restricting factors such as cell membranes and microtubules interfere with the free diffusion, we are measuring an "apparent diffusion coefficient", or ADC, because the measurement misses all the local effects and treats the attenuation as if all the movement rates were solely due to Brownian motion. The ADC in anisotropic tissue varies depending on the direction in which it is measured. Diffusion is fast along the length of (parallel to) an axon, and slower perpendicularly across it.
Once we have measured the voxel from six or more directions and corrected for attenuations due to T2 and T1 effects, we can use information from our calculated ellipsoid tensor to describe what is happening in the voxel. If you consider an ellipsoid sitting at an angle in a Cartesian grid then you can consider the projection of that ellipse onto the three axes. The three projections can give you the ADC along each of the three axes ADCx, ADCy, ADCz. This leads to the idea of describing the average diffusivity in the voxel which will simply be
We use the i subscript to signify that this is what the isotropic diffusion coefficient would be with the effects of anisotropy averaged out.
The ellipsoid itself has a principal long axis and then two more small axes that describe its width and depth. All three of these are perpendicular to each other and cross at the center point of the ellipsoid. We call the axes in this setting eigenvectors and the measures of their lengths eigenvalues. The lengths are symbolized by the Greek letter λ. The long one pointing along the axon direction will be λ1 and the two small axes will have lengths λ2 and λ3. In the setting of the DTI tensor ellipsoid, we can consider each of these as a measure of the diffusivity along each of the three primary axes of the ellipsoid. This is a little different from the ADC since that was a projection on the axis, while λ is an actual measurement of the ellipsoid we have calculated.
The diffusivity along the principal axis, λ1 is also called the longitudinal diffusivity or the axial diffusivity or even the parallel diffusivity λ∥. Historically, this is closest to what Richards originally measured with the vector length in 1991.[33] The diffusivities in the two minor axes are often averaged to produce a measure of radial diffusivity
This quantity is an assessment of the degree of restriction due to membranes and other effects and proves to be a sensitive measure of degenerative pathology in some neurological conditions.[34] It can also be called the perpendicular diffusivity ().
Another commonly used measure that summarizes the total diffusivity is the Trace—which is the sum of the three eigenvalues,
where is a diagonal matrix with eigenvalues , and on its diagonal.
If we divide this sum by three we have the mean diffusivity,
which equals ADCi since
where is the matrix of eigenvectors and is the diffusion tensor. Aside from describing the amount of diffusion, it is often important to describe the relative degree of anisotropy in a voxel. At one extreme would be the sphere of isotropic diffusion and at the other extreme would be a cigar or pencil shaped very thin prolate spheroid. The simplest measure is obtained by dividing the longest axis of the ellipsoid by the shortest = (λ1/λ3). However, this proves to be very susceptible to measurement noise, so increasingly complex measures were developed to capture the measure while minimizing the noise. An important element of these calculations is the sum of squares of the diffusivity differences = (λ1 − λ2)2 + (λ1 − λ3)2 + (λ2 − λ3)2. We use the square root of the sum of squares to obtain a sort of weighted average—dominated by the largest component. One objective is to keep the number near 0 if the voxel is spherical but near 1 if it is elongate. This leads to the fractional anisotropy or FA which is the square root of the sum of squares (SRSS) of the diffusivity differences, divided by the SRSS of the diffusivities. When the second and third axes are small relative to the principal axis, the number in the numerator is almost equal the number in the denominator. We also multiply by so that FA has a maximum value of 1. The whole formula for FA looks like this:
where
The fractional anisotropy can also be separated into linear, planar, and spherical measures depending on the "shape" of the diffusion ellipsoid.[35][36] For example, a "cigar" shaped prolate ellipsoid indicates a strongly linear anisotropy, a "flying saucer" or oblate spheroid represents diffusion in a plane, and a sphere is indicative of isotropic diffusion, equal in all directions.[37] If the eigenvalues of the diffusion vector are sorted such that , then the measures can be calculated as follows:
For the linear case, where ,
For the planar case, where ,
For the spherical case, where ,
Each measure lies between 0 and 1 and they sum to unity. An additional anisotropy measure can used to describe the deviation from the spherical case:
There are other metrics of anisotropy used, including the relative anisotropy (RA):
and the volume ratio (VR):
Applications
[edit]This section needs additional citations for verification. (December 2013) |
The most common application of conventional DWI (without DTI) is in acute brain ischemia. DWI directly visualizes the ischemic necrosis in cerebral infarction in the form of a cytotoxic edema,[38] appearing as a high DWI signal within minutes of arterial occlusion.[39] With perfusion MRI detecting both the infarcted core and the salvageable penumbra, the latter can be quantified by DWI and perfusion MRI.[40]
- DWI showing necrosis (shown as brighter) in a cerebral infarction
- DWI showing restricted diffusion in the medial dorsal thalami consistent with Wernicke encephalopathy
- DWI showing cortical ribbon-like high signal consistent with diffusion restriction in a patient with known MELAS syndrome
Another application area of DWI is in oncology. Tumors are in many instances highly cellular, giving restricted diffusion of water, and therefore appear with a relatively high signal intensity in DWI.[41] DWI is commonly used to detect and stage tumors, and also to monitor tumor response to treatment over time. DWI can also be collected to visualize the whole body using a technique called 'diffusion-weighted whole-body imaging with background body signal suppression' (DWIBS).[42] Some more specialized diffusion MRI techniques such as diffusion kurtosis imaging (DKI) have also been shown to predict the response of cancer patients to chemotherapy treatment.[43]
The principal application is in the imaging of white matter where the location, orientation, and anisotropy of the tracts can be measured. The architecture of the axons in parallel bundles, and their myelin sheaths, facilitate the diffusion of the water molecules preferentially along their main direction. Such preferentially oriented diffusion is called anisotropic diffusion.


The imaging of this property is an extension of diffusion MRI. If a series of diffusion gradients (i.e. magnetic field variations in the MRI magnet) are applied that can determine at least 3 directional vectors (use of 6 different gradients is the minimum and additional gradients improve the accuracy for "off-diagonal" information), it is possible to calculate, for each voxel, a tensor (i.e. a symmetric positive definite 3×3 matrix) that describes the 3-dimensional shape of diffusion. The fiber direction is indicated by the tensor's main eigenvector. This vector can be color-coded, yielding a cartography of the tracts' position and direction (red for left-right, blue for superior-inferior, and green for anterior-posterior).[45] The brightness is weighted by the fractional anisotropy which is a scalar measure of the degree of anisotropy in a given voxel. Mean diffusivity (MD) or trace is a scalar measure of the total diffusion within a voxel. These measures are commonly used clinically to localize white matter lesions that do not show up on other forms of clinical MRI.[46]
Applications in the brain:
- Tract-specific localization of white matter lesions such as trauma and in defining the severity of diffuse traumatic brain injury. The localization of tumors in relation to the white matter tracts (infiltration, deflection), has been one of the most important initial applications. In surgical planning for some types of brain tumors, surgery is aided by knowing the proximity and relative position of the corticospinal tract and a tumor.
- Diffusion tensor imaging data can be used to perform tractography within white matter. Fiber tracking algorithms can be used to track a fiber along its whole length (e.g. the corticospinal tract, through which the motor information transit from the motor cortex to the spinal cord and the peripheral nerves). Tractography is a useful tool for measuring deficits in white matter, such as in aging. Its estimation of fiber orientation and strength is increasingly accurate, and it has widespread potential implications in the fields of cognitive neuroscience and neurobiology.
- The use of DTI for the assessment of white matter in development, pathology and degeneration has been the focus of over 2,500 research publications since 2005. It promises to be very helpful in distinguishing Alzheimer's disease from other types of dementia. Applications in brain research include the investigation of neural networks in vivo, as well as in connectomics.
Applications for peripheral nerves:
- Brachial plexus: DTI can differentiate normal nerves[47] (as shown in the tractogram of the spinal cord and brachial plexus and 3D 4k reconstruction here) from traumatically injured nerve roots.[44]
- Cubital Tunnel Syndrome: metrics derived from DTI (FA and RD) can differentiate asymptomatic adults from those with compression of the ulnar nerve at the elbow[48]
- Carpal Tunnel Syndrome: Metrics derived from DTI (lower FA and MD) differentiate healthy adults from those with carpal tunnel syndrome[49]
Research
[edit]Early in the development of DTI based tractography, a number of researchers pointed out a flaw in the diffusion tensor model. The tensor analysis assumes that there is a single ellipsoid in each imaging voxel—as if all of the axons traveling through a voxel traveled in exactly the same direction.[50] This is often true, but it can be estimated that in more than 30% of the voxels in a standard resolution brain image, there are at least two different neural tracts traveling in different directions that pass through each other. In the classic diffusion ellipsoid tensor model, the information from the crossing tract appears as noise or unexplained decreased anisotropy in a given voxel.
David Tuch was among the first to describe a solution to this problem.[51][52] The idea is best understood by conceptually placing a kind of geodesic dome around each image voxel. This icosahedron provides a mathematical basis for passing a large number of evenly spaced gradient trajectories through the voxel—each coinciding with one of the apices of the icosahedron. We can then look into the voxel from a large number of different directions (typically 40 or more). We use "n-tuple" tessellations to add more evenly spaced apices to the original icosahedron (20 faces)—an idea that also had its precedents in paleomagnetism research several decades earlier.[53] We want to know which direction lines turn up the maximum anisotropic diffusion measures. If there is a single tract, there will be only two maxima, pointing in opposite directions. If two tracts cross in the voxel, there will be two pairs of maxima, and so on. We can still use tensor mathematics to use the maxima to select groups of gradients to package into several different tensor ellipsoids in the same voxel, or use more complex higher-rank tensor analyses,[54] or we can do a true "model free" analysis that picks the maxima, and then continue to do the tractography.
The Q-Ball method of tractography is an implementation in which David Tuch provides a mathematical alternative to the tensor model.[50] Instead of forcing the diffusion anisotropy data into a group of tensors, the mathematics used deploys both probability distributions and some classic geometric tomography and vector mathematics developed nearly 100 years ago—the Funk Radon Transform.[55]
Note, there is ongoing debate about the best way to preprocess DW-MRI. Several in-vivo studies have shown that the choice of software and functions applied (directed at correcting artefacts arising from e.g. motion and eddy-currents) have a meaningful impact on the DTI parameter estimates from tissue.[56] Consequently, this is the topic of a multinational study directed by the diffusion-study group of the ISMRM.
Summary
[edit]For DTI, it is generally possible to use linear algebra, matrix mathematics and vector mathematics to process the analysis of the tensor data.
In some cases, the full set of tensor properties is of interest, but for tractography it is usually necessary to know only the magnitude and orientation of the primary axis or vector. This primary axis—the one with the greatest length—is the largest eigenvalue and its orientation is encoded in its matched eigenvector. Only one axis is needed as it is assumed the largest eigenvalue is aligned with the main axon direction to accomplish tractography.
See also
[edit]Explanatory notes
[edit]- ^ Several full mathematical treatments of general tensors exist, e.g. classical, component free, and so on, but the generality, which covers arrays of all sizes, may obscure rather than help.
References
[edit]- ^ a b Le Bihan, Denis; Breton, E. (1985). "Imagerie de diffusion in-vivo par résonance magnétique nucléaire" [In-vivo diffusion imaging by nuclear magnetic resonance]. Comptes Rendus de l'Académie des Sciences (in French). 301 (15): 1109–1112. INIST 8814916.
- ^ Merboldt KD, Hanicke W, Frahm J (1985). "Self-diffusion NMR imaging using stimulated echoes". Journal of Magnetic Resonance. 64 (3): 479–486. Bibcode:1985JMagR..64..479M. doi:10.1016/0022-2364(85)90111-8.
- ^ Taylor DG, Bushell MC (April 1985). "The spatial mapping of translational diffusion coefficients by the NMR imaging technique". Physics in Medicine and Biology. 30 (4): 345–349. Bibcode:1985PMB....30..345T. doi:10.1088/0031-9155/30/4/009. PMID 4001161. S2CID 250787827.
- ^ Wedeen VJ, Hagmann P, Tseng WY, Reese TG, Weisskoff RM (December 2005). "Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging". Magnetic Resonance in Medicine. 54 (6): 1377–1386. doi:10.1002/mrm.20642. PMID 16247738. S2CID 8586494.
- ^ Wedeen VJ, Wang RP, Schmahmann JD, Benner T, Tseng WY, Dai G, et al. (July 2008). "Diffusion spectrum magnetic resonance imaging (DSI) tractography of crossing fibers". NeuroImage. 41 (4): 1267–1277. doi:10.1016/j.neuroimage.2008.03.036. PMID 18495497. S2CID 2660208.
- ^ Le Bihan D, Breton E, Lallemand D, Grenier P, Cabanis E, Laval-Jeantet M (November 1986). "MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders". Radiology. 161 (2): 401–407. doi:10.1148/radiology.161.2.3763909. PMID 3763909.
- ^ Wang Y, Wang Q, Haldar JP, Yeh FC, Xie M, Sun P, et al. (December 2011). "Quantification of increased cellularity during inflammatory demyelination". Brain. 134 (Pt 12): 3590–3601. doi:10.1093/brain/awr307. PMC 3235568. PMID 22171354.
- ^ Vavasour, Irene M; Sun, Peng; Graf, Carina; Yik, Jackie T; Kolind, Shannon H; Li, David KB; Tam, Roger; Sayao, Ana-Luiza; Schabas, Alice; Devonshire, Virginia; Carruthers, Robert; Traboulsee, Anthony; Moore, GR Wayne; Song, Sheng-Kwei; Laule, Cornelia (March 2022). "Characterization of multiple sclerosis neuroinflammation and neurodegeneration with relaxation and diffusion basis spectrum imaging". Multiple Sclerosis Journal. 28 (3): 418–428. doi:10.1177/13524585211023345. PMC 9665421. PMID 34132126.
- ^ Ye, Zezhong; George, Ajit; Wu, Anthony T.; Niu, Xuan; Lin, Joshua; Adusumilli, Gautam; Naismith, Robert T.; Cross, Anne H.; Sun, Peng; Song, Sheng-Kwei (May 2020). "Deep learning with diffusion basis spectrum imaging for classification of multiple sclerosis lesions". Annals of Clinical and Translational Neurology. 7 (5): 695–706. doi:10.1002/acn3.51037. PMC 7261762. PMID 32304291.
- ^ Ye, Zezhong; Price, Richard L.; Liu, Xiran; Lin, Joshua; Yang, Qingsong; Sun, Peng; Wu, Anthony T.; Wang, Liang; Han, Rowland H.; Song, Chunyu; Yang, Ruimeng; Gary, Sam E.; Mao, Diane D.; Wallendorf, Michael; Campian, Jian L. (2020-10-15). "Diffusion Histology Imaging Combining Diffusion Basis Spectrum Imaging (DBSI) and Machine Learning Improves Detection and Classification of Glioblastoma Pathology". Clinical Cancer Research. 26 (20): 5388–5399. doi:10.1158/1078-0432.ccr-20-0736. PMC 7572819. PMID 32694155.
- ^ Ye, Zezhong; Srinivasa, Komal; Meyer, Ashely; Sun, Peng; Lin, Joshua; Viox, Jeffrey D.; Song, Chunyu; Wu, Anthony T.; Song, Sheng-Kwei; Dahiya, Sonika; Rubin, Joshua B. (2021-02-26). "Diffusion histology imaging differentiates distinct pediatric brain tumor histology". Scientific Reports. 11 (1): 4749. Bibcode:2021NatSR..11.4749Y. doi:10.1038/s41598-021-84252-3. PMC 7910493. PMID 33637807.
- ^ Samara, Amjad; Li, Zhaolong; Rutlin, Jerrel; Raji, Cyrus A.; Sun, Peng; Song, Sheng-Kwei; Hershey, Tamara; Eisenstein, Sarah A. (August 2021). "Nucleus accumbens microstructure mediates the relationship between obesity and eating behavior in adults". Obesity. 29 (8): 1328–1337. doi:10.1002/oby.23201. PMC 8928440. PMID 34227242.
- ^ a b Zhang Y, Wang S, Wu L, Huo Y (Jan 2011). "Multi-channel diffusion tensor image registration via adaptive chaotic PSO". Journal of Computers. 6 (4): 825–829. doi:10.4304/jcp.6.4.825-829.
- ^ King MD, Houseman J, Roussel SA, van Bruggen N, Williams SR, Gadian DG (December 1994). "q-Space imaging of the brain". Magnetic Resonance in Medicine. 32 (6): 707–713. doi:10.1002/mrm.1910320605. PMID 7869892. S2CID 19766099.
- ^ Posse S, Cuenod CA, Le Bihan D (September 1993). "Human brain: proton diffusion MR spectroscopy". Radiology. 188 (3): 719–725. doi:10.1148/radiology.188.3.8351339. PMID 8351339.
- ^ Stejskal EO, Tanner JE (1 January 1965). "Spin Diffusion Measurements: Spin Echoes in the Presence of a Time-Dependent Field Gradient". The Journal of Chemical Physics. 42 (1): 288–292. Bibcode:1965JChPh..42..288S. doi:10.1063/1.1695690.
- ^ Niendorf T, Dijkhuizen RM, Norris DG, van Lookeren Campagne M, Nicolay K (December 1996). "Biexponential diffusion attenuation in various states of brain tissue: implications for diffusion-weighted imaging". Magnetic Resonance in Medicine. 36 (6): 847–857. doi:10.1002/mrm.1910360607. PMID 8946350. S2CID 25910939.
- ^ Kärger, Jörg; Pfeifer, Harry; Heink, Wilfried (1988). Principles and Application of Self-Diffusion Measurements by Nuclear Magnetic Resonance. Advances in Magnetic and Optical Resonance. Vol. 12. pp. 1–89. doi:10.1016/b978-0-12-025512-2.50004-x. ISBN 978-0-12-025512-2.
- ^ Liu C, Bammer R, Moseley ME (2003). "Generalized Diffusion Tensor Imaging (GDTI): A Method for Characterizing and Imaging Diffusion Anisotropy Caused by Non-Gaussian Diffusion". Israel Journal of Chemistry. 43 (1–2): 145–54. doi:10.1560/HB5H-6XBR-1AW1-LNX9.
- ^ Chabert S, Mecca CC, Le Bihan D (2004). Relevance of the information about the diffusion distribution in invo given by kurtosis in q-space imaging. Proceedings, 12th ISMRM Annual Meeting. Kyoto. p. 1238. NAID 10018514722.
- ^ Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K (June 2005). "Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging". Magnetic Resonance in Medicine. 53 (6): 1432–1440. doi:10.1002/mrm.20508. PMID 15906300. S2CID 11865594.
- ^ Torrey HC (1956). "Bloch Equations with Diffusion Terms". Physical Review. 104 (3): 563–565. Bibcode:1956PhRv..104..563T. doi:10.1103/PhysRev.104.563.
- ^ a b Elster AD (2021). "Restricted Diffusion". mriquestions.com/. Retrieved 2018-03-15.
- ^ a b Hammer M. "MRI Physics: Diffusion-Weighted Imaging". XRayPhysics. Retrieved 2017-10-15.
- ^ Le Bihan D (August 2013). "Apparent diffusion coefficient and beyond: what diffusion MR imaging can tell us about tissue structure". Radiology. 268 (2): 318–22. doi:10.1148/radiol.13130420. PMID 23882093.
- ^ An H, Ford AL, Vo K, Powers WJ, Lee JM, Lin W (May 2011). "Signal evolution and infarction risk for apparent diffusion coefficient lesions in acute ischemic stroke are both time- and perfusion-dependent". Stroke. 42 (5): 1276–1281. doi:10.1161/STROKEAHA.110.610501. PMC 3384724. PMID 21454821.
- ^ Bhuta S. "Diffusion weighted MRI in acute stroke". Radiopaedia. Retrieved 2017-10-15.
- ^ Manenti G, Carlani M, Mancino S, Colangelo V, Di Roma M, Squillaci E, Simonetti G (June 2007). "Diffusion tensor magnetic resonance imaging of prostate cancer". Investigative Radiology. 42 (6): 412–419. doi:10.1097/01.rli.0000264059.46444.bf. hdl:2108/34611. PMID 17507813. S2CID 14173858.
- ^ Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A (October 2000). "In vivo fiber tractography using DT-MRI data". Magnetic Resonance in Medicine. 44 (4): 625–632. doi:10.1002/1522-2594(200010)44:4<625::AID-MRM17>3.0.CO;2-O. PMID 11025519.
- ^ Nye, John Frederick (1957). Physical Properties of Crystals: Their Representation by Tensors and Matrices. Clarendon Press. OCLC 576214706.[page needed]
- ^ de Sénarmont HH (1848). "Mémoire sur la conductibilité des substances cristalisées pour la chaleur" [Memoir on the conductivity of crystallized substances for heat]. Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences (in French). 25: 459–461.
- ^ Le Bihan D, Mangin JF, Poupon C, Clark CA, Pappata S, Molko N, Chabriat H (April 2001). "Diffusion tensor imaging: concepts and applications". Journal of Magnetic Resonance Imaging. 13 (4): 534–546. doi:10.1002/jmri.1076. PMID 11276097. S2CID 7269302.
- ^ Richards TL, Heide AC, Tsuruda JS, Alvord EC (1992). Vector analysis of diffusion images in experimental allergic encephalomyelitis (PDF). Proceedings of the Society for Magnetic Resonance in Medicine. Vol. 11. Berlin. p. 412.
- ^ Vaillancourt DE, Spraker MB, Prodoehl J, Abraham I, Corcos DM, Zhou XJ, et al. (April 2009). "High-resolution diffusion tensor imaging in the substantia nigra of de novo Parkinson disease". Neurology. 72 (16): 1378–1384. doi:10.1212/01.wnl.0000340982.01727.6e. PMC 2677508. PMID 19129507.
- ^ Westin CF, Peled S, Gudbjartsson H, Kikinis R, Jolesz FA (1997). Geometrical diffusion measures for MRI from tensor basis analysis. ISMRM '97. Vancouver Canada. p. 1742.
- ^ Westin CF, Maier SE, Mamata H, Nabavi A, Jolesz FA, Kikinis R (June 2002). "Processing and visualization for diffusion tensor MRI". Medical Image Analysis. 6 (2): 93–108. doi:10.1016/s1361-8415(02)00053-1. PMID 12044998.
- ^ Alexander AL, Lee JE, Lazar M, Field AS (July 2007). "Diffusion tensor imaging of the brain". Neurotherapeutics. 4 (3): 316–329. doi:10.1016/j.nurt.2007.05.011. PMC 2041910. PMID 17599699.
- ^ Grand S, Tahon F, Attye A, Lefournier V, Le Bas JF, Krainik A (December 2013). "Perfusion imaging in brain disease". Diagnostic and Interventional Imaging. 94 (12): 1241–1257. doi:10.1016/j.diii.2013.06.009. PMID 23876408.
- ^ Weerakkody Y, Gaillard F, et al. "Ischaemic stroke". Radiopaedia. Retrieved 2017-10-15.
- ^ Chen F, Ni YC (March 2012). "Magnetic resonance diffusion-perfusion mismatch in acute ischemic stroke: An update". World Journal of Radiology. 4 (3): 63–74. doi:10.4329/wjr.v4.i3.63. PMC 3314930. PMID 22468186.
- ^ Koh DM, Collins DJ (June 2007). "Diffusion-weighted MRI in the body: applications and challenges in oncology". AJR. American Journal of Roentgenology. 188 (6): 1622–1635. doi:10.2214/AJR.06.1403. PMID 17515386.
- ^ Takahara, Taro; Kwee, Thomas C. (2010). "Diffusion-Weighted Whole-Body Imaging with Background Body Signal Suppression (DWIBS)". Diffusion-Weighted MR Imaging. Medical Radiology. pp. 227–252. doi:10.1007/978-3-540-78576-7_14. ISBN 978-3-540-78575-0.
- ^ Deen SS, Priest AN, McLean MA, Gill AB, Brodie C, Crawford R, et al. (July 2019). "Diffusion kurtosis MRI as a predictive biomarker of response to neoadjuvant chemotherapy in high grade serous ovarian cancer". Scientific Reports. 9 (1): 10742. Bibcode:2019NatSR...910742D. doi:10.1038/s41598-019-47195-4. PMC 6656714. PMID 31341212.
- ^ a b Wade RG, Tanner SF, Teh I, Ridgway JP, Shelley D, Chaka B, et al. (16 April 2020). "Diffusion Tensor Imaging for Diagnosing Root Avulsions in Traumatic Adult Brachial Plexus Injuries: A Proof-of-Concept Study". Frontiers in Surgery. 7: 19. doi:10.3389/fsurg.2020.00019. PMC 7177010. PMID 32373625.
- ^ Makris N, Worth AJ, Sorensen AG, Papadimitriou GM, Wu O, Reese TG, et al. (December 1997). "Morphometry of in vivo human white matter association pathways with diffusion-weighted magnetic resonance imaging". Annals of Neurology. 42 (6): 951–962. doi:10.1002/ana.410420617. PMID 9403488. S2CID 18718789.
- ^ Soll E (2015). "DTI (Quantitative), a new and advanced MRI procedure for evaluation of Concussions".
- ^ Wade RG, Whittam A, Teh I, Andersson G, Yeh FC, Wiberg M, Bourke G (9 October 2020). "Diffusion tensor imaging of the roots of the brachial plexus: a systematic review and meta-analysis of normative values". Clinical and Translational Imaging. 8 (6): 419–431. doi:10.1007/s40336-020-00393-x. PMC 7708343. PMID 33282795.
- ^ Griffiths, Timothy T.; Flather, Robert; Teh, Irvin; Haroon, Hamied A.; Shelley, David; Plein, Sven; Bourke, Grainne; Wade, Ryckie G. (2021-07-22). "Diffusion tensor imaging in cubital tunnel syndrome". Scientific Reports. 11 (1): 14982. doi:10.1038/s41598-021-94211-7. ISSN 2045-2322. PMC 8298404. PMID 34294771.
- ^ Rojoa, Djamila; Raheman, Firas; Rassam, Joseph; Wade, Ryckie G. (2021-10-22). "Meta-analysis of the normal diffusion tensor imaging values of the median nerve and how they change in carpal tunnel syndrome". Scientific Reports. 11 (1): 20935. Bibcode:2021NatSR..1120935R. doi:10.1038/s41598-021-00353-z. ISSN 2045-2322. PMC 8536657. PMID 34686721.
- ^ a b Tuch DS (December 2004). "Q-ball imaging". Magnetic Resonance in Medicine. 52 (6): 1358–1372. doi:10.1002/mrm.20279. PMID 15562495. S2CID 1368461.
- ^ Tuch DS, Weisskoff RM, Belliveau JW, Wedeen VJ (1999). High angular resolution diffusion imaging of the human brain (PDF). Proceedings of the 7th Annual Meeting of the ISMRM. Philadelphia. NAID 10027851300.
- ^ Tuch DS, Reese TG, Wiegell MR, Makris N, Belliveau JW, Wedeen VJ (October 2002). "High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity". Magnetic Resonance in Medicine. 48 (4): 577–582. doi:10.1002/mrm.10268. PMID 12353272. S2CID 2048187.
- ^ Hext GR (1963). "The estimation of second-order tensors with related tests and designs". Biometrika. 50 (3–4): 353–373. doi:10.1093/biomet/50.3-4.353.
- ^ Basser PJ, Pajevic S (2007). "Spectral decomposition of a 4th-order covariance tensor: applications to diffusion tensor MRI". Signal Processing. 87 (2): 220–236. Bibcode:2007SigPr..87..220B. CiteSeerX 10.1.1.104.9041. doi:10.1016/j.sigpro.2006.02.050. S2CID 6080176.
- ^ Funk P (1919). "Uber eine geometrische Anwendung der Abelschen Integralgleichnung". Math. Ann. 77: 129–135. doi:10.1007/BF01456824. S2CID 121103537.
- ^ Wade, Ryckie G.; Tam, Winnie; Perumal, Antonia; Pepple, Sophanit; Griffiths, Timothy T.; Flather, Robert; Haroon, Hamied A.; Shelley, David; Plein, Sven; Bourke, Grainne; Teh, Irvin (2023-10-13). "Comparison of distortion correction preprocessing pipelines for DTI in the upper limb". Magnetic Resonance in Medicine. 91 (2): 773–783. doi:10.1002/mrm.29881. ISSN 0740-3194. PMID 37831659. S2CID 264099038.


![{\displaystyle {\frac {S(TE)}{S_{0}}}=\exp \left[-\gamma ^{2}G^{2}\delta ^{2}\left(\Delta -{\frac {\delta }{3}}\right)D\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/355575bbfbd0924e1f733841cfe4a022aafba8e0)











![{\displaystyle \mathrm {ADC} (x,y,z)=\ln[S_{2}(x,y,z)/S_{1}(x,y,z)]/(b_{1}-b_{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9abbc60b76bb6bec8785ad650ea4693ee645b4e)



































![{\displaystyle \mathrm {FA} ={\frac {\sqrt {3((\lambda _{1}-\operatorname {E} [\lambda ])^{2}+(\lambda _{2}-\operatorname {E} [\lambda ])^{2}+(\lambda _{3}-\operatorname {E} [\lambda ])^{2})}}{\sqrt {2(\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2})}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6b99560a24b2b57e604ec988e52d9c379b10219)
![{\textstyle \operatorname {E} [\lambda ]=(\lambda _{1}+\lambda _{2}+\lambda _{3})/3\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b96ae6c5167cd8433f74dfc3c2e14f0745e0e5f)








![{\displaystyle \mathrm {RA} ={\frac {\sqrt {(\lambda _{1}-\operatorname {E} [\lambda ])^{2}+(\lambda _{2}-\operatorname {E} [\lambda ])^{2}+(\lambda _{3}-\operatorname {E} [\lambda ])^{2}}}{{\sqrt {3}}\operatorname {E} [\lambda ]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9510ba237aa82760cef9a3e17be0f1fcd440f8bb)
![{\displaystyle \mathrm {VR} ={\frac {\lambda _{1}\lambda _{2}\lambda _{3}}{\operatorname {E} [\lambda ]^{3}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd11dafd0f15f1c16165bc6eec8e95583af05af8)


