اثر پروانه‌ای

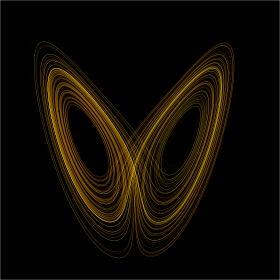
اثر پروانه‌ای نام پدیده‌ای است که به دلیل حساسیت سیستم‌های آشوب‌ناک به شرایط اولیه ایجاد می‌شود. این پدیده به این اشاره می‌کند که تغییری کوچک در یک سیستم آشوب‌ناک چون جو سیارهٔ زمین (مانند بال‌زدن پروانه) می‌تواند باعث تغییرات شدید (وقوع طوفان در کشوری دیگر) در آینده شود. اثر پروانه‌ای به این معناست که تغییر جزئی در شرایط اولیه می‌تواند به نتایج وسیع و پیش‌بینی نشده در ستاده‌های سیستم منجر گردد و این سنگ بنای تئوری آشوب است. در نظریه آشوب یا بی‌نظمی اعتقاد بر آن است که در تمامی پدیده‌ها، نقاطی وجود دارند که تغییری اندک در آن‌ها باعث تغییرات عظیم خواهد شد و در این رابطه سیستم‌های اقتصادی، سیاسی، اجتماعی و سازمانی، همچون سیستم‌های جوی از اثر پروانه‌ای برخوردارند و تحلیلگران باید با آگاهی از این نکته مهم به تحلیل و تنظیم مسائل مربوط بپردازند.^[۱]

ایدهٔ این‌که پروانه‌ای می‌تواند باعث تغییری آشوبی شود نخستین بار در ۱۹۵۲ در داستان کوتاهی به نام آوای تندر اثر ری بردبری مطرح شد. عبارت «اثر پروانه‌ای» هم در ۱۹۶۱ در پی مقاله‌ای از ادوارد لورنتس به وجود آمد. وی در صد و سی و نهمین اجلاس ای‌ای‌ای‌اس در سال ۱۹۷۲ مقاله‌ای با این عنوان ارائه داد که «آیا بال‌زدن پروانه‌ای در برزیل می‌تواند باعث ایجاد تندباد در تگزاس شود؟»

لورنتس در پژوهش بر روی مدل ریاضی بسیار ساده‌ای از آب و هوای جو زمین، به معادلهٔ دیفرانسیل غیرقابل حل رسید. وی برای حل این معادله از روش‌های عددی به کمک رایانه بهره جست. او برای این‌که بتواند این کار را در روزهای متوالی انجام دهد، نتیجه آخرین خروجی یک روز را به عنوان شرایط اولیه روز بعد وارد می‌کرد. لورنتس در نهایت مشاهده کرد که نتیجه شبیه‌سازی‌های مختلف با شرایط اولیه یکسان با هم کاملاً متفاوت است. بررسی خروجی چاپ شده رایانه نشان داده که رویال مک‌بی (Royal McBee)، رایانه‌ای که لورنتس از آن استفاده می‌کرد، خروجی را تا ۳ رقم اعشار گرد می‌کند. از آنجایی که محاسبات داخل این رایانه با ۶ رقم اعشار صورت می‌گرفت، از بین رفتن سه رقم آخر باعث چنین تأثیری شده بود. مقدار تغییرات در عمل گردکردن نزدیک به اثر بال‌زدن یک پروانه‌است. این واقعیت غیرممکن بودن پیش‌بینی آب و هوا در دراز مدت را نشان می‌دهد.

مشاهدات لورنتس باعث پررنگ شدن مبحث نظریه آشوب شد. عبارت عامیانه «اثر پروانه‌ای» در زبان تخصصی نظریه آشوب، «وابستگی حساس به شرایط اولیه» ترجمه می‌شود.

به غیر از آب و هوا، در سیستم‌های پویای دیگر نیز حساسیت به شرایط اولیه به چشم می‌خورد. یک مثال ساده، توپی است که در قله کوهی قرار گرفته. این توپ با ضربه بسیار کمی، بسته به اینکه ضربه از چه جهتی زده شده باشد، می‌تواند به هرکدام از دره‌های اطراف سقوط کند.

اغلب سیستم‌ها در دنیای واقعی طی تکرار یک عملیات مشخص کار می‌کنند. در مثال آب و هوای لورنتس فرایند گرم شدن سطح زمین از طرف خورشید و سرد شدن جو از طریق تابش به فضای بیرون، فرایندی است که مدام تکرار می‌شود. می‌توان نشان داد که در چنین سیستمی بازه‌ای از مقادیر اولیه باعث ایجاد رفتار آشوبناک می‌شود. مثال ساده زیر را در نظر بگیرید:

برای اینکه نتیجه عملکرد سیستم فوق را بتوانیم بهتر درک کنیم از نموداری به این شرح استفاده می‌کنیم. ابتدا تابع ${\displaystyle y=x^{2}+c}$ را رسم کرده و خط ${\displaystyle y=x}$ را نیز روی آن می‌کشیم. روی نمودار، مقداری اولیه‌ای برای ${\displaystyle x_{0}}$ در نظر می‌گیریم. مقدار ${\displaystyle x_{1}}$ با رسم یک خط عمودی از این عدد تا نمودار ${\displaystyle y=x^{2}+c}$ بدست می‌آید. برای بدست آوردن نقطه بعدی باید مقدار قبلی y را به جای مقدار فعلی x بگذاریم. این کار با رسم یک خط افقی از نقطه برخورد قبلی تا نمودار ${\displaystyle y=x}$ انجام می‌شود. شکل‌های زیر با در نظر گرفتن ${\displaystyle x_{0}=0}$ و به ترتیب، از راست به چپ، ${\displaystyle c={\frac {1}{4}},-{\frac {3}{4}},-1.3,-1.4015,-1.8}$ رسم شده‌اند:

مشاهده می‌شود که با ایجاد تغییرات جزئی در پارامتر، رفتار سیستم کاملاً تغییر می‌کند. به چنین رفتاری «وابستگی حساس به شرایط اولیه» یا «اثر پروانه‌ای» می‌گویند.

اگر مجموعه مقادیری که x در طول عملکرد سیستم به خود می‌گیرد را نسبت به c رسم کنیم، شکل بدست آمده یک فراکتال (برخال) خواهد بود:

یک سیستم پویا بانقشه تکامل ${\displaystyle f^{t}}$ وابستگی حساس به شرایط اولیه دارد، اگر نقاط نزدیک به هم با افزایش t از هم جدا شوند. اگر M فضای حالت نقشه ${\displaystyle f^{t}}$ باشد، می‌گوییم ${\displaystyle f^{t}}$ به شرایط اولیه وابستگی حساس نشان می‌دهد وقتی که حداقل یک δ>۰ وجود داشته باشد به‌طوری که به ازای هر نقطه x∈M و هر همسایگی از N که x را دربرداشته باشد، نقطه‌ای مانند y در همسایگی N موجود بوده و در زمانی مانند τ رابطه ${\displaystyle d(f^{\tau }(x),f^{\tau }(y))>\mathrm {e} ^{a\tau }\,d(x,y).}$ برقرار باشد.

در این تعریف نیازی نیست که همه نقاط موجود در یک همسایگی، از نقطه مبنای x جدا باشند.

مفهوم اثر پروانه‌ای از جهاتی برای نوشتن داستان‌هایی دربارهٔ سفر زمان جذاب است، فیلم اثر پروانه‌ای ساخت نیولاین سینما، کاملاً از این مفهوم در سفر زمان سود برده‌است.

برداشت‌های تخیلی فراوانی از کاربرد اثر پروانه‌ای در سفر زمان انجام گرفته‌است. بسیاری بر این باورند که فیلم «اثر پروانه‌ای» ساخته شده در سال ۲۰۰۴ میلادی، نمونهٔ خوبی است که نشان می‌دهد در صورت ممکن شدن سفر در زمان، دستکاری مسائل کوچک و جزئی در گذشته، می‌تواند آینده را به طرز ناگواری دگرگون کند. یک تفسیر بهتر و منتقدپسندانه تر از این مفهوم، در فیلم «فرکانس» محصول سال ۲۰۰۰ میلادی ارائه شده‌است. در این فیلم، پدر و پسر در راستای زمان، از طریق امواج رادیویی با یکدیگر رابطه برقرار می‌کنند و سعی می‌کنند گذشته را برای به دست آوردن نتایج مطلوب، تغییر دهند. همچنین در یکی از اپیزودهای سریال ۱۳ دلیل برای اینکه به توضیح دربارهٔ اثر پروانه ای می‌پردازد و در آخر ۱۳ دلیل را همانند اثر پروانه ای می‌داند که هسته اصلی این سریال است.

تراویس اسکات، در آلبوم Astroworld آهنگی به نام اثر پروانه‌ای خوانده‌است.

همچنین گروه موسیقی کره ای به نام اکسو (EXO) در آلبوم Obsession آهنگی به نام اثر پروانه ای خوانده‌است.

• فیلم اثر پروانه‌ای
• آوای تندر
• واکنش زنجیره‌ای
• نظریه دومینو
• ویژگی دومینو
• فیلم فرکانس

• Butterfly Effect (بازنویسی مفاهیم ریاضی) (انگلیسی)
• From butterfly wings to single e-mail (دانشگاه کارنل) (انگلیسی)
• New England Complex Systems InstituteConcepts: Butterfly Effect (انگلیسی)
• The Chaos Hypertextbook. مقدمه‌ای بر نظریه آشوب (چاوس) و برخال‌ها. (انگلیسی)
• The Butterfly Effect. فیلم اثر پروانه‌ای ساخت نیولاین سینما IMDB
• Butterfly Effect نوشته اریک دبلیو ویستین در وبسایت دنیای ریاضی (انگلیسی)

• Robert L. Devaney (۲۰۰۳)، Introduction to Chaotic Dynamical Systems، Westview Press، شابک ۰-۸۱۳۳-۴۰۸۵-۳
• Robert C. Hilborn (۲۰۰۴)، «Sea gulls, butterflies, and grasshoppers: A brief history of the butterfly effect in nonlinear dynamics»، American Journal of Physics، ش. ۷۲، ص. ۴۲۵–۴۲۷
• نظام‌الدین فقیه، [[آشوب]] و فراکتال در سیستم‌های پویا ۹۶۴-۹۴۳۶۷-۱-۵:شابک^[۲]
• نظام‌الدین فقیه، رموز تحول و توسعه در سیستم‌های انسانی (نگرشی نوین) ۹۶۴-۳۵۸-۲۶۵-۵:شابک^[۳][۴]