یک مثال از طرح کاپلان–مه‌یر برای دو وضعیت مرتبط با بقای بیماران
برآوردگر کاپلان–مه‌یر (به انگلیسی: Kaplan–Meier estimator)،[۱][۲] همچنین معروف به برآوردگر حد محصول، یک برآوردگر برای تخمین تابع بقا از اطلاعات مدت حیات است. در تحقیق پزشکی، اغلب برای اندازه‌گیری کسر بیماران زنده تا مدت زمانی مشخصی بعد از درمان استفاده می‌گردد. در اقتصاد، می‌توان از آن برای استفاده جهت اندازه‌گیری مدت زمان افرادی که بعد از از دست دادن شغل بیکار می‌مانند به کار گرفت. در مهندسی، برای اندازه‌گیری زمان باقی‌مانده تا خرابی قطعات یک ماشین مورد استفاده قرار می‌گیرد. در بوم شناسی، برای برآورد مدت زمان باقی ماندن میوه‌های گوشتی بر روی گیاهان قبل از اینکه توسط میوه خواران از بین بروند، به کار می‌رود. برآوردگر بعد از ادوارد ال. کاپلان و پل مه‌یر نامگذاری شد. هر دوی شان مقالهٔ مشابهی به مجله مؤسسه آماری آمریکا ارسال نمودند، اما ویرایش‌گر تصمیم گرفت که کار آن‌ها را با ترکیب شان تبدیل به یک مقاله کند، که حدود ۳۴۰۰۰ دفعه از زمان انتشارش مورد ارجاع قرار گرفته‌است.[۳]
طرحی از برآورد تابع بقای کاپلان–مه‌یر یک سری از مراحل افقی مقدار در حال کاهش است که در آن، وقتی یک نمونه به قدر کافی بزرگ بررسی می‌شود، تابع بقای صحیح برای آن جمعیت به دست می‌آید. مقدار تابع بقا بین مشاهدات نمونه برداری شدهٔ موفق متمایز از هم ("تیک ها") ثابت فرض می‌شود.
مزیت مهم منحنی کاپلان–مه‌یر این است که این روش بعضی انواع داده سانسورشده را مورد حساب قرار می‌دهد، به‌طور خاص سانسور درست که اگر یک بیمار از مطالعه‌ای به عنوان مثال قبل از مشاهدهٔ نتیجه نهایی، از نمونه خارج شود، رخ می‌دهد. در طرح، نشان‌های تیک کوچک به‌طور عمودی نشانگر تلفات هستند، جایی که زمان بقای یک بیمار درست سانسور شده باشد. وقتی هیچ کاهش یا سانسوری رخ ندهد، منحنی کاپلان–مه‌یر متمم تابع توزیع نمونه‌ای می‌شود.
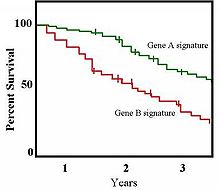
در آمار پزشکی، یک کاربرد عادی می‌تواند بیمارهای گروه بندی شده را در دسته‌هایی قرار دهد، برای مثال، آن‌هایی که نمایهٔ ژن A را دارند و آن‌هایی که نمایهٔ ژن B را دارند. در نمودار، بیمارها با ژن B سریع تر از آن‌هایی که ژن A دارند، می‌میرند. بعد از دو سال، حدود ۸۰ درصد بیمارهای با ژن A زنده می‌مانند، اما کمتر از نصف بیمارهای با ژن B نجات می‌یابند.
