Полуправильный многогранник

Полуправильные многогранники — в общем случае это различные выпуклые многогранники, которые, не являясь правильными, имеют некоторые их признаки, например: все грани равны, или все грани являются правильными многоугольниками, или имеются определённые пространственные симметрии. Определение может варьироваться и включать различные типы многогранников, но в первую очередь сюда относятся архимедовы тела.

Полуправильными в этом случае называются многоранники, у которых отсутствует только одно из первых двух из следующих свойств правильных тел:

• Все грани являются правильными многоугольниками;
• Все грани одинаковы;
• Тело относится к одному из трёх существующих типов пространственной симметрии (тетраэдральной, октаэдральной или икосаэдрической).

Архимедовы — тела, у которых отсутствует второе свойство, у каталановых отсутствует первое, третье свойство сохраняется для обоих видов тел. Тела, не обладающие третьим свойством, называются телами Джонсона (некоторые из которых не обладают и вторым свойством) и не относятся к полуправильным.

Помимо архимедовых и каталановых тел к полуправильным многогранникам иногда относят и бесконечные последовательности призм и антипризм, у которых также отсутствует только второе свойство. Призмы и антипризмы, однако, относятся к диэдральной группе симметрии, для которой не существует правильных многогранников.

Архимедовы тела — выпуклые многогранники, обладающие двумя свойствами:

• Все грани являются правильными многоугольниками двух или более типов (если все грани — правильные многоугольники одного типа, это — правильный многогранник, или платоново тело);
• для любой пары вершин существует симметрия многогранника (то есть движение, переводящее многогранник в себя), переводящая одну вершину в другую. В частности,
  • все многогранные углы при вершинах конгруэнтны.

Первое построение полуправильных многогранников приписывается Архимеду, хотя соответствующие работы утеряны.

Все архимедовы тела являются правильногранными многогранниками.

Тела, двойственные архимедовым, так называемые каталановы тела, имеют конгруэнтные грани (переводимые друг в друга сдвигом, вращением или отражением), равные двугранные углы и правильные многогранные углы. Каталановы тела тоже иногда называют полуправильными многогранниками. В этом случае полуправильными многогранниками считается совокупность архимедовых и каталановых тел. Архимедовы тела являются полуправильными многогранниками в том смысле, что их грани — правильные многоугольники, но они не одинаковы, а каталановы — в том смысле, что их грани одинаковы, но не являются правильными многоугольниками; при этом для тех и других сохраняется условие одного из типов пространственной симметрии: тетраэдрического, октаэдрического или икосаэдрического.

Существует 13 архимедовых тел, два из которых (курносый куб и плосконосый додекаэдр) не являются зеркально-симметричными и имеют левую и правую формы. Если учитывать левую и правую форму как отдельные тела, тогда получится 15 архимедовых тел. Соответственно, существует 13 (15) каталановых тел.

Многогранник — архимедово тело	Грани	Вершины	Рёбра	Конфигурация вершины	Двойственный — каталаново тело	Группа симметрии
Кубооктаэдр	8 треугольников 6 квадратов	12	24	3,4,3,4	Ромбододекаэдр	Oh
Икосододекаэдр	20 треугольников 12 пятиугольников	30	60	3,5,3,5	Ромботриаконтаэдр	Ih
Усечённый тетраэдр	4 треугольника 4 шестиугольника	12	18	3,6,6	Триакистетраэдр	Td
Усечённый октаэдр	6 квадратов 8 шестиугольников	24	36	4,6,6	Тетракисгексаэдр (преломлённый куб)	Oh
Усечённый икосаэдр	12 пятиугольников 20 шестиугольников	60	90	5,6,6	Пентакисдодекаэдр	Ih
Усечённый куб	8 треугольников 6 восьмиугольников	24	36	3,8,8	Триакисоктаэдр	Oh
Усечённый додекаэдр	20 треугольников 12 десятиугольников	60	90	3,10,10	Триакисикосаэдр	Ih
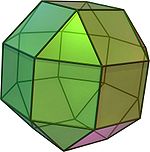Ромбокубоктаэдр	8 треугольников 18 квадратов (6 — в кубическом положении, 12 — в ромбическом)	24	48	3,4,4,4	Дельтоидальный икоситетраэдр	Oh
Ромбоикосододекаэдр	20 треугольников 30 квадратов 12 пятиугольников	60	120	3,4,5,4	Дельтоидальный гексеконтаэдр	Ih
Ромбоусечённый кубооктаэдр	12 квадратов 8 шестиугольников 6 восьмиугольников	48	72	4,6,8	Гекзакисоктаэдр	Oh
Ромбоусечённый икосододекаэдр	30 квадратов 20 шестиугольников 12 десятиугольников	120	180	4,6,10	Гекзакисикосаэдр	Ih
Курносый куб	32 треугольника 6 квадратов	24	60	3,3,3,3,4	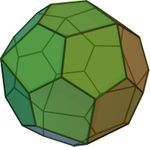Пентагональный икоситетраэдр	O
Курносый додекаэдр	80 треугольников 12 пятиугольников	60	150	3,3,3,3,5	Пентагональный гексеконтаэдр	I

Каталановы тела — наряду с платоновыми телами, равногранными бипирамидами и трапецоэдрами — используются в качестве игральных костей в некоторых настольных играх (см. фотографии). Архимедовы тела, у которых грани не равноправны и потому имеют разные шансы выпадения, для этой цели мало пригодны.

• Правильный многогранник
• Звёздчатый многогранник
• Призма
• Антипризма
• Многогранник Джонсона

• Ашкинузе В. Г. О числе полуправильных многогранников // Математическое просвещение. Вторая серия. — 1957. — Вып. 1. — С. 107-118.
• Залгаллер В. А. Выпуклые многогранники с правильными гранями// Записки научных семинаров ЛОМИ. Том 2 -- 1966.