Duoprism

Set of uniform p-q duoprisms
Type	Prismatic uniform 4-polytopes
Schläfli symbol	{p}×{q}
Coxeter-Dynkin diagram
Cells	p q-gonal prisms, q p-gonal prisms
Faces	pq squares, p q-gons, q p-gons
Edges	2pq
Vertices	pq
Vertex figure	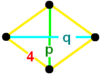disphenoid
Symmetry	[p,2,q], order 4pq
Dual	p-q duopyramid
Properties	convex, vertex-uniform
Set of uniform p-p duoprisms
Type	Prismatic uniform 4-polytope
Schläfli symbol	{p}×{p}
Coxeter-Dynkin diagram
Cells	2p p-gonal prisms
Faces	p2 squares, 2p p-gons
Edges	2p2
Vertices	p2
Symmetry	[p,2,p] = [2p,2+,2p], order 8p2
Dual	p-p duopyramid
Properties	convex, vertex-uniform, Facet-transitive

In geometry of 4 dimensions or higher, a double prism^[1] or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an n-polytope and an m-polytope is an (n+m)-polytope, where n and m are dimensions of 2 (polygon) or higher.

The lowest-dimensional duoprisms exist in 4-dimensional space as 4-polytopes being the Cartesian product of two polygons in 2-dimensional Euclidean space. More precisely, it is the set of points:

${\displaystyle P_{1}\times P_{2}=\{(x,y,z,w)|(x,y)\in P_{1},(z,w)\in P_{2}\}}$

where P₁ and P₂ are the sets of the points contained in the respective polygons. Such a duoprism is convex if both bases are convex, and is bounded by prismatic cells.

Four-dimensional duoprisms are considered to be prismatic 4-polytopes. A duoprism constructed from two regular polygons of the same edge length is a uniform duoprism.

A duoprism made of n-polygons and m-polygons is named by prefixing 'duoprism' with the names of the base polygons, for example: a triangular-pentagonal duoprism is the Cartesian product of a triangle and a pentagon.

An alternative, more concise way of specifying a particular duoprism is by prefixing with numbers denoting the base polygons, for example: 3,5-duoprism for the triangular-pentagonal duoprism.

Other alternative names:

• q-gonal-p-gonal prism
• q-gonal-p-gonal double prism
• q-gonal-p-gonal hyperprism

The term duoprism is coined by George Olshevsky, shortened from double prism. John Horton Conway proposed a similar name proprism for product prism, a Cartesian product of two or more polytopes of dimension at least two. The duoprisms are proprisms formed from exactly two polytopes.

Schlegel diagram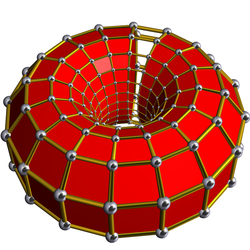 Projection from the center of one 16-gonal prism, and all but one of the opposite 16-gonal prisms are shown.

net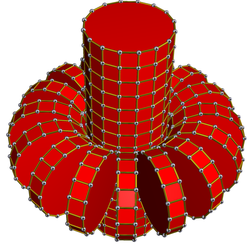 The two sets of 16-gonal prisms are shown. The top and bottom faces of the vertical cylinder are connected when folded together in 4D.

A 4-dimensional uniform duoprism is created by the product of a regular n-sided polygon and a regular m-sided polygon with the same edge length. It is bounded by n m-gonal prisms and m n-gonal prisms. For example, the Cartesian product of a triangle and a hexagon is a duoprism bounded by 6 triangular prisms and 3 hexagonal prisms.

• When m and n are identical, the resulting duoprism is bounded by 2n identical n-gonal prisms. For example, the Cartesian product of two triangles is a duoprism bounded by 6 triangular prisms.
• When m and n are identically 4, the resulting duoprism is bounded by 8 square prisms (cubes), and is identical to the tesseract.

The m-gonal prisms are attached to each other via their m-gonal faces, and form a closed loop. Similarly, the n-gonal prisms are attached to each other via their n-gonal faces, and form a second loop perpendicular to the first. These two loops are attached to each other via their square faces, and are mutually perpendicular.

As m and n approach infinity, the corresponding duoprisms approach the duocylinder. As such, duoprisms are useful as non-quadric approximations of the duocylinder.

3-3
3-4	4-4
3-5	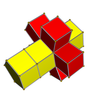4-5	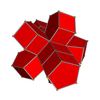5-5
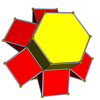3-6	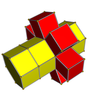4-6	5-6	6-6
3-7	4-7	5-7	6-7	7-7
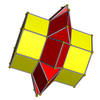3-8	4-8	5-8	6-8	7-8	8-8
3-9	4-9	5-9	6-9	7-9	8-9	9-9
3-10	4-10	5-10	6-10	7-10	8-10	9-10	10-10

A cell-centered perspective projection makes a duoprism look like a torus, with two sets of orthogonal cells, p-gonal and q-gonal prisms.

Schlegel diagrams

6-prism	6-6 duoprism
A hexagonal prism, projected into the plane by perspective, centered on a hexagonal face, looks like a double hexagon connected by (distorted) squares. Similarly a 6-6 duoprism projected into 3D approximates a torus, hexagonal both in plan and in section.

The p-q duoprisms are identical to the q-p duoprisms, but look different in these projections because they are projected in the center of different cells.

Schlegel diagrams

3-3	3-4	3-5	3-6	3-7	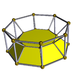3-8
4-3	4-4	4-5	4-6	4-7	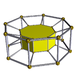4-8
5-3	5-4	5-5	5-6	5-7	5-8
6-3	6-4	6-5	6-6	6-7	6-8
7-3	7-4	7-5	7-6	7-7	7-8
8-3	8-4	8-5	8-6	8-7	8-8

Vertex-centered orthogonal projections of p-p duoprisms project into [2n] symmetry for odd degrees, and [n] for even degrees. There are n vertices projected into the center. For 4,4, it represents the A₃ Coxeter plane of the tesseract. The 5,5 projection is identical to the 3D rhombic triacontahedron.

Orthogonal projection wireframes of p-p duoprisms

Odd
3-3			5-5			7-7			9-9
[3]		[6]	[5]		[10]	[7]		[14]	[9]		[18]
Even
4-4 (tesseract)			6-6			8-8			10-10
[4]		[8]	[6]		[12]	[8]		[16]	[10]		[20]

The regular skew polyhedron, {4,4|n}, exists in 4-space as the n² square faces of a n-n duoprism, using all 2n² edges and n² vertices. The 2n n-gonal faces can be seen as removed. (skew polyhedra can be seen in the same way by a n-m duoprism, but these are not regular.)

Like the antiprisms as alternated prisms, there is a set of 4-dimensional duoantiprisms: 4-polytopes that can be created by an alternation operation applied to a duoprism. The alternated vertices create nonregular tetrahedral cells, except for the special case, the 4-4 duoprism (tesseract) which creates the uniform (and regular) 16-cell. The 16-cell is the only convex uniform duoantiprism.

The duoprisms , t_0,1,2,3{p,2,q}, can be alternated into , ht_0,1,2,3{p,2,q}, the "duoantiprisms", which cannot be made uniform in general. The only convex uniform solution is the trivial case of p=q=2, which is a lower symmetry construction of the tesseract , t_0,1,2,3{2,2,2}, with its alternation as the 16-cell, , s{2}s{2}.

The only nonconvex uniform solution is p=5, q=5/3, ht_0,1,2,3{5,2,5/3}, , constructed from 10 pentagonal antiprisms, 10 pentagrammic crossed-antiprisms, and 50 tetrahedra, known as the great duoantiprism (gudap).^[2][3]

Also related are the ditetragoltriates or octagoltriates, formed by taking the octagon (considered to be a ditetragon or a truncated square) to a p-gon. The octagon of a p-gon can be clearly defined if one assumes that the octagon is the convex hull of two perpendicular rectangles; then the p-gonal ditetragoltriate is the convex hull of two p-p duoprisms (where the p-gons are similar but not congruent, having different sizes) in perpendicular orientations. The resulting polychoron is isogonal and has 2p p-gonal prisms and p² rectangular trapezoprisms (a cube with D_2d symmetry) but cannot be made uniform. The vertex figure is a triangular bipyramid.

Like the duoantiprisms as alternated duoprisms, there is a set of p-gonal double antiprismoids created by alternating the 2p-gonal ditetragoltriates, creating p-gonal antiprisms and tetrahedra while reinterpreting the non-corealmic triangular bipyramidal spaces as two tetrahedra. The resulting figure is generally not uniform except for two cases: the grand antiprism and its conjugate, the pentagrammic double antiprismoid (with p = 5 and 5/3 respectively), represented as the alternation of a decagonal or decagrammic ditetragoltriate. The vertex figure is a variant of the sphenocorona.

The 3-3 duoprism, -1₂₂, is first in a dimensional series of uniform polytopes, expressed by Coxeter as k₂₂ series. The 3-3 duoprism is the vertex figure for the second, the birectified 5-simplex. The fourth figure is a Euclidean honeycomb, 2₂₂, and the final is a paracompact hyperbolic honeycomb, 3₂₂, with Coxeter group [3^2,2,3], ${\displaystyle {\bar {T}}_{7}}$. Each progressive uniform polytope is constructed from the previous as its vertex figure.

k₂₂ figures in n dimensions

Space	Finite			Euclidean	Hyperbolic
n	4	5	6	7	8
Coxeter group	A2A2	E6	${\displaystyle {\tilde {E}}_{6}}$=E6+	${\displaystyle {\bar {T}}_{7}}$=E6++
Coxeter diagram
Symmetry	[[32,2,-1]]	[[32,2,0]]	[[32,2,1]]	[[32,2,2]]	[[32,2,3]]
Order	72	1440	103,680	∞
Graph				∞	∞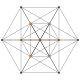
Name	−122	022	122	222	322

• Polytope and 4-polytope
• Convex regular 4-polytope
• Duocylinder
• Tesseract

• Regular Polytopes, H. S. M. Coxeter, Dover Publications, Inc., 1973, New York, p. 124.
• Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues)
  • Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33-62, 1937.
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
• N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966