Spatial reference system

Geodesy
Fundamentals Geodesy Geodynamics Geomatics History
Concepts Geographical distance Geoid Figure of the Earth (radius and circumference) Geodetic coordinates Geodetic datum Geodesic Horizontal position representation Latitude / Longitude Map projection Reference ellipsoid Satellite geodesy Spatial reference system Spatial relations Vertical positions
Technologies Global Nav. Sat. Systems (GNSSs) Global Pos. System (GPS) GLONASS (Russia) BeiDou (BDS) (China) Galileo (Europe) NAVIC (India) Quasi-Zenith Sat. Sys. (QZSS) (Japan) Discrete Global Grid and Geocoding
Standards (history) NGVD 29 Sea Level Datum 1929 OSGB36 Ordnance Survey Great Britain 1936 SK-42 Systema Koordinat 1942 goda ED50 European Datum 1950 SAD69 South American Datum 1969 GRS 80 Geodetic Reference System 1980 ISO 6709 Geographic point coord. 1983 NAD 83 North American Datum 1983 WGS 84 World Geodetic System 1984 NAVD 88 N. American Vertical Datum 1988 ETRS89 European Terrestrial Ref. Sys. 1989 GCJ-02 Chinese obfuscated datum 2002 Geo URI Internet link to a point 2010 International Terrestrial Reference System Spatial Reference System Identifier (SRID) Universal Transverse Mercator (UTM)
v t e

A spatial reference system (SRS) or coordinate reference system (CRS) is a framework used to precisely measure locations on the surface of Earth as coordinates. It is thus the application of the abstract mathematics of coordinate systems and analytic geometry to geographic space. A particular SRS specification (for example, "Universal Transverse Mercator WGS 84 Zone 16N") comprises a choice of Earth ellipsoid, horizontal datum, map projection (except in the geographic coordinate system), origin point, and unit of measure. Thousands of coordinate systems have been specified for use around the world or in specific regions and for various purposes, necessitating transformations between different SRS.

Although they date to the Hellenic Period, spatial reference systems are now a crucial basis for the sciences and technologies of Geoinformatics, including cartography, geographic information systems, surveying, remote sensing, and civil engineering. This has led to their standardization in international specifications such as the EPSG codes^[1] and ISO 19111:2019 Geographic information—Spatial referencing by coordinates, prepared by ISO/TC 211, also published by the Open Geospatial Consortium as Abstract Specification, Topic 2: Spatial referencing by coordinate.^[2]

The thousands of spatial reference systems used today are based on a few general strategies, which have been defined in the EPSG, ISO, and OGC standards:^[1][2]

Geographic coordinate system (or geodetic)

A spherical coordinate system measuring locations directly on the Earth (modeled as a sphere or ellipsoid) using latitude (degrees north or south of the equator) and longitude (degrees west or east of a prime meridian).

Geocentric coordinate system (or Earth-centered Earth-fixed)

A three-dimensional cartesian coordinate system that models the Earth as a three-dimensional object, measuring locations from a center point, usually the center of mass of the Earth, along x, y, and z axes aligned with the equator and the prime meridian. This system is commonly used to track the orbits of satellites, because they are based on the center of mass. Thus, this is the internal coordinate system used by Satellite navigation systems such as GPS to compute locations using multilateration.

Projected coordinate system (or planar, grid)

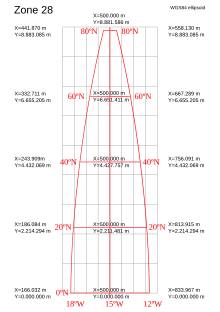
A standardized cartesian coordinate system that models the Earth (or more commonly, a large region thereof) as a plane, measuring locations from an arbitrary origin point along x and y axes more or less aligned with the cardinal directions. Each of these systems is based on a particular Map projection to create a planar surface from the curved Earth surface. These are generally defined and used strategically to minimize the distortions inherent to projections. Common examples include the Universal transverse mercator (UTM) and national systems such as the British National Grid, and State Plane Coordinate System (SPCS).

Engineering coordinate system (or local, custom)

A cartesian coordinate system (2-D or 3-D) that is created bespoke for a small area, often a single engineering project, over which the curvature of the Earth can be safely approximated as flat without significant distortion. Locations are typically measured directly from an arbitrary origin point using surveying techniques. These may or may not be aligned with a standard projected coordinate system. Local tangent plane coordinates are a type of local coordinate system used in aviation and marine vehicles.

Vertical reference frame

a standard reference system for measuring elevation using vertical datums, based on levelling, a geoid model, or a chart datum (considering tides).

These standards acknowledge that standard reference systems also exist for time (e.g. ISO 8601). These may be combined with a spatial reference system to form a compound coordinate system for representing three-dimensional and/or spatio-temporal locations. There are also internal systems for measuring location within the context of an object, such as the rows and columns of pixels in a raster image, Linear referencing measurements along linear features (e.g., highway mileposts), and systems for specifying location within moving objects such as ships. The latter two are often classified as subcategories of engineering coordinate systems.

The goal of any spatial reference system is to create a common reference frame in which locations can be measured precisely and consistently as coordinates, which can then be shared unambiguously, so that any recipient can identify the same location that was originally intended by the originator.^[3] To accomplish this, any coordinate reference system definition needs to be composed of several specifications:

• A coordinate system, an abstract framework for measuring locations. Like any mathematical coordinate system, its definition consists of a measurable space (whether a plane, a three-dimension void, or the surface of an object such as the Earth), an origin point, a set of axis vectors emanating from the origin, and a unit of measure.
• A geodetic datum (horizontal, vertical, or three-dimensional) which binds the abstract coordinate system to the real space of the Earth. A horizontal datum can be defined as a precise reference framework for measuring geographic coordinates (latitude and longitude). Examples include the World Geodetic System and the 1927 and 1983 North American Datum. A datum generally consists of an estimate of the shape of the Earth (usually an ellipsoid), and one or more anchor points or control points, established locations (often marked by physical monuments) for which the measurement is documented.
• A definition for a projected CRS must also include a choice of map projection to convert the spherical coordinates specified by the datum into cartesian coordinates on a planar surface.

Thus, a CRS definition will typically consist of a "stack" of dependent specifications, as exemplified in the following table:

Examples of systems around the world are:

• Chinese Global Navigation Grid Code, China
• Israeli Cassini Soldner, Israel
• Israeli Transverse Mercator, Israel
• Jordan Transverse Mercator, Jordan

• British national grid reference system, Britain
• Lambert-93 (fr), the official projection in Metropolitan France
• Hellenic Geodetic Reference System 1987, Greece
• Irish grid reference system, Ireland
• Irish Transverse Mercator, Ireland
• SWEREF 99 (sv), Sweden

• United States National Grid, US

• Universal Transverse Mercator coordinate system
• Lambert conformal conic projection
• International mapcode system
• Military Grid Reference System

A Spatial Reference System Identifier (SRID) is a unique value used to unambiguously identify projected, unprojected, and local spatial coordinate system definitions. These coordinate systems form the heart of all GIS applications.

Virtually all major spatial vendors have created their own SRID implementation or refer to those of an authority, such as the EPSG Geodetic Parameter Dataset.

SRIDs are the primary key for the Open Geospatial Consortium (OGC) spatial_ref_sys metadata table for the Simple Features for SQL Specification, Versions 1.1 and 1.2, which is defined as follows:

CREATE TABLE SPATIAL_REF_SYS (     SRID      INTEGER   NOT NULL PRIMARY KEY,     AUTH_NAME CHARACTER VARYING(256),     AUTH_SRID INTEGER,     SRTEXT    CHARACTER VARYING(2048) ) 

In spatially enabled databases (such as IBM Db2, IBM Informix, Ingres, Microsoft SQL Server, MonetDB, MySQL, Oracle RDBMS, Teradata, PostGIS, SQL Anywhere and Vertica), SRIDs are used to uniquely identify the coordinate systems used to define columns of spatial data or individual spatial objects in a spatial column (depending on the spatial implementation). SRIDs are typically associated with a well-known text (WKT) string definition of the coordinate system (SRTEXT, above). Here are two common coordinate systems with their EPSG SRID value followed by their WKT:

UTM, Zone 17N, NAD27 — SRID 2029:

PROJCS["NAD27(76) / UTM zone 17N",     GEOGCS["NAD27(76)",         DATUM["North_American_Datum_1927_1976",             SPHEROID["Clarke 1866",6378206.4,294.9786982138982,                 AUTHORITY["EPSG","7008"]],             AUTHORITY["EPSG","6608"]],         PRIMEM["Greenwich",0,             AUTHORITY["EPSG","8901"]],         UNIT["degree",0.01745329251994328,             AUTHORITY["EPSG","9122"]],         AUTHORITY["EPSG","4608"]],     UNIT["metre",1,         AUTHORITY["EPSG","9001"]],     PROJECTION["Transverse_Mercator"],     PARAMETER["latitude_of_origin",0],     PARAMETER["central_meridian",-81],     PARAMETER["scale_factor",0.9996],     PARAMETER["false_easting",500000],     PARAMETER["false_northing",0],     AUTHORITY["EPSG","2029"],     AXIS["Easting",EAST],     AXIS["Northing",NORTH]] 

WGS84 — SRID 4326

GEOGCS["WGS 84",     DATUM["WGS_1984",         SPHEROID["WGS 84",6378137,298.257223563,             AUTHORITY["EPSG","7030"]],         AUTHORITY["EPSG","6326"]],     PRIMEM["Greenwich",0,         AUTHORITY["EPSG","8901"]],     UNIT["degree",0.01745329251994328,         AUTHORITY["EPSG","9122"]],     AUTHORITY["EPSG","4326"]] 

SRID values associated with spatial data can be used to constrain spatial operations — for instance, spatial operations cannot be performed between spatial objects with differing SRIDs in some systems, or trigger coordinate system transformations between spatial objects in others.

• Engineering datum
• Geodesy
• Geodetic datum
• Georeferencing
• Geographic coordinate systems
• Geographic information system (GIS).
• Grid reference
• Linear referencing
• List of National Coordinate Reference Systems
• Terms of orientation

Wikidata has the property:

• spatial reference system (P3037) (see uses)

• spatialreference.org – A website with more than 13000 spatial reference systems, in a variety of formats.
• OpenGIS Specifications (Standards) Archived 2004-12-13 at the Wayback Machine
• OpenGIS Simple Features Specification for CORBA (99-054)
• OpenGIS Simple Features Specification for OLE/COM (99-050)
• OpenGIS Simple Features Specification for SQL (99-054, 05-134, 06-104r3)
• OGR Archived 2006-04-22 at the Wayback Machine — library implementing relevant OGC standards
• EPSG.org - Official EPSG Geodetic Parameter Dataset webpage. Search engine for EPSG defined reference systems.
• EPSG.io/ - Full text search indexing over 6000 coordinate systems
• Galdos Systems INdicio CRS Registry