| Distribuzione Gamma |
|---|
Funzione di densità di probabilità
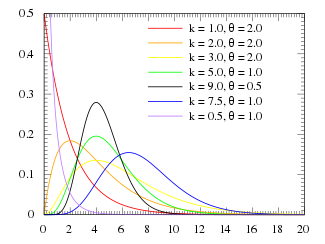 |
Funzione di ripartizione
 |
| Parametri |  e e 
oppure
 e e 
( , ,  ) ) |
|---|
| Supporto |  |
|---|
| Funzione di densità | 
(con  la funzione Gamma) la funzione Gamma) |
|---|
| Funzione di ripartizione | 
( è la funzione Gamma incompleta inferiore regolarizzata) è la funzione Gamma incompleta inferiore regolarizzata) |
|---|
| Valore atteso |  |
|---|
| Moda |  se se  |
|---|
| Varianza |  |
|---|
| Indice di asimmetria |  |
|---|
| Curtosi |  |
|---|
| Entropia | 
(con  la funzione digamma) la funzione digamma) |
|---|
| Funzione generatrice dei momenti |  per per  |
|---|
| Funzione caratteristica |  |
|---|
| Manuale |
In teoria delle probabilità la distribuzione Gamma è una distribuzione di probabilità continua, che comprende, come casi particolari, anche le distribuzioni esponenziale e chi quadrato.
Viene utilizzata come modello generale dei tempi di attesa nella teoria delle code, soprattutto qualora siano importanti effetti che rimuovano "l'assenza di memoria" della distribuzione esponenziale. Nella statistica bayesiana è comune sia come distribuzione a priori che come distribuzione a posteriori.
La distribuzione Gamma è la distribuzione di probabilità della variabile aleatoria definita come la somma di variabili aleatorie indipendenti e con distribuzione esponenziale; la distribuzione Gamma è una distribuzione di probabilità definita sui numeri reali positivi,  . A seconda degli autori, viene parametrizzata in due modi diversi: sia tramite la coppia di numeri positivi
. A seconda degli autori, viene parametrizzata in due modi diversi: sia tramite la coppia di numeri positivi  , sia tramite la coppia di numeri positivi
, sia tramite la coppia di numeri positivi  . Le due parametrizzazioni sono legate dalle relazioni
. Le due parametrizzazioni sono legate dalle relazioni  e
e  . Nel seguito si farà riferimento alla parametrizzazione Gamma
. Nel seguito si farà riferimento alla parametrizzazione Gamma .
.
La sua funzione di densità di probabilità è
 ,
,
dove  è la funzione Gamma di Eulero.
è la funzione Gamma di Eulero.
Possiamo osservare che se  vale che
vale che 
La sua funzione di ripartizione è la funzione gamma incompleta inferiore regolarizzata
 ,
,
dove  è la funzione Gamma incompleta inferiore.
è la funzione Gamma incompleta inferiore.
I momenti semplici della distribuzione Gamma di parametri  sono
sono
![{\displaystyle \mu _{n}=\mathbb {E} [X^{n}]={\tfrac {1}{\theta ^{k}\Gamma (k)}}\int _{0}^{\infty }x^{k+n-1}e^{-{\frac {x}{\theta }}}dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8277ca0c5f22c9f11b60902d64458169995ac72)

dove si effettua la solita sostituzione  per ottenere la rappresentazione integrale della funzione Gamma di Eulero.
per ottenere la rappresentazione integrale della funzione Gamma di Eulero.
In particolare la distribuzione ha:
- valore atteso
![{\displaystyle \mathbb {E} [X]=k\theta ;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cddf8c6de2a11a11f196f858b0f414cee055d86)
- varianza

- indice di asimmetria

- indice di curtosi

Funzione generatrice di momenti:
![{\displaystyle \mathbb {M} _{X}(t)=\mathbb {E} [e^{tX}]={\frac {1}{\theta ^{k}\Gamma (k)}}\int _{0}^{\infty }x^{k-1}e^{-x\left({\frac {1}{\theta }}-t\right)}dx={\frac {1}{\theta ^{k}\Gamma (k)({\tfrac {1}{\theta }}-t)^{k}}}\int _{0}^{\infty }u^{k-1}e^{-u}du}](https://wikimedia.org/api/rest_v1/media/math/render/svg/229dbeb785cca82ca8dea2623c941173a8164f12)
 che esiste per ogni valore di t tale che
che esiste per ogni valore di t tale che 
Se  segue la distribuzione Gamma
segue la distribuzione Gamma allora
allora  segue la distribuzione Gamma
segue la distribuzione Gamma .
.
Se  sono variabili aleatorie indipendenti, ognuna con distribuzione Gamma
sono variabili aleatorie indipendenti, ognuna con distribuzione Gamma , allora la loro somma
, allora la loro somma  segue la distribuzione Gamma
segue la distribuzione Gamma .
.
La distribuzione Gamma generalizza diverse distribuzioni (è conveniente ora utilizzare la seconda delle due parametrizzazioni presentate):
Nell'inferenza bayesiana la distribuzione Gamma può descrivere sia a priori che a posteriori di un'osservazione il parametro  di diverse distribuzioni di probabilità, ad esempio della distribuzione esponenziale e della distribuzione di Poisson.
di diverse distribuzioni di probabilità, ad esempio della distribuzione esponenziale e della distribuzione di Poisson.
La distribuzione Gamma inversa è la distribuzione dell'inversa  di una variabile aleatoria
di una variabile aleatoria  che segue la distribuzione Gamma.
che segue la distribuzione Gamma.
Se  e
e  sono variabili aleatorie indipendenti con distribuzioni
sono variabili aleatorie indipendenti con distribuzioni  e
e  , allora
, allora  segue la distribuzione Beta
segue la distribuzione Beta  , mentre
, mentre  segue una distribuzione Beta del secondo tipo.
segue una distribuzione Beta del secondo tipo.
Più in generale il vettore  , descritto da
, descritto da  variabili aleatorie indipendenti
variabili aleatorie indipendenti  di distribuzioni
di distribuzioni  , segue una distribuzione di Dirichlet di parametri
, segue una distribuzione di Dirichlet di parametri  .
.
Una generalizzazione della distribuzione Gamma è la distribuzione di Wishart, che generalizza anche la distribuzione  .
.
Calcoliamo ora degli stimatori che possano, dato un campione presumibilmente Gamma distribuito, restituirci una stima dei suoi parametri  e
e  .
.
Uno stimatore corretto per  è
è

Stimatore asintoticamente corretto per  è:
è:
![{\displaystyle {\hat {k}}=\psi _{0}^{-1}\left[\ln \left({\sqrt[{n}]{\prod _{i=1}^{n}{\frac {x_{i}}{\theta }}}}\right)\right]=\psi _{0}^{-1}\left[{\frac {1}{n}}\sum _{i=1}^{n}\ln \left({\frac {x_{i}}{\theta }}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/164a62cbd805287c5254b7a8ac721ae783ba8a40)
dove  è la funzione inversa della funzione digamma
è la funzione inversa della funzione digamma  così definita:
così definita:

Le dimostrazioni adottano il metodo della massima verosimiglianza, dove la funzione di verosimiglianza dato il campione è


Il parametro  è il più semplice da stimare.
è il più semplice da stimare.
Notiamo che la funzione di verosimiglianza è ovunque positiva e nel limite degli estremi di  , si annulla.
, si annulla.


Pertanto se imponiamo la sua derivata uguale a zero, nel caso la soluzione sia unica, questa deve per forza essere un punto di massimo.

Occorre adesso eguagliare a zero tale espressione

Ed ecco il nostro stimatore di  , che ricorda molto una media aritmetica, riscalata sul parametro
, che ricorda molto una media aritmetica, riscalata sul parametro  (che ricordiamo essere uguale a 1 nel caso particolare della distribuzione esponenziale). Si può notare facilmente che il valor atteso di questo stimatore è proprio
(che ricordiamo essere uguale a 1 nel caso particolare della distribuzione esponenziale). Si può notare facilmente che il valor atteso di questo stimatore è proprio  , data la linearità dell'operatore.
, data la linearità dell'operatore.
![{\displaystyle \mathbb {E} [{\hat {\theta }}]=\mathbb {E} \left[{\frac {1}{kn}}\sum _{i=1}^{n}x_{i}\right]={\frac {1}{kn}}\sum _{i=1}^{n}\mathbb {E} [x_{i}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b17e7bf8b4676ee4d7967b301f3f8413b7b02a9)
Ricordiamo ![{\displaystyle \mathbb {E} [x_{i}]=k\theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3289a103aee025bd8c594d8e8b41596669d3405f)
![{\displaystyle \mathbb {E} [{\hat {\theta }}]={\frac {nk\theta }{kn}}=\theta .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f4f1a84738b0b7d1becb023f6bb6b9ecaa96c3c)
Prendiamo ora in esame il calcolo dello stimatore per  .
.
Anche qui la funzione di verosimiglianza si annulla per il limite di  e
e  , pertanto procediamo con il calcolo della derivata.
, pertanto procediamo con il calcolo della derivata.
![{\displaystyle \left({\frac {\partial {\mathcal {L}}}{\partial k}}\right)_{k={\hat {k}}}\!\!\!\!\!=e^{-{\frac {1}{\theta }}\sum x_{i}}\left(\prod x_{i}\right)^{{\hat {k}}-1}\left[{\frac {\ln \left(\prod x_{i}\right)}{\theta ^{n{\hat {k}}}\Gamma ^{n}({\hat {k}})}}-n{\frac {\ln(\theta )+\psi _{0}({\hat {k}})}{\theta ^{n{\hat {k}}}\Gamma ^{n}({\hat {k}})}}\right]={\frac {e^{-{\frac {1}{\theta }}\sum x_{i}}\left(\prod x_{i}\right)^{{\hat {k}}-1}}{\theta ^{n{\hat {k}}}\Gamma ^{n}({\hat {k}})}}\left[\ln \left(\prod {\frac {x_{i}}{\theta }}\right)-n\psi _{0}({\hat {k}})\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ddd482df97be2595f9ca0773936961a85e54341)
Con  indichiamo la funzione digamma così definita:
indichiamo la funzione digamma così definita:

che può essere espressa mediante una relazione integrale

Eguagliando a zero la nostra funzione di verosimiglianza otteniamo il nostro punto di massimo
![{\displaystyle \left({\frac {\partial {\mathcal {L}}}{\partial k}}\right)_{k={\hat {k}}}\!\!\!\!\!=0\,\Rightarrow \,\ln \left(\prod {\frac {x_{i}}{\theta }}\right)-n\psi _{0}({\hat {k}})=0\,\Rightarrow \,\psi _{0}({\hat {k}})=\ln \left({\sqrt[{n}]{\prod {\frac {x_{i}}{\theta }}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3f390a9219c7dc1a3fab01b1535dd05814c3fb5)
La funzione digamma, nei reali positivi è strettamente crescente, per cui esiste la funzione inversa
![{\displaystyle {\hat {k}}=\psi _{0}^{-1}\left[\ln \left({\sqrt[{n}]{\prod _{i=1}^{n}{\frac {x_{i}}{\theta }}}}\right)\right]=\psi _{0}^{-1}\left[{\frac {1}{n}}\sum _{i=1}^{n}\ln \left({\frac {x_{i}}{\theta }}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/164a62cbd805287c5254b7a8ac721ae783ba8a40)
Questo stimatore ottenuto è asintoticamente corretto, ma per valori finiti andrebbe verificato il suo valore atteso che, se risultasse essere  , allora sarebbe un corretto stimatore.
, allora sarebbe un corretto stimatore.
Calcoliamo quindi
![{\displaystyle \mathbb {E} [\psi _{0}({\hat {k}})]=\mathbb {E} \left[{\frac {1}{n}}\sum _{i=1}^{n}\ln \left({\frac {x_{i}}{\theta }}\right)\right]={\frac {1}{n}}\sum _{i=1}^{n}\mathbb {E} \left[\ln \left({\frac {x_{i}}{\theta }}\right)\right]={\frac {1}{n}}\sum _{i=1}^{n}\int _{0}^{\infty }\ln \left({\frac {x_{i}}{\theta }}\right){\frac {x_{i}^{k-1}}{\theta ^{k}\Gamma (k)}}e^{-{\frac {x_{i}}{\theta }}}dx_{i},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c8bc6cbbd89a2d13aaba1d276ae22c098b14765)
dove abbiamo usato la linearità del valore atteso e scritto la sua definizione su variabile aleatoria continua.
![{\displaystyle \mathbb {E} [\psi _{0}({\hat {k}})]={\frac {1}{n\theta ^{k}\Gamma (k)}}\sum _{i=1}^{n}\int _{0}^{\infty }\ln \left({\frac {x_{i}}{\theta }}\right)x_{i}^{k-1}e^{-{\frac {x_{i}}{\theta }}}dx_{i}={\frac {1}{\theta ^{k}\Gamma (k)}}\int _{0}^{\infty }\ln \left({\frac {t}{\theta }}\right)t^{k-1}e^{-{\frac {t}{\theta }}}dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06d3bad1bfe68c7c540d2be4675258b12c5448f7)
Tutti gli integrali nella  -esima variabile sono uguali tra di loro, quindi la loro somma dà
-esima variabile sono uguali tra di loro, quindi la loro somma dà  volte il singolo integrale nella generica variabile di integrazione
volte il singolo integrale nella generica variabile di integrazione  .
.
![{\displaystyle \mathbb {E} [\psi _{0}({\hat {k}})]={\frac {1}{\theta ^{k}\Gamma (k)}}\int _{0}^{\infty }\ln \left({\frac {t}{\theta }}\right)t^{k-1}e^{-{\frac {t}{\theta }}}dt={\frac {\theta ^{k-1}}{\theta ^{k-1}\Gamma (k)}}\int _{0}^{\infty }\ln(u)u^{k-1}e^{-u}du={\frac {1}{\Gamma (k)}}\int _{0}^{\infty }u^{k-1}\ln(u)e^{-u}du}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf449f93bd4efe7c443fa41cd0b6ffdd355b095f)
e il risultato di quest'ultimo integrale è proprio  per qualunque
per qualunque  con parte reale positiva. Abbiamo quindi ottenuto l'identità
con parte reale positiva. Abbiamo quindi ottenuto l'identità
![{\displaystyle \mathbb {E} [\psi _{0}({\hat {k}})]=\psi _{0}(k),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbd20b00a6cac6593dc6497d5761c22f3ec4c0ba)
che non è sufficiente a dire che lo stimatore sia corretto (non solo asintoticamente), ma è tuttavia necessario.
In effetti dalla disuguaglianza di Jensen (secondo cui ![{\displaystyle \varphi (\mathbb {E} [X])\leq \mathbb {E} [\varphi (X)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d34ce6476ae519e75fd57c640cb73cfd680b69c1) per una qualunque variabile aleatoria X e una funzione convessa
per una qualunque variabile aleatoria X e una funzione convessa  ) si ottiene un risultato più forte grazie al fatto che la funzione
) si ottiene un risultato più forte grazie al fatto che la funzione  è convessa su tutto il suo dominio.
è convessa su tutto il suo dominio.
Infatti usando la disuguaglianza di Jensen per  e
e  risulterà
risulterà
![{\displaystyle \psi _{0}^{-1}\left(\mathbb {E} \left[\psi _{0}({\hat {k}})\right]\right)\leq \mathbb {E} \left[\psi _{0}^{-1}\left(\psi _{0}({\hat {k}})\right)\right]=\mathbb {E} [{\hat {k}}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9a4911c2a2aba3bb77488949042223ca8daa58b)
Dall'uguaglianza ottenuta in precedenza il membro di sinistra si semplifica così da avere:
![{\displaystyle k\leq \mathbb {E} [{\hat {k}}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c026e53d32c0cca9e16d627b86c8848f71cbb6c8)



 Wikimedia Commons contiene immagini o altri file su distribuzione Gamma
Wikimedia Commons contiene immagini o altri file su distribuzione Gamma































![{\displaystyle \mu _{n}=\mathbb {E} [X^{n}]={\tfrac {1}{\theta ^{k}\Gamma (k)}}\int _{0}^{\infty }x^{k+n-1}e^{-{\frac {x}{\theta }}}dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8277ca0c5f22c9f11b60902d64458169995ac72)


![{\displaystyle \mathbb {E} [X]=k\theta ;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cddf8c6de2a11a11f196f858b0f414cee055d86)



![{\displaystyle \mathbb {M} _{X}(t)=\mathbb {E} [e^{tX}]={\frac {1}{\theta ^{k}\Gamma (k)}}\int _{0}^{\infty }x^{k-1}e^{-x\left({\frac {1}{\theta }}-t\right)}dx={\frac {1}{\theta ^{k}\Gamma (k)({\tfrac {1}{\theta }}-t)^{k}}}\int _{0}^{\infty }u^{k-1}e^{-u}du}](https://wikimedia.org/api/rest_v1/media/math/render/svg/229dbeb785cca82ca8dea2623c941173a8164f12)






























![{\displaystyle {\hat {k}}=\psi _{0}^{-1}\left[\ln \left({\sqrt[{n}]{\prod _{i=1}^{n}{\frac {x_{i}}{\theta }}}}\right)\right]=\psi _{0}^{-1}\left[{\frac {1}{n}}\sum _{i=1}^{n}\ln \left({\frac {x_{i}}{\theta }}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/164a62cbd805287c5254b7a8ac721ae783ba8a40)









![{\displaystyle \mathbb {E} [{\hat {\theta }}]=\mathbb {E} \left[{\frac {1}{kn}}\sum _{i=1}^{n}x_{i}\right]={\frac {1}{kn}}\sum _{i=1}^{n}\mathbb {E} [x_{i}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b17e7bf8b4676ee4d7967b301f3f8413b7b02a9)
![{\displaystyle \mathbb {E} [x_{i}]=k\theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3289a103aee025bd8c594d8e8b41596669d3405f)
![{\displaystyle \mathbb {E} [{\hat {\theta }}]={\frac {nk\theta }{kn}}=\theta .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f4f1a84738b0b7d1becb023f6bb6b9ecaa96c3c)


![{\displaystyle \left({\frac {\partial {\mathcal {L}}}{\partial k}}\right)_{k={\hat {k}}}\!\!\!\!\!=e^{-{\frac {1}{\theta }}\sum x_{i}}\left(\prod x_{i}\right)^{{\hat {k}}-1}\left[{\frac {\ln \left(\prod x_{i}\right)}{\theta ^{n{\hat {k}}}\Gamma ^{n}({\hat {k}})}}-n{\frac {\ln(\theta )+\psi _{0}({\hat {k}})}{\theta ^{n{\hat {k}}}\Gamma ^{n}({\hat {k}})}}\right]={\frac {e^{-{\frac {1}{\theta }}\sum x_{i}}\left(\prod x_{i}\right)^{{\hat {k}}-1}}{\theta ^{n{\hat {k}}}\Gamma ^{n}({\hat {k}})}}\left[\ln \left(\prod {\frac {x_{i}}{\theta }}\right)-n\psi _{0}({\hat {k}})\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ddd482df97be2595f9ca0773936961a85e54341)


![{\displaystyle \left({\frac {\partial {\mathcal {L}}}{\partial k}}\right)_{k={\hat {k}}}\!\!\!\!\!=0\,\Rightarrow \,\ln \left(\prod {\frac {x_{i}}{\theta }}\right)-n\psi _{0}({\hat {k}})=0\,\Rightarrow \,\psi _{0}({\hat {k}})=\ln \left({\sqrt[{n}]{\prod {\frac {x_{i}}{\theta }}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3f390a9219c7dc1a3fab01b1535dd05814c3fb5)
![{\displaystyle \mathbb {E} [\psi _{0}({\hat {k}})]=\mathbb {E} \left[{\frac {1}{n}}\sum _{i=1}^{n}\ln \left({\frac {x_{i}}{\theta }}\right)\right]={\frac {1}{n}}\sum _{i=1}^{n}\mathbb {E} \left[\ln \left({\frac {x_{i}}{\theta }}\right)\right]={\frac {1}{n}}\sum _{i=1}^{n}\int _{0}^{\infty }\ln \left({\frac {x_{i}}{\theta }}\right){\frac {x_{i}^{k-1}}{\theta ^{k}\Gamma (k)}}e^{-{\frac {x_{i}}{\theta }}}dx_{i},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c8bc6cbbd89a2d13aaba1d276ae22c098b14765)
![{\displaystyle \mathbb {E} [\psi _{0}({\hat {k}})]={\frac {1}{n\theta ^{k}\Gamma (k)}}\sum _{i=1}^{n}\int _{0}^{\infty }\ln \left({\frac {x_{i}}{\theta }}\right)x_{i}^{k-1}e^{-{\frac {x_{i}}{\theta }}}dx_{i}={\frac {1}{\theta ^{k}\Gamma (k)}}\int _{0}^{\infty }\ln \left({\frac {t}{\theta }}\right)t^{k-1}e^{-{\frac {t}{\theta }}}dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06d3bad1bfe68c7c540d2be4675258b12c5448f7)


![{\displaystyle \mathbb {E} [\psi _{0}({\hat {k}})]={\frac {1}{\theta ^{k}\Gamma (k)}}\int _{0}^{\infty }\ln \left({\frac {t}{\theta }}\right)t^{k-1}e^{-{\frac {t}{\theta }}}dt={\frac {\theta ^{k-1}}{\theta ^{k-1}\Gamma (k)}}\int _{0}^{\infty }\ln(u)u^{k-1}e^{-u}du={\frac {1}{\Gamma (k)}}\int _{0}^{\infty }u^{k-1}\ln(u)e^{-u}du}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf449f93bd4efe7c443fa41cd0b6ffdd355b095f)

![{\displaystyle \mathbb {E} [\psi _{0}({\hat {k}})]=\psi _{0}(k),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbd20b00a6cac6593dc6497d5761c22f3ec4c0ba)
![{\displaystyle \varphi (\mathbb {E} [X])\leq \mathbb {E} [\varphi (X)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d34ce6476ae519e75fd57c640cb73cfd680b69c1)




![{\displaystyle \psi _{0}^{-1}\left(\mathbb {E} \left[\psi _{0}({\hat {k}})\right]\right)\leq \mathbb {E} \left[\psi _{0}^{-1}\left(\psi _{0}({\hat {k}})\right)\right]=\mathbb {E} [{\hat {k}}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9a4911c2a2aba3bb77488949042223ca8daa58b)
![{\displaystyle k\leq \mathbb {E} [{\hat {k}}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c026e53d32c0cca9e16d627b86c8848f71cbb6c8)
