余等化子

圏論における余等化子(よとうかし、英: coequalizer , coequaliser)は同値関係による商の、任意の圏における対象に対する一般化である。余等化子は等化子の双対となる圏論的構成である。
定義
[編集]余等化子は二つの対象 X, Y と二つの平行射 f, g: X → Y からなる図式の余極限である。より明示的に書けば、余等化子は対象 Q と射 q: Y → Q で q ∘ f = q ∘ g を満たすものの組として定義することができる。さらに言えば、対 (Q, q) は、同じ性質を持つ別の対 (Q', q') が与えられたとき、以下の図式
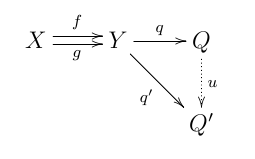
を可換とする射 u: Q → Q' が一意に存在するという意味での普遍性を持たなければならない。全ての普遍構成がそうである通り、余等化子は存在すれば同型を除いて一意である(それがゆえに、与えられた平行射の単に (the) 余等化子と呼ぶことに混乱の虞は無い)。
余等化子 q が任意の圏において全型射であることを示すことができる。
例
[編集]- 集合の圏において、二つの写像 f, g: X → Y の余等化子は、f(x) ∼ g(x) (∀x ∈ X) を満たす最小の同値関係 ∼ による Y の商である[1]。特に R が集合 Y 上の同値関係で、その各成分への射影 r1, r2: (Y × Y ⊃) R → Y を取れば、r1, r2 の余等化子は商集合 Y/R にちょうど一致する。
- 群の圏における余等化子も非常によく似ている。f, g: X → Y が二つの群準同型とすれば、それらの余等化子は集合 S = {f(x)g(x)−1 | x ∈ X} の生成する正規部分群で割った Y の商群である。
- アーベル群の場合は特に単純で、余等化子は剰余群 Y / im(f – g)、すなわち群準同型 f − g の余核に等しい(後述)。
- 位相空間の圏において円周対象 S1 は標準 0-単体から標準 1-単体への二つの包含射の余等化子と見ることができる。
- 余等化子の全体は大きくなりうる。ただ一つの対象とその上の恒等射のみを持つ圏 1 からただ二つの対象とその間の非自明な射がちょうど一つ存在する圏 2 への函手はちょうど二つ存在する。それら二つの函手の余等化子は、自然数全体が加法に関して成すモノイドを単一対象圏と見たものに一致する。特に、このことから任意の余等化射は圏論的全射となることが分かるが、これは必ずしも集合論的全射でない。
性質
[編集]- 任意の余等化子はエピである。
- トポスにおいて任意のエピ射はその核対の余等化子となる。
特別の場合
[編集]零射を持つ圏において射 f の余核が f と平行な零射との余等化子として定義できる。
前加法圏において射の和と差が意味を持つ(射集合が実際にアーベル群を成す)。そのような圏において、二つの射 f, g の余等化子はそれらの差の余核として
- coeq(f, g) = coker(g – f)
で定義できる。
より強い概念として絶対余等化子 (absolute coequalizer) がある。これは任意の函手の下で不変な余等化子を言う。厳密に言えば、圏 𝒞 における対 f, g: X → Y の絶対余等化子は、上記の通り定められる余等化子 (Q, q) であって、更なる性質として任意の函手 F: 𝒞 → 𝒟 に対して (F(Q), F(q)) は圏 𝒟 における対 F(f), F(g) の余等化子となるという条件を満足する。分裂余等化子は絶対余等化子の例である。
関連項目
[編集]注意
[編集]- ^ Barr, Michael; Wells, Charles (1998) (PDF). Category theory for computing science. p. 278 2013年7月25日閲覧。
参考文献
[編集]- Saunders Mac Lane: Categories for the Working Mathematician, Second Edition, 1998.
- Coequalizers - page 65
- Absolute coequalizers - page 149
外部リンク
[編集]- Interactive Web page which generates examples of coequalizers in the category of finite sets. Written by Jocelyn Paine.