標準模型

この記事は中立的な観点に基づく疑問が提出されているか、議論中です。 (2011年12月) |
この記事の正確性に疑問が呈されています。 |
| 標準模型 | ||||||||
|---|---|---|---|---|---|---|---|---|
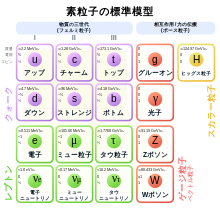 | ||||||||
| 標準模型の素粒子 | ||||||||
| ||||||||
標準模型(ひょうじゅんもけい、英: Standard Model、略称: SM)とは、素粒子物理学において、強い相互作用、弱い相互作用、電磁相互作用の3つの基本的な相互作用を記述するためのモデルのひとつである。
標準理論(ひょうじゅんりろん)または標準モデル(ひょうじゅんモデル)とも言う。多くの物理現象をほぼ的確に描写する仮説である。
概要
[編集]標準模型は、強い相互作用についての量子色力学、弱い相互作用と電磁相互作用についてのワインバーグ=サラム理論をあわせた SU(3)c×SU(2)L×U(1)Y ゲージ対称性を基礎とし、ヒッグス機構による真空の対称性の破れとフェルミオンの質量獲得、アノマリーの相殺の要請によるフェルミオンの世代構造と世代間混合とCP対称性の破れについての小林・益川理論などの理論も組み込まれたものである[1]。標準模型は特殊相対性理論と整合する量子論として、場の量子論的方法で記述され、今のところ重力をのぞき、場の量子論であつかわれるあらゆる事象を的確に描写している[2]。
標準模型の素粒子
[編集]標準模型の素粒子は力を媒介するスピン1のゲージ粒子、対称性を破るスピン0のヒッグス粒子、物質を構成するスピン1/2のフェルミオンからなる。
ゲージ粒子
[編集]| 粒子名 | 記号 | ゲージ対称性 |
|---|---|---|
| グルーオン | G | SU(3)c |
| Wボソン | W | SU(2)L×U(1)Y |
| Zボソン | Z | |
| 光子 | A |
標準模型はヤン=ミルズ理論に従い、それぞれのゲージ群に対応するゲージ粒子が存在する。
SU(3)Cに対応するゲージ粒子はグルーオンと呼ばれている。
SU(2)LとU(1)Yに対応するゲージ粒子に関しては、ヒッグス機構によりゲージ場の混合と質量の獲得が起こるので、多少複雑な様相を呈する。ウィークアイソスピン SU(2)L の非対角成分は質量を獲得してWボソンとなり、対角成分とウィークハイパーチャージ U(1)Y は交じり合って、質量を獲得するZボソンと質量を獲得しない光子になる。
フェルミオン
[編集]| 粒子名 | 記号 | 表現 |
|---|---|---|
| クォーク | Q | (3,2)1/6 |
| 上系列反クォーク | U | (3*,1)-2/3 |
| 下系列反クォーク | D | (3*,1)1/3 |
| レプトン | L | (1,2)-1/2 |
| 反荷電レプトン | E | (1,1)1 |
フェルミオンは強い相互作用をするクォークと、強い相互作用をしないレプトンに分けられる。さらに、クォークとレプトンは、それぞれ左手型(left-handed)粒子と右手型(right-handed)粒子に分類することができる。標準模型における左手型粒子は電弱相互作用のウィークアイソスピンを持つが、右手型粒子は持たない。そのため、左手型粒子と右手型粒子ではゲージ相互作用の形が異なり、標準模型はゲージ相互作用に関してカイラルな理論となっている。また、この性質のために、電弱対称性がヒッグス機構によって破れないかぎり、全てのクォークとレプトンは質量を持つことができない。全てのクォークと荷電レプトンは、ヒッグス機構によって質量を獲得する。ニュートリノは標準模型の範囲内では質量を持つことはない
フェルミオンは左手型クォークと左手型レプトン、右手型アップクォークと右手型ダウンクォーク、右手型荷電レプトンで世代と呼ばれるグループを構成する。一般に、ゲージ相互作用を含む模型については、カイラルアノマリーと重力アノマリーが相殺されている必要があるが、世代を構成するフェルミオンの間でアノマリーが相殺される構成になっている。標準模型は、3世代のクォークとレプトンが存在する。小林・益川理論によると、フェルミオンの混合によりCP対称性が破れるためには3世代以上のフェルミオンが必要である。実際に、フェルミオンの混合に起因するCP対称性の破れは実験で確認されており、標準模型による予言と良く一致することが確かめられている。
ヒッグス粒子
[編集]標準模型では、ヒッグス機構により電弱対称性が自発的に破れる。一般に場の揺らぎは粒子として解釈されるが、ヒッグス場の4つある揺らぎの自由度のうち3つは、WボソンとZボソンが質量を持つことに伴い、その縦波成分として吸収される。残りの1自由度は、スピン0のスカラー粒子であるヒッグス粒子としてあらわれる。2012年7月にジュネーブ郊外の欧州原子核研究機構 (CERN) で行われているLHC実験により新粒子の発見が発表された[3]。この新粒子の性質はヒッグス粒子と良く一致しており、その後のスピン-パリティ観測、崩壊後粒子の信号強度の検証により標準模型におけるヒッグス粒子、およびこれを内包する理論によるヒッグス粒子であることが認定された。
歴史
[編集]
- 1928年 - ポール・ディラックが相対論的量子力学により、電子の反粒子の存在を予言(ディラック自身はこの粒子を陽子と解釈しようとした)
- 1931年 - ヴォルフガング・パウリがニュートリノの存在を予言
- 1932年 - カール・デイヴィッド・アンダーソンにより、電子の反粒子である陽電子が発見された
- 1948年 - 朝永振一郎、リチャード・P・ファインマン、ジュリアン・シュウィンガーによる量子電磁力学の繰り込みの発表
- 1954年 - 楊振寧、ロバート・ミルズによりヤン・ミルズ理論が発表された[4]。
- 1956年 -
- 1957年 - 呉健雄らのグループがコバルト60のベータ崩壊においてパリティが破れていることを観測した(ウーの実験)[7]。
- 1964年 -
- 1967年 - スティーブン・ワインバーグにより後のワインバーグ=サラム理論が発表された[11]。(1968年にアブドゥッサラームも独立に発表[12]。)
- 1971年 - ヘーラルト・トホーフト、マルティヌス・フェルトマンがヤン・ミルズ理論の繰り込みに成功[13][14]。
- 1973年 -
- 小林誠と益川敏英により小林・益川理論が提唱された[15]。
- デイビッド・グロスとフランク・ウィルチェック[16]、H. デビッド・ポリツァー[17]による漸近的自由性の発見
- ガーガメル実験により、中性カレント反応(Zボゾンを介した相互作用)が発見された。
- 1974年 - サミュエル・ティンらのグループ[18]、バートン・リヒターらのグループ[19]により、独立にジェイプサイ中間子(チャームクォーク)が発見された(11月革命)
- 1977年 - レオン・レーダーマンらのグループにより、ウプシロン中間子(ボトムクォーク)が発見された[20]。
- 1983年 - カルロ・ルビア、シモン・ファンデルメールらのグループにより、Wボソン[21]、Zボソン[22]の発見
- 1995年 - テバトロン実験により、トップクォークが発見された[23][24]。
- 2012年 - LHC実験によりヒッグス粒子が発見された[25][26]

未解決の問題
[編集]標準模型は2014年現在までに行われた素粒子物理学に関する実験結果をほとんど全て矛盾することなく説明することができているが、その一方で、理論的または実験・観測的観点から解決すべき問題をいくつか抱えている。このことは標準模型を超える物理の存在を示唆する。この節では標準模型において未解決の問題を列挙する。
重力の量子化
[編集]標準模型は基本的な相互作用とされる4つの力のうち、電磁気力、弱い力、強い力の3つをヤン=ミルズ理論に基づき量子論的に記述することに成功している。しかし、残りの1つである重力についてはその記述を欠いている。言い換えれば、重力を媒介するとされる重力子は標準模型の粒子のリストに含まれていない。これは、標準模型の基礎的な枠組みとなっている場の量子論における量子効果による発散の相殺を重力理論に適用できないからである。重力を量子論的に扱うことができる枠組みの候補としては、超弦理論、ループ量子重力理論などが挙げられる。
大統一理論
[編集]標準模型が記述する3つの力のうち、強い力は、電磁気力と弱い力とは別のゲージ対称性により記述されている。このため、3つの力を統一的に理解することは難しい。しかし、電磁気力を記述するU(1)ゲージ対称性がゲージ対称性がヒッグス機構により自発的に破れた結果あらわれたものであるように、標準模型のゲージ対称性もより大きなゲージ対称性が自発的に破れた結果あらわれたものである可能性が指摘されている。この可能性に基づいた理論は大統一理論と呼ばれている。のおおもととなった大統一理論のゲージ対称性にはいくつか候補があるが、SU(5)、SO(10)、などが提案されている。強い力と電弱相互作用を統一的に記述する大統一理論では、クォークをレプトンに変換するような相互作用が可能になる。具体的な現象としては陽子崩壊が予言される。カミオカンデなどの実験で陽子崩壊を実証するための実験が続けられているが、2014年現在、実験的証拠は得られていない。
階層性問題(fine tuning問題)
[編集]標準模型は場の量子論に基づいた模型であるため、物理的に意味のある量を計算するために繰り込みと呼ばれる操作が必要となる。このことと関連して、標準模型ではヒッグス機構による電弱対称性の自発的破れの大きさを観測事実と合わせるために、理論のパラメーターを非常に精密に調整する必要がある。この問題は、プランクスケール(1019 GeV)と電弱対称性が破れるスケール(102 GeV)の間に大きな隔たりがあることに起因しており階層性問題と呼ばれている。この問題を解決する模型として提案されているものはいくつかあるが、代表的なものの1つが超対称性模型である。
強いCP問題
[編集]中性子の電気双極子モーメントの測定により、その大きさは2014年現在の観測精度を下回る値であることが分かっている。このことは、標準模型の弱い相互作用以外の部分でCP対称性がよく成り立っていることを示しており、強い相互作用に関するパラメーターとクォークの湯川行列の位相がCP対称性がよく成り立つような値に設定されていることを意味している。標準模型ではこの2つのパラメーターは特に関連性の無いものであり、精密に調整されているという状況は不自然である。この不自然さの問題は何らかの機構によって解決されるべきであると考えられており、強いCP問題と呼ばれている。解決策の一つとして有力視されているものが、ペッチャイ・クイン機構である。この機構によりアクシオンと呼ばれる新しい粒子の存在が予言される。
世代構造の謎
[編集]標準模型のフェルミオンはヒッグスの真空期待値との結合(俗に湯川結合という)により質量を獲得しているが3世代が独立に結合しているわけではない。たとえば荷電レプトンの1世代と2世代とヒッグスという3点結合が存在し、3世代合わせると3×3行列として書ける質量行列として質量を得ている。この質量行列を対角化した後の質量固有状態として物理的なモード、すなわち電子やミュー粒子などのモードが書ける。標準模型の質量行列の要素はフリーパラメータとなっており、その値には数桁の開きがある。またレプトンとクォークでは質量行列の構造が大きく違い、レプトンの質量行列では非対角要素が大きく、クォークの質量行列では非対角要素が比較的小さい値を取っている。すなわち標準模型を使って現実の粒子描像を記述するためには質量パラメータに微細な調整が必要になってくる。この構造を対称性やオーダー1のパラメータを用いた理論から再現する研究が広く進められている。
標準模型における世代を俗にフレーバー(flavor)と呼び、フレーバー構造(flavor structure)、フレーバー物理(flavor physics)、フレーバー混合(flavor mixing)等の呼称で広まっている。
ニュートリノ振動
[編集]1998年に神岡鉱山に設置されたスーパーカミオカンデによりニュートリノ振動が発見された[27]が、これは質量を持ったニュートリノが存在することの証明となっている。標準模型ではニュートリノの質量は厳密に0であるため、この実験結果は標準模型には何らかの修正が必要であることを示すものの一つとして重要である。単純にニュートリノの質量項を標準模型の枠組みに加える場合は右巻きニュートリノを導入すればよいが、標準模型の荷電を用いると右巻きニュートリノはマヨラナ粒子となり右巻きニュートリノだけで組む質量項(マヨラナ質量項)が現れ、質量構造が複雑化する。これを取り入れた枠組みとして代表的なものの一つがシーソー機構である。
暗黒物質
[編集]現在の宇宙のエネルギー密度の約4分の1を暗黒物質が占めていることが明らかになっているが、標準模型には暗黒物質の候補となる粒子が存在しない。そのため、暗黒物質の正体を素粒子に求める場合は標準模型の拡張が必要である。仮説上の粒子として、通常の物質と暗黒物質を繋ぐ役割を持つ「Z’ボゾン」、その他「アクシオン」等が考えられている。2020年現在は未発見である”超対称性粒子”の中の「ゲージーノ」や「ヒグシーノ」の一部が暗黒物質の候補として挙げられている。
バリオン数の非対称性
[編集]標準模型に含まれるフェルミオンは粒子と反粒子の2種類に分類される。粒子と反粒子はほぼ対等な存在であるが我々の住む宇宙では粒子の量が反粒子に比べて多い。この非対称性はバリオン数の非対称性として知られている。標準模型はヒッグスとフェルミオンの結合を通してCP対称性の破れを引き起こすことが可能であり、これにより粒子・反粒子数の非対称性を生み出せることが知られているが、標準模型の持つ位相だけでは十分なバリオン数を作り出すことが出来ないことが知られており[28]標準模型を超える物理の存在を示唆していると考えられている。
ミューオンの歳差運動のずれ
[編集]2001年、ブルックヘブン国立研究所は、ミューオンの歳差運動が、標準模型の予測からずれている実験結果を報告した。2021年にフェルミ国立加速器研究所のミューオンg-2実験でも同様の結果が示された[29][30]。
脚注
[編集]- ^ 南部 et al. 3章(牧二郎 著)
- ^ C・ロヴェッリ『すごい物理学講義』河出文庫、2019年、168頁。
- ^ “Latest update in the search for the Higgs boson”. CERN. (4 July 2012) 4 July 2012閲覧。
- ^ Chen-Ning Yang and Robert L. Mills (1954). “Conservation of Isotopic Spin and Isotopic Gauge Invariance”. Physical Review 96: 191. doi:10.1103/PhysRev.96.191.
- ^ T. D. Lee and Chen-Ning Yang (1956). “Question of Parity Conservation in Weak Interactions”. Physical Review 104: 254. doi:10.1103/PhysRev.104.254.
- ^ C. L. Cowan, F. Reines, F. B. Harrison, H. W. Kruse and A. D. McGuire (1956). “Detection of the free neutrino: A Confirmation”. Science 124: 103. doi:10.1126/science.124.3212.103.
- ^ C. S. Wu, E. Ambler, R. W. Harvard, D. D. Hoppes and R. P. Hudson (1957). “Experimental Test Of Parity Conservation In Beta Decay”. Physical Review 105: 1413. doi:10.1103/PhysRev.105.1413.
- ^ J. H. Christenson, J. W. Cronin, V. L. Fitch and R. Turlay (1964). “Evidence for the 2 pi Decay of the k(2)0 Meson”. Physical Review Letters 13: 138. doi:10.1103/PhysRevLett.13.138.
- ^ Murrey Gell-Mann (1964). “A Schematic Model of Baryons and Mesons”. Physics Letters 8: 214. doi:10.1016/S0031-9163(64)92001-3.
- ^ Peter W. Higgs (1964). “Broken symmetries, massless particles and gauge fields”. Physics Letters 12: 132. doi:10.1016/0031-9163(64)91136-9.
- ^ Steven Weiberg (1967). “A Model of Leptons”. Physical Review Letters 19: 1264. doi:10.1103/PhysRevLett.19.1264.
- ^ Abdus Salam (1968). “Weak and Electromagnetic Interactions”. Conf.Proc. C680519: 367 s.
- ^ Gerard 't Hooft (1971). “Renormalizable Lagrangians for Massive Yang-Mills Fields”. Nuclear Physics B 35: 167. doi:10.1016/0550-3213(71)90139-8.
- ^ Gerard 't Hooft and M. J. G. Veltman (1972). “Regularization and Renormalization of Gauge Fields”. Nuclear Physics B 44: 189. doi:10.1016/0550-3213(72)90279-9.
- ^ Makoto Kobayashi and Toshihide Maskawa (1973). “CP Violation in the Renormalizable Theory of Weak Interaction”. Progress of Theoretical Physics 49: 652. doi:10.1143/PTP.49.652.
- ^ D. J. Gross and Frank Wilczek (1973). “Ultraviolet Behavior of Nonabelian Gauge Theories”. Physical Review Letters 30: 1343. doi:10.1103/PhysRevLett.30.1343.
- ^ H. David Politzer (1973). “Reliable Perturbative Results for Strong Interactions?”. Physical Review Letters 30: 1346. doi:10.1103/PhysRevLett.30.1346.
- ^ E598 Collaboration (1974). “Experimental Observation of a Heavy Particle J”. Physical Review Letters 33: 1404. doi:10.1103/PhysRevLett.33.1404.
- ^ SLAC-SP-017 Collaboration (1974). “Discovery of a Narrow Resonance in e+ e- Annihilation”. Physical Review Letters 33: 1406. doi:10.1103/PhysRevLett.33.1406.
- ^ S. W. Herb, D. C. Hom, L. M. Lederman, J. C. Sens, H. D. Snyder, J. K. Yoh, J. A. Appel, B. C. Brown, C. N. Brown, W. R. Innes, K. Ueno, T. Yamanouchi, A. S. Itoh, H. Jostlein, D. M. Kaplan and R. D. Kephart (1977). “Observation of a Dimuon Resonance at 9.5-GeV in 400-GeV Proton-Nucleus Collisions”. Physical Review Letters 39: 252. doi:10.1103/PhysRevLett.39.252.
- ^ UA1 Collaboration (1983). “Experimental Observation of Isolated Large Transverse Energy Electrons with Associated Missing Energy at s**(1/2) = 540-GeV”. Physics Letters B 122: 103. doi:10.1016/0370-2693(83)91177-2.
- ^ UA1 Collaboration (1983). “Experimental Observation of Lepton Pairs of Invariant Mass Around 95-GeV/c**2 at the CERN SPS Collider”. Physics Letters B 126: 398. doi:10.1016/0370-2693(83)90188-0.
- ^ CDF Collaboration (1995). “Observation of top quark production in ppbar collisions”. Physical Review Letters 74: 2626. doi:10.1103/PhysRevLett.74.2626.
- ^ D0 Collaboration (1995). “Observation of the top quark”. Physical Review Letters 74: 2632. doi:10.1103/PhysRevLett.74.2632.
- ^ ATLAS Collaboration (2012). “Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC”. Physics Letters B 716: 1. doi:10.1016/j.physletb.2012.08.020.
- ^ CMS Collaboration (2012). “Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC”. Physics Letters B 716: 30. doi:10.1016/j.physletb.2012.08.021.
- ^ Super-Kamiokande Collaboration (1998). “Evidence for oscillation of atmospheric neutrinos”. Physical Review Letters 81: 1562. doi:10.1103/PhysRevLett.81.1562.
- ^ Sacha Davidson, Enrico Nardi and, Yosef Nir (2008). “Leptogenesis”. Physics Report 466: 105. doi:10.1016/j.physrep.2008.06.002.
- ^ “素粒子物理学を覆すミューオンの挙動、未知の物理法則が存在か”. ナショナルジオグラフィック日本語版 (2021年4月13日). 2021年4月27日閲覧。
- ^ 素粒子「標準理論」のずれ検証に一歩 実験値を高精度測定 米研究所、(朝日新聞、2023年8月11日)
参考文献
[編集]論文
[編集]- Beringer, J.; Arguin, J.; Barnett, R.; Copic, K.; Dahl, O.; Groom, D.; Lin, C.; Lys, J. et al. (2012). “Review of Particle Physics”. Physical Review D 86 (1). doi:10.1103/PhysRevD.86.010001. ISSN 1550-7998.
書籍
[編集]- M. E. Peskin, D.V. Schroeder (1995). An Introduction to Quantum Field Theory. Westview Press. ISBN 978-0-201-50397-5
- 南部陽一郎、他『大学院素粒子物理1』講談社、1997年。ISBN 4-06-153224-3。
関連項目
[編集]外部リンク
[編集]![]() ウィキメディア・コモンズには、標準模型に関するメディアがあります。
ウィキメディア・コモンズには、標準模型に関するメディアがあります。
- 電子・陽電子リニアコライダー計画[リンク切れ]
- The Review of Particle Physics (2023) (素粒子物理学の総論) - 2022年までの素粒子の実験と理論をまとめた論文
- 素粒子の標準模型


