코쥘 접속

미분기하학에서 코쥘 접속(Koszul接續, 영어: Koszul connection)은 벡터 다발의 각 올들을 이어붙여, 벡터장의 미분을 정의할 수 있게 하는 구조이다.

매끄러운 다양체 ${\displaystyle M}$ 위의 매끄러운 벡터 다발 ${\displaystyle \pi \colon E\twoheadrightarrow M}$이 주어졌다고 하자. ${\displaystyle E}$의 매끄러운 단면들의 실수 벡터 공간을 ${\displaystyle \Gamma ^{\infty }(E)}$라고 하자.

${\displaystyle E}$ 위의 코쥘 접속은 다양하게 정의될 수 있다.

• 코쥘 접속은 벡터 다발의 매끄러운 단면 위에 작용하는 작용소로 정의될 수 있다.
• 코쥘 접속은 벡터 다발의 선형 구조와 호환되는 에레스만 접속으로 정의될 수 있다.
• 코쥘 접속은 벡터 값 미분 형식 위에 작용하는 작용소로 정의될 수 있다.

${\displaystyle M}$ 위의 아핀 접속(affine接續, 영어: affine connection)은 그 접다발 ${\displaystyle \mathrm {T} M}$ 위의 코쥘 접속이다. 아핀 접속을 갖춘 매끄러운 다양체를 아핀 다양체(affine多樣體, 영어: affine manifold)라고 한다.

${\displaystyle E}$ 위의 (코쥘) 접속 또는 공변 미분(共變微分, 영어: covariant derivative)

${\displaystyle \nabla \colon \Gamma ^{\infty }(E)\to \Gamma ^{\infty }(\mathrm {T} ^{*}M\otimes _{\mathbb {R} }E)}$

은 다음과 같은 곱 규칙을 만족시키는 실수 선형 변환이다.^{[1]:101, Definition 4.1.1}

${\displaystyle \nabla (fs)=f\nabla s+\mathrm {d} f\otimes s\qquad \forall f\in {\mathcal {C}}^{\infty }(M,\mathbb {R} ),\;s\in \Gamma ^{\infty }(E)}$

여기서 ${\displaystyle T^{*}M}$은 ${\displaystyle M}$의 공변접다발이며, ${\displaystyle \mathrm {d} f\in \Gamma ^{\infty }(\mathrm {T} ^{*}M)=\Omega ^{1}(M)}$은 ${\displaystyle f}$의 외미분으로 얻은 1차 미분 형식이다. 이는 ${\displaystyle E\to \mathrm {T} ^{*}M\otimes E}$ 1차 미분 연산자를 이룬다.

임의의 벡터장 ${\displaystyle X\in \Gamma ^{\infty }(\mathrm {T} M)}$에 대하여,

${\displaystyle \nabla _{X}\colon \Gamma ^{\infty }(E)\to \Gamma ^{\infty }(E)}$

${\displaystyle \nabla _{X}\colon s\mapsto \langle X,\nabla s\rangle }$

를 정의할 수 있다. 이를 ${\displaystyle E}$의 단면의 ${\displaystyle X}$방향의 공변 미분이라고 한다.^{[1]:101–101, (4.1.2)}

${\displaystyle \nabla }$는 1차 미분 연산자이므로, 국소 좌표계에서 다음과 같은 꼴로 전개할 수 있다.

${\displaystyle (\nabla _{X}s)^{a}=X^{i}\left(\partial _{i}s^{a}+\Gamma _{ib}^{a}s^{b}\right)}$

여기서 ${\displaystyle i,j,\dotsc }$는 접다발의 첨자이며 ${\displaystyle a,b,\dotsc }$는 ${\displaystyle E}$의 첨자이다. 코쥘 접속을 정의하는 성분 ${\displaystyle \Gamma _{ib}^{a}}$을 크리스토펠 기호라고 한다.

벡터 다발 ${\displaystyle E}$의 수직 벡터 다발은 ${\displaystyle \mathrm {V} E=E\times _{M}E}$이다. 이제, 실수 ${\displaystyle \lambda \in \mathbb {R} }$에 대한 곱셈

${\displaystyle (\cdot \lambda )\colon E\to E}$

의 미분

${\displaystyle \mathrm {T} (\cdot \lambda )\colon \mathrm {T} E\to \mathrm {T} E}$

을 생각하자. 또한, 합

${\displaystyle (+)\colon E\times E\to E}$

의 미분

${\displaystyle \mathrm {T} (+)\colon \mathrm {T} E\times \mathrm {T} E\to \mathrm {T} E}$

를 생각하자.

${\displaystyle E}$ 위의 에레스만 접속 ${\displaystyle H\subseteq \mathrm {T} E}$가 다음 조건을 만족시킨다면, 코쥘 접속이라고 한다.

${\displaystyle H_{\lambda e}=\left(\mathrm {T} (\cdot \lambda )\right)(H_{e})}$

${\displaystyle \left(\mathrm {T} (+)\right)(H\times _{M}H)=H}$

여기서 ${\displaystyle H\times _{M}H\subseteq E\times _{M}E}$이다.

에레스만 접속을 통한 정의와 단면 위의 작용을 통한 정의 사이의 관계는 다음과 같다. 우선,

${\displaystyle \operatorname {proj} _{\mathrm {V} E}\colon \mathrm {T} E\to \mathrm {V} E=\pi ^{*}E}$

가 ${\displaystyle H}$를 사용한, 수직 벡터 다발 ${\displaystyle \mathrm {V} E}$ 위로의 사영이라고 하자 (즉, ${\displaystyle H=\ker \operatorname {proj} _{\mathrm {V} E}}$). 임의의 단면 ${\displaystyle s\in \Gamma ^{\infty }(E)}$에 대하여, 미분

${\displaystyle \mathrm {T} s\colon \mathrm {T} M\to \mathrm {T} E}$

를 생각하자. 그렇다면, 다음을 정의하자.

${\displaystyle \nabla \colon \mathrm {T} M\to s^{*}\mathrm {V} E=E}$

${\displaystyle \nabla s=\operatorname {proj} _{H}\circ \mathrm {T} s}$

그렇다면, 이는 적절한 곱 규칙을 만족시켜, 후자의 정의에 해당한다.

매끄러운 다양체 ${\displaystyle M}$ 위의 매끄러운 벡터 다발 ${\displaystyle E}$ 위의 코쥘 접속

${\displaystyle \mathrm {d} ^{\nabla }\colon \Omega ^{\bullet }(M;E)\to \Omega ^{\bullet +1}(M;E)}$

은 다음과 같은 곱 규칙을 만족시키는 실수 선형 변환이다.

${\displaystyle \mathrm {d} ^{\nabla }(\alpha \wedge \omega )=\mathrm {d} \alpha \wedge \omega +(-)^{p}\alpha \wedge \mathrm {d} ^{\nabla }\omega \qquad \forall \alpha \in \Omega ^{p}(M),\;\omega \in \Omega (M;E)}$

(여기서 ${\displaystyle \Omega (M;E)}$는 ${\displaystyle E}$값 미분 형식의 공간이다.) 이러한 연산자를 공변 외미분(共變外微分, 영어: covariant exterior derivative)이라고 한다.

단면 위의 작용을 통한 정의와 미분 형식 위의 작용을 통한 정의 사이의 관계는 다음과 같다. 임의의 공변 외미분 ${\displaystyle \mathrm {d} ^{\nabla }\colon \Omega ^{\bullet }(M;E)\to \Omega ^{\bullet +1}(M;E)}$가 주어졌을 때,

${\displaystyle \Omega ^{0}(M;E)=\Gamma ^{\infty }(E)}$

이므로,

${\displaystyle \mathrm {d} ^{\nabla }|_{\Gamma ^{\infty }(E)}\colon \Gamma ^{\infty }(M;E)\to \Omega ^{1}(M;E)=\Gamma ^{\infty }(\mathrm {T} ^{*}M\otimes _{\mathbb {R} }E)}$

는 단면 위에 적절한 곱 규칙을 만족시킨다. 반대로, 단면 위의 작용소 ${\displaystyle \nabla \colon \Gamma ^{\infty }(E)\to \Gamma ^{\infty }(\mathrm {T} ^{*}M\otimes _{\mathbb {R} }E)}$가 주어졌을 때, 미분 형식에 대한 곱 규칙을 만족시키게 유일하게 확장할 수 있다.

일반적 외미분과 달리, 공변 외미분은 일반적으로 ${\displaystyle \mathrm {d} ^{\nabla }\circ \mathrm {d} ^{\nabla }=0}$을 만족시키지 못한다.

코쥘 접속의 개념을 ${\displaystyle \mathbb {Z} /2}$-등급 벡터 공간(초벡터 공간)에 대하여 일반화하여, 코쥘 초접속(Koszul初接續, 영어: Koszul superconnection)의 개념을 정의할 수 있다.^{[2]:44, §1.4}

구체적으로, 다음 데이터가 주어졌다고 하자.

• 매끄러운 다양체 ${\displaystyle M}$
• 두 매끄러운 벡터 다발 ${\displaystyle E^{\pm }\twoheadrightarrow M}$. ${\displaystyle E=E^{+}\oplus E^{-}}$라고 표기하자.

그렇다면, ${\displaystyle E}$ 위의 코쥘 초접속은 다음 조건을 만족시키는 선형 변환

${\displaystyle \nabla ^{\pm }\colon \Gamma ^{\infty }(E^{\pm })\to \bigoplus _{n=0}^{\infty }\Omega ^{2n}(M;E^{\mp })\oplus \bigoplus _{n=0}^{\infty }\Omega ^{2n+1}(M;E^{\pm })}$

이다.

${\displaystyle \nabla ^{\pm }(fs)=f\nabla s+(\mathrm {d} f)\otimes s\qquad \forall f\in {\mathcal {C}}^{\infty }(M;\mathbb {R} ),\;s\in \Gamma ^{\infty }(E^{\pm })}$

공변 외미분을 통한 정의 역시 코쥘 초접속에 대하여 적용할 수 있다.

구체적으로, 다음 데이터가 주어졌다고 하자.

• 매끄러운 다양체 ${\displaystyle M}$
• 두 매끄러운 벡터 다발 ${\displaystyle E^{\pm }\twoheadrightarrow M}$. ${\displaystyle E=E^{+}\oplus E^{-}}$라고 표기하자.

그렇다면, 다음을 정의할 수 있다. ${\displaystyle E^{\pm }}$값 미분 형식들의 공간 ${\displaystyle \Omega ^{\bullet }(M;E^{\pm })}$으로부터,

${\displaystyle \Omega ^{\pm ,k}(M;E)={\begin{cases}\Omega ^{k}(M;E^{\pm })&k\mid 2\\\Omega ^{k}(M;E^{\mp })&k\nmid 2\end{cases}}}$

${\displaystyle \Omega ^{\pm }(M;E)=\bigoplus _{k\in \mathbb {N} }\Omega ^{\pm ,k}(M;E)}$

즉, 아래 표에서, 흰색 바탕은 ${\displaystyle \Omega ^{+}(M;E)}$에, 회색 바탕은 ${\displaystyle \Omega ^{-}(M;E)}$에 속한다.

${\displaystyle \Omega ^{0}(M;E^{+})=\Gamma ^{\infty }(E^{+})}$	${\displaystyle \Omega ^{1}(M;E^{+})}$	${\displaystyle \Omega ^{2}(M;E^{+})}$	${\displaystyle \Omega ^{3}(M;E^{+})}$	${\displaystyle \Omega ^{4}(M;E^{+})}$
${\displaystyle \Omega ^{0}(M;E^{-})=\Gamma ^{\infty }(E^{-})}$	${\displaystyle \Omega ^{1}(M;E^{-})}$	${\displaystyle \Omega ^{2}(M;E^{-})}$	${\displaystyle \Omega ^{3}(M;E^{-})}$	${\displaystyle \Omega ^{4}(M;E^{-})}$

그렇다면, ${\displaystyle E^{\pm }}$ 위의 코쥘 초접속

${\displaystyle \mathrm {d} ^{\nabla }\colon \Omega ^{\pm }(M;E)\to \Omega ^{\mp }(M;E)}$

은 다음과 같은 곱 규칙을 만족시키는 실수 선형 변환이다.^{[2]:44, Definition 1.37}

${\displaystyle \mathrm {d} ^{\nabla }(\alpha \wedge \omega )=(\mathrm {d} \alpha )\wedge \omega +(-)^{p}\alpha \wedge \mathrm {d} ^{\nabla }\theta \qquad \forall \alpha \in \Omega ^{p}(M),\;\omega \in \Omega (M;E)}$

매우 구체적으로, 매끄러운 다양체 ${\displaystyle M}$ 위의 두 매끄러운 벡터 다발 ${\displaystyle E^{\pm }\twoheadrightarrow M}$ 위의 코쥘 초접속은 다음과 같은 데이터로 주어진다.^{[2]:45, Proposition 1.39}

• ${\displaystyle E^{\pm }}$ 위의 코쥘 접속 ${\displaystyle \nabla _{E^{\pm }}}$. 이는 코쥘 초접속의 1등급 성분이다.
• 음이 아닌 짝수 ${\displaystyle i\in 2\mathbb {N} =\{0,2,4,\dotsc \}}$에 대하여, 벡터 값 미분 형식 ${\displaystyle T^{i}\in \Omega ^{i}(M;E^{+}\otimes (E^{-})^{*}\oplus E^{-}\otimes (E^{+})^{*})}$
• 3 이상의 홀수 ${\displaystyle i\in \{3,5,7,\dotsc \}}$에 대하여, 벡터 값 미분 형식 ${\displaystyle T^{i}\in \Omega ^{i}(M;E^{+}\otimes (E^{+})^{*}\oplus E^{-}\otimes (E^{-})^{*})}$

이 데이터는 ${\displaystyle \Gamma ^{\infty }(M;E^{\pm })}$ 위에 다음과 같이 작용한다.

${\displaystyle \mathrm {d} ^{\nabla }(\alpha \otimes s^{\pm })=\nabla _{E^{\pm }}s^{\pm }\wedge \alpha +\sum _{i\in \mathbb {N} \setminus \{1\}}T^{i}(s)\qquad \forall s^{\pm }\in \Gamma ^{\infty }(E^{\pm })}$

이 데이터는 ${\displaystyle \Omega (M;E)}$ 위에 다음과 같이 작용한다.

${\displaystyle \mathrm {d} ^{\nabla }(\alpha \otimes s^{\pm })=\nabla _{E^{\pm }}s^{\pm }\wedge \alpha +\sum _{i\in \mathbb {N} \setminus \{1\}}T^{i}(s)\wedge \alpha \qquad \forall s^{\pm }\in \Gamma ^{\infty }(E^{\pm }),\;\alpha \in \Omega ^{p}(M)}$

이러한 성분들은 초접속의 "크리스토펠 기호"에 해당한다.

다음과 같은 데이터가 주어졌다고 하자.

• 두 매끄러운 다양체 ${\displaystyle M}$, ${\displaystyle N}$
• 그 사이의 매끄러운 함수 ${\displaystyle f\colon M\to N}$
• ${\displaystyle N}$ 위의 매끄러운 벡터 다발 ${\displaystyle E\twoheadrightarrow N}$
• ${\displaystyle E}$ 위의 코쥘 접속 ${\displaystyle \nabla }$

그렇다면, ${\displaystyle f}$를 통해 ${\displaystyle M}$위의 당김 다발 ${\displaystyle f^{*}E}$를 정의할 수 있다. 이 위에 당김 접속

${\displaystyle f^{*}\nabla \colon \Gamma ^{\infty }(f^{*}E)\to \Gamma ^{\infty }(T^{*}M\otimes f^{*}E)}$

은 다음 조건을 만족시키는 유일한 코쥘 접속이다.

${\displaystyle f^{*}\nabla _{X}\colon f^{*}s\mapsto f^{*}(\nabla _{f_{*}X}s)\qquad \forall s\in \Gamma ^{\infty }(E),\;X\in \Gamma ^{\infty }(TM)}$

여기서 ${\displaystyle f_{*}X=df(X)\in \Gamma ^{\infty }(\mathrm {T} N)}$는 ${\displaystyle X\in \Gamma ^{\infty }(\mathrm {T} M)}$의 ${\displaystyle N}$으로의 밂(영어: pushforward)이다.

마찬가지로, 만약 ${\displaystyle N}$ 위에 두 매끄러운 벡터 다발 ${\displaystyle E^{\pm }\twoheadrightarrow N}$이 주어졌을 때, ${\displaystyle E^{\pm }}$ 위의 코쥘 초접속을 당김 다발 ${\displaystyle f^{*}E^{\pm }}$ 위로 당길 수 있다.

매끄러운 벡터 다발 ${\displaystyle E\twoheadrightarrow M}$ 위의 코쥘 접속 ${\displaystyle \nabla }$에 대하여, 다음 조건을 만족시키는 텐서장 ${\displaystyle F^{\nabla }\in \Omega ^{2}(M;\operatorname {End} E)}$가 유일하게 존재한다.

${\displaystyle F^{\nabla }(X,Y)\colon s\mapsto \nabla _{X}\nabla _{Y}s-\nabla _{Y}\nabla _{X}s-\nabla _{[X,Y]}s\qquad \forall X,Y\in \Gamma ^{\infty }(\mathrm {T} M),\;s\in \Gamma ^{\infty }(E)}$

이를 ${\displaystyle \nabla }$의 곡률(曲率, 영어: curvature)이라고 하며, 이는 ${\displaystyle \operatorname {End} E\cong E\otimes E^{*}}$값의 2차 미분 형식이다.^{[1]:108–109, §4.1} 여기서 ${\displaystyle [X,Y]}$는 벡터장의 리 미분이다. 이는 일반적 올다발 위의 에레스만 접속의 곡률의 특수한 경우이다.

곡률이 0인 코쥘 접속을 평탄 코쥘 접속(平坦Koszul接續, 영어: flat Koszul connection)이라고 한다.

아핀 접속의 곡률은 리만 곡률이라고 하며, 이는 (3,1)-텐서장으로 여길 수 있다. 또한, 아핀 접속 ${\displaystyle \nabla }$의 경우, 곡률과 더불어 비틀림을 정의할 수 있다. 비틀림 ${\displaystyle T^{\nabla }\in \Omega ^{2}(M;\mathrm {T} M)}$은 다음과 같다.

${\displaystyle T^{\nabla }(X,Y)=\nabla _{X}Y-\nabla _{Y}X-[X,Y]}$

(여기서 ${\displaystyle \Omega ^{2}(M;\mathrm {T} M)}$은 접다발 값 2차 미분 형식의 공간이다.) 비틀림은 (2,1)-텐서장으로 여길 수 있다.

마찬가지로, 매끄러운 다양체 ${\displaystyle M}$ 위의 두 매끄러운 벡터 다발 ${\displaystyle E^{\pm }}$ 위의 코쥘 초접속 ${\displaystyle \nabla }$가 주어졌을 때,

${\displaystyle \mathrm {d} ^{\nabla }\circ \mathrm {d} ^{\nabla }\colon \Omega ^{\pm }(M;E)\to \Omega ^{\pm }(M;E)}$

는 항상 다음과 같은 꼴이다.^{[2]:44, Proposition 1.38}

${\displaystyle \mathrm {d} ^{\nabla }\circ \mathrm {d} ^{\nabla }\in \Omega (M;\operatorname {End} (E))}$

이를 초접속의 곡률이라고 한다.^{[2]:44, §1.4} 곡률이 0인 코쥘 초접속을 평탄 코쥘 초접속(平坦Koszul超接續,영어: flat Koszul superconnection)이라고 한다.

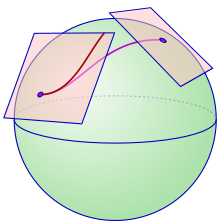
코쥘 접속은 에레스만 접속의 특수한 경우이므로, 평행 운송(영어: parallel transport)을 정의할 수 있다. 구체적으로, 다음과 같은 데이터가 주어졌다고 하자.

• 매끄러운 벡터 다발 ${\displaystyle E\twoheadrightarrow M}$
• ${\displaystyle E}$의 매끄러운 단면 ${\displaystyle s\in \Gamma ^{\infty }(E)}$
• ${\displaystyle E}$ 위의 코쥘 접속 ${\displaystyle \nabla }$
• 매끄러운 곡선 ${\displaystyle \gamma \colon [0,1]\to M}$

만약

${\displaystyle \nabla _{{\dot {\gamma }}(t)}\sigma =0\qquad \forall t\in [0,1]}$

이 성립한다면, ${\displaystyle E}$를 평행 단면(平行斷面, 영어: parallel section)이라고 한다. 이는 단면의 당김 ${\displaystyle \gamma ^{*}s\in \Gamma ^{\infty }(\gamma ^{*}E)}$의, 당겨진 접속 ${\displaystyle \gamma ^{*}\nabla }$에 대한 공변 미분이 0이라는 것과 동치이다.

이 경우, ${\displaystyle s(\gamma (1))\in E_{\gamma (1)}}$를 ${\displaystyle s(\gamma (0))\in E_{\gamma (0)}}$의, 곡선 ${\displaystyle \gamma }$를 따른 평행 운송이라고 한다. 평행 운송은 선형 변환

${\displaystyle \tau _{\gamma }\colon E_{\gamma (0)}\to E_{\gamma (1)}}$

으로 생각할 수 있으며, 이는 벡터 공간의 동형을 이룬다. 이와 같이, 코쥘 접속은 ${\displaystyle E}$의 각 올공간들을 (주어진 경로에 따라) "이어붙이는" 것을 알 수 있다.

마찬가지로, 코쥘 초접속 역시 일종의 평행 운송을 정의한다.^[3]

공변 미분 ${\displaystyle \nabla s}$의, ${\displaystyle x\in M}$에서의 값은 ${\displaystyle s}$의 ${\displaystyle x}$ 근방의 값에만 의존한다.^{[1]:102, Remark 2}

매끄러운 벡터 다발 ${\displaystyle E\twoheadrightarrow M}$ 위의 두 코쥘 접속 ${\displaystyle \nabla ^{1}}$, ${\displaystyle \nabla ^{2}}$이 주어졌다고 하자. 그렇다면,

${\displaystyle \nabla ^{1}-\nabla ^{2}\colon \Gamma ^{\infty }(E)\to \Gamma ^{\infty }(T^{*}M\otimes E)}$

는 매끄러운 다발 사상을 이룬다. 즉, ${\displaystyle (\nabla ^{1}-\nabla ^{2})(s)}$의 ${\displaystyle x\in M}$에서의 값은 ${\displaystyle s(x)\in E_{x}M}$에만 의존한다.

${\displaystyle \nabla ^{1}-\nabla ^{2}\in =\Omega ^{1}\left(M;\operatorname {End} (E)\right)=\Omega ^{1}(M;E\otimes E^{*})}$

이에 따라, ${\displaystyle E}$ 위의 코쥘 접속들의 모듈라이 공간은 ${\displaystyle \Omega ^{1}(M;\operatorname {End} (E))}$의 꼴의 아핀 공간이다.

마찬가지로, 두 매끄러운 벡터 다발 ${\displaystyle E^{\pm }\twoheadrightarrow M}$ 위의 두 코쥘 초접속 ${\displaystyle \nabla ^{1}}$, ${\displaystyle \nabla ^{2}}$이 주어졌을 때,

${\displaystyle \nabla ^{1}-\nabla ^{2}\in \Omega ^{-}(M;\operatorname {End} (E))=\bigoplus _{i=0}^{\infty }\Omega ^{2i}\left(M;E^{+}\otimes (E^{-})^{*}\oplus E^{-}\otimes (E^{+})^{*}\right)\oplus \bigoplus _{i=0}^{\infty }\Omega ^{2i+1}\left(M;E^{+}\otimes (E^{+})^{*}\oplus E^{-}\otimes (E^{-})^{*}\right)}$

이며, ${\displaystyle E}$ 위의 코쥘 초접속들의 모듈라이 공간은 ${\displaystyle \Omega ^{-}(M;\operatorname {End} (E))}$의 꼴의 아핀 공간이다.^{[2]:45, Corollary 1.40}

매끄러운 다양체 ${\displaystyle M}$ 위에 자명한 벡터 다발 ${\displaystyle E=M\times \mathbb {R} ^{k}\twoheadrightarrow M}$이 주어졌다고 하자. ${\displaystyle \mathbb {R} ^{k}}$의 기저를 ${\displaystyle \{e_{1},\dots ,e_{k}\}}$라고 하자. 그렇다면, ${\displaystyle E}$의 단면은 매끄러운 함수로 생각할 수 있다.

${\displaystyle \Gamma ^{\infty }(E)\cong {\mathcal {C}}^{\infty }(M,\mathbb {R} ^{n})}$

이 경우, ${\displaystyle E}$ 위의 모든 코쥘 접속은 다음과 같은 꼴이다.

${\displaystyle \nabla \colon s\mapsto ds+\omega (s)}$

여기서

${\displaystyle \omega \in \Omega ^{1}(M)\otimes _{\mathbb {R} }\operatorname {End} (\mathbb {R} ^{n})}$

는 1차 미분 형식의 ${\displaystyle n\times n}$ 정사각 행렬이며,

${\displaystyle ds=\sum _{i}e_{i}d\langle e_{i},s_{i}\rangle \in \Gamma ^{\infty }(\mathrm {T} ^{*}\!M\otimes E)}$

는 ${\displaystyle s\colon M\to \mathbb {R} ^{n}}$의 각 벡터 성분에 대한 외미분이다. 이 경우,

${\displaystyle (\omega )^{i}{}_{j}=\langle e_{j},\nabla e_{j}\rangle }$

를 ${\displaystyle \nabla }$의 접속 형식(接續形式, 영어: connection form)이라고 한다. 만약 접속 형식이 0이라면, 코쥘 접속은 평탄 코쥘 접속을 이룬다.

보다 일반적으로, 임의의 벡터 다발의 경우 국소적 자명화를 (비표준적으로) 잡을 수 있으며, 위와 같이 접속 형식을 정의할 수 있다. 물론 이는 선택한 국소적 자명화에 의존하며, 또 일반적으로 대역적으로 정의될 수 없다.

 이 부분의 본문은 레비치비타 접속입니다.

준 리만 다양체 ${\displaystyle (M,g)}$ 위에는 리만 계량으로부터 레비치비타 접속이라는 아핀 접속을 표준적으로 정의할 수 있다.

 이 부분의 본문은 스핀 접속입니다.

리만 계량을 갖춘 스핀 다양체 ${\displaystyle (M,g)}$ 위의 스피너 다발 ${\displaystyle \mathrm {S} M}$ 위에, 리만 계량으로 유도되는 표준적인 코쥘 (초)접속인 스핀 접속이 존재한다.

아핀 접속의 개념은 19세기의 기하학 및 텐서 미적분학 등에서 유래하였다. 1920년대 초에 엘리 카르탕은 카르탕 접속 이론의 일부로서 아핀 접속의 개념을 체계적으로 개발하였고, 이와 동시에 헤르만 바일은 일반 상대성 이론의 수학적 기초를 위하여 접속 이론을 개발하였다. "접속"이라는 용어 역시 카르탕이 도입하였다.

1950년에 장루이 코쥘은 접다발 위의 아핀 접속의 개념을 일반화하여, 임의의 벡터 다발 위의 코쥘 접속의 현대적인 정의를 제시하였다.^[4]

초접속의 개념은 1985년에 대니얼 퀼런이 천 특성류를 연구하기 위해 도입하였다.^{[5]:90, §2}

• D가군

• “Affine connection”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4. 
• “Linear connection”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4. 
• Weisstein, Eric Wolfgang. “Vector bundle connection”. 《Wolfram MathWorld》 (영어). Wolfram Research. 
• “Affine connection”. 《nLab》 (영어). 
• “Connection on a vector bundle”. 《nLab》 (영어). 
• “Superconnection”. 《nLab》 (영어). 
• 이철희. “접속 (connection)”. 《수학노트》.