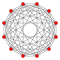
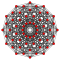
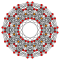
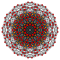
Cantellated 6-orthoplexes

6-orthoplex				Cantellated 6-orthoplex				Bicantellated 6-orthoplex
6-cube				Cantellated 6-cube				Bicantellated 6-cube
Cantitruncated 6-orthoplex			Bicantitruncated 6-orthoplex			Bicantitruncated 6-cube			Cantitruncated 6-cube
Orthogonal projections in B6 Coxeter plane

In six-dimensional geometry, a cantellated 6-orthoplex is a convex uniform 6-polytope, being a cantellation of the regular 6-orthoplex.

There are 8 cantellation for the 6-orthoplex including truncations. Half of them are more easily constructed from the dual 5-cube

Cantellated 6-orthoplex
Type	uniform 6-polytope
Schläfli symbol	t0,2{3,3,3,3,4} rr{3,3,3,3,4}
Coxeter-Dynkin diagrams	=
5-faces	136
4-faces	1656
Cells	5040
Faces	6400
Edges	3360
Vertices	480
Vertex figure
Coxeter groups	B6, [3,3,3,3,4] D6, [33,1,1]
Properties	convex

• Cantellated hexacross
• Small rhombated hexacontatetrapeton (acronym: srog) (Jonathan Bowers)^[1]

There are two Coxeter groups associated with the cantellated 6-orthoplex, one with the B₆ or [4,3,3,3,3] Coxeter group, and a lower symmetry with the D₆ or [3^3,1,1] Coxeter group.

Cartesian coordinates for the 480 vertices of a cantellated 6-orthoplex, centered at the origin, are all the sign and coordinate permutations of

(2,1,1,0,0,0)

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Bicantellated 6-orthoplex
Type	uniform 6-polytope
Schläfli symbol	t1,3{3,3,3,3,4} 2rr{3,3,3,3,4}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges	8640
Vertices	1440
Vertex figure
Coxeter groups	B6, [3,3,3,3,4] D6, [33,1,1]
Properties	convex

• Bicantellated hexacross, bicantellated hexacontatetrapeton
• Small birhombated hexacontatetrapeton (acronym: siborg) (Jonathan Bowers)^[2]

There are two Coxeter groups associated with the bicantellated 6-orthoplex, one with the B₆ or [4,3,3,3,3] Coxeter group, and a lower symmetry with the D₆ or [3^3,1,1] Coxeter group.

Cartesian coordinates for the 1440 vertices of a bicantellated 6-orthoplex, centered at the origin, are all the sign and coordinate permutations of

(2,2,1,1,0,0)

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Cantitruncated 6-orthoplex
Type	uniform 6-polytope
Schläfli symbol	t0,1,2{3,3,3,3,4} tr{3,3,3,3,4}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges	3840
Vertices	960
Vertex figure
Coxeter groups	B6, [3,3,3,3,4] D6, [33,1,1]
Properties	convex

• Cantitruncated hexacross, cantitruncated hexacontatetrapeton
• Great rhombihexacontatetrapeton (acronym: grog) (Jonathan Bowers)^[3]

There are two Coxeter groups associated with the cantitruncated 6-orthoplex, one with the B₆ or [4,3,3,3,3] Coxeter group, and a lower symmetry with the D₆ or [3^3,1,1] Coxeter group.

Cartesian coordinates for the 960 vertices of a cantitruncated 6-orthoplex, centered at the origin, are all the sign and coordinate permutations of

(3,2,1,0,0,0)

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Bicantitruncated 6-orthoplex
Type	uniform 6-polytope
Schläfli symbol	t1,2,3{3,3,3,3,4} 2tr{3,3,3,3,4}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges	10080
Vertices	2880
Vertex figure
Coxeter groups	B6, [3,3,3,3,4] D6, [33,1,1]
Properties	convex

• Bicantitruncated hexacross, bicantitruncated hexacontatetrapeton
• Great birhombihexacontatetrapeton (acronym: gaborg) (Jonathan Bowers)^[4]

There are two Coxeter groups associated with the bicantitruncated 6-orthoplex, one with the B₆ or [4,3,3,3,3] Coxeter group, and a lower symmetry with the D₆ or [3^3,1,1] Coxeter group.

Cartesian coordinates for the 2880 vertices of a bicantitruncated 6-orthoplex, centered at the origin, are all the sign and coordinate permutations of

(3,3,2,1,0,0)

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

These polytopes are part of a set of 63 uniform 6-polytopes generated from the B₆ Coxeter plane, including the regular 6-cube or 6-orthoplex.

B6 polytopes
β6	t1β6	t2β6	t2γ6	t1γ6	γ6	t0,1β6	t0,2β6
t1,2β6	t0,3β6	t1,3β6	t2,3γ6	t0,4β6	t1,4γ6	t1,3γ6	t1,2γ6
t0,5γ6	t0,4γ6	t0,3γ6	t0,2γ6	t0,1γ6	t0,1,2β6	t0,1,3β6	t0,2,3β6
t1,2,3β6	t0,1,4β6	t0,2,4β6	t1,2,4β6	t0,3,4β6	t1,2,4γ6	t1,2,3γ6	t0,1,5β6
t0,2,5β6	t0,3,4γ6	t0,2,5γ6	t0,2,4γ6	t0,2,3γ6	t0,1,5γ6	t0,1,4γ6	t0,1,3γ6
t0,1,2γ6	t0,1,2,3β6	t0,1,2,4β6	t0,1,3,4β6	t0,2,3,4β6	t1,2,3,4γ6	t0,1,2,5β6	t0,1,3,5β6
t0,2,3,5γ6	t0,2,3,4γ6	t0,1,4,5γ6	t0,1,3,5γ6	t0,1,3,4γ6	t0,1,2,5γ6	t0,1,2,4γ6	t0,1,2,3γ6
t0,1,2,3,4β6	t0,1,2,3,5β6	t0,1,2,4,5β6	t0,1,2,4,5γ6	t0,1,2,3,5γ6	t0,1,2,3,4γ6	t0,1,2,3,4,5γ6

• H.S.M. Coxeter:
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
• Klitzing, Richard. "6D uniform polytopes (polypeta)". x3o3x3o3o4o - srog, o3x3o3x3o4o - siborg, x3x3x3o3o4o - grog, o3x3x3x3o4o - gaborg

• Polytopes of Various Dimensions
• Multi-dimensional Glossary