Конхоида
 Из Википедии, бесплатной энциклопедии
Из Википедии, бесплатной энциклопедии

Конхо́ида криво́й (англ. conchoid; conchoidal curve, от др.-греч. κονχοειδής — похожий на раковину) — плоская кривая, геометрическое место преобразованных концов — конхоид — радиус-векторов каждой точки исходной плоской кривой, причём эти радиус-векторы увеличены (одна ветвь конхоиды) или уменьшены (другая ветвь конхоиды) на постоянную величину . Если уравнение исходной кривой в полярной системе координат , то уравнение её конхоиды [1][2][3][4].
Начало радиус-вектора называется полюсом конхоиды (в данном случае это начало координат ), а постоянная величина приращения радим-вектора — модулем конхоиды[4].
Для получения новых плоских кривых — конхоид из старых — директрис[5], или базисов[6], используется конхоидное преобразование, при этом уравнение конхоиды могут записать в виде
Говорят о двух ветвях конхоиды, соответствующих[7][8]:
- либо прибавлению и вычитанию — положительной константы:
- либо прибавлению этой константы в противоположных направлениях.
Конхоидальный циркуль
[править | править код]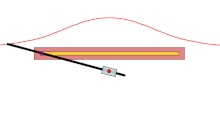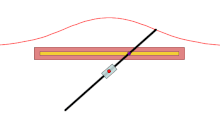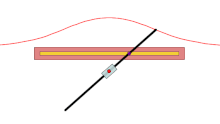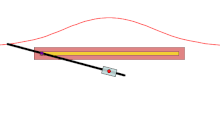
Для вычерчивания конхоиды Никомеда служит прибор конхоидограф, или конхоидальный циркуль[9].
Конхоидальные циркули бывают разных конструкций. Опишем устройство конхоидографа, показанного на рисунке справа. Основанием конхоидального циркуля служит прямоугольный планшет. Горизонтально посередине планшета укреплена вытянутая рамка, которая служит директрисой коноиды Никомеда — прямой. В середине этой рамки находится муфта, свободно движущаяся вдоль рамки и снабжённая стерженьком. Под серединой рамки на другом стерженьке закреплена другая муфта, в которую вставлена рейка. Поэтому рейка может вращаться вокруг стерженька своей муфты и двигаться вдоль этой муфты. На другом конце рейки закреплено чертящее остриё, а на расстоянии от этого конца — шайбочка, при помощи которой рейка надевается на стерженёк муфты рамки. При вращении рейки и движении её вдоль второй муфты чертящее остриё нарисует верхнюю вервь конхоиды Никомеда[9].
Примеры
[править | править код]- Конхоида прямой — конхоида Никомеда[1][2].
- Конхоида окружности — конхоида окружности[10].
- Конхоида окружности с полюсом на окружности — улитка Паскаля[1][2].
- Конхоида спирали Ферма — параболическая спираль[2][11].
- Конхоида розы — двойная линия[12].
- Конхоида архимедовой спирали — неоида[13].
- Конхоида гиперболической спирали — конхоида гиперболической спирали[14].
- Конхоида строфоиды с полюсом на вершине петли — строфоида[4].
- Конхоида Архимедовой спирали с полюсом в её центре — Архимедова спираль, изометрическая исходной[4].
- Конхоида коники с полюсом в фокусе — кривая Ержабека[4].
Примечания
[править | править код]- ↑ 1 2 3 Соколов Д. Д. Конхоида кривой, 1979.
- ↑ 1 2 3 4 Конхоида кривой, 1988.
- ↑ Конхоида, 1973.
- ↑ 1 2 3 4 5 Ferréol Robert. Conchoid, 2017.
- ↑ Zwikker C. The Advanced Geometry of Plane Curves and Their Applications, 1963, XI. Pedals and other derived curves. 3. Limacon, conchoid, с. 154.
- ↑ Савелов А. А. Плоские кривые, 1960, § 1. Конхоида Никомеда, с. 104.
- ↑ Zwikker C. The Advanced Geometry of Plane Curves and Their Applications, 1963, XI. Pedals and other derived curves. 3. Limacon, conchoid, с. 154; 287.
- ↑ Савелов А. А. Плоские кривые, 1960, § 1. Конхоида Никомеда, с. 100.
- ↑ 1 2 Савелов А. А. Плоские кривые, 1960, § 1. Конхоида Никомеда, с. 103.
- ↑ jan wassenaar conchoid, 2013.
- ↑ Савелов А. А. Плоские кривые, 1960, § 3. Алгебраические спирали, с. 201.
- ↑ Савелов А. А. Плоские кривые, 1960, § 15. Овалы Мюнгера, с. 179.
- ↑ Савелов А. А. Плоские кривые, 1960, § 2. Спираль Архимеда, с. 194.
- ↑ Савелов А. А. Плоские кривые, 1960, § 3. Алгебраические спирали, с. 198.
Источники
[править | править код]- Конхоида // Большая советская энциклопедия. (В 30 томах) Гл. ред. А. М. Прохоров. Изд. 3-е. М.: «Советская энциклопедия», 1973. Т. 13. Конда — Кун. 1973. 608 с. с илл., 21 л. илл., 6 л. карт. С. 88.
- Конхоида кривой // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 292.
- Савелов А. А. Плоские кривые. Систематика, свойства, применения. (Справочное руководство) / Под ред. А. П. Нордена. М.: Физматлит, 1960. 293 с., ил.
- Соколов Д. Д. Конхоида кривой // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д—Коо. М.: «Советская Энциклопедия», 1979. 1104 стб., ил. Стб. 1101.
- Ferréol Robert. Conchoid // ENCYCLOPÉDIE DES FORMES MATHÉMATIQUES REMARQUABLES Архивная копия от 6 марта 2023 на Wayback Machine
- jan wassenaar conchoid // mathematical curves Архивная копия от 4 октября 2023 на Wayback Machine
- Zwikker C.[англ.] The Advanced Geometry of Plane Curves and Their Applications[англ.]The Advanced Geometry of Plane Curves and Their Applications. New York: Dover Publications, Inc., 1963. 299 p. ISBN 0486610780. ISBN 9780486610788.







