Оригинальная тета-функция Якоби θ 1 {\displaystyle \theta _{1}} u = i π z {\displaystyle u=i{\pi }z} номом [en] q = e i π τ = 0 , 1 e 0 , 1 i π {\displaystyle q=e^{i{\pi }\tau }=0,1e^{0,1i\pi }} θ 1 ( u ; q ) = 2 q 1 4 ∑ n = 0 ∞ ( − 1 ) n q n ( n + 1 ) sin ( 2 n + 1 ) u = ∑ n = − ∞ n = ∞ ( − 1 ) n − 1 2 q ( n + 1 2 ) 2 e ( 2 n + 1 ) i u {\displaystyle {\begin{aligned}\theta _{1}(u;q)&=2q^{\frac {1}{4}}\sum _{n=0}^{\infty }(-1)^{n}q^{n(n+1)}\sin(2n+1)u\\&=\sum _{n=-\infty }^{n=\infty }(-1)^{n-{\frac {1}{2}}}q^{\left(n+{\frac {1}{2}}\right)^{2}}e^{(2n+1)iu}\end{aligned}}} Тета-функции — это специальные функции от нескольких комплексных переменных . Они играют важную роль во многих областях, включая теории абелевых многообразий , пространства модулей и квадратичных форм . Они применяются также в теории солитонов . После обобщения к алгебре Грассмана функции появляются также в квантовой теории поля [1]
Наиболее распространённый вид тета-функций — это функции, встречающиеся в теории эллиптических функций . По отношению к одной из комплексных переменных (обычно обозначаемой z ) тета-функция имеет свойство, выражающееся в сложении периодов ассоциированных эллиптических функций, что делает их квазипериодическими [en] линейного расслоения [en] понижения [en]
Тета-функция 1 Якоби Тета-функция 2 Якоби Тета-функция 3 Якоби Тета-функция 4 Якоби Имеется несколько связанных функций, которые называются тета-функциями Якоби, и много различных и несовместимых систем их обозначения. Одна тета-функция Якоби (названа именем Карла Густава Якоби ), это функция, определённая от двух комплексных переменных z и τ {\displaystyle \tau } z может быть любым комплексным числом , а τ {\displaystyle \tau } верхней половиной плоскости , что означает, что число имеет положительную мнимую часть. Функция задаётся формулой
ϑ ( z ; τ ) = ∑ n = − ∞ ∞ exp ( π i n 2 τ + 2 π i n z ) = = 1 + 2 ∑ n = 1 ∞ ( e π i τ ) n 2 cos ( 2 π n z ) = ∑ n = − ∞ ∞ q n 2 η n , {\displaystyle {\begin{aligned}\vartheta (z;\tau )&=\sum _{n=-\infty }^{\infty }\exp \left(\pi in^{2}\tau +2\pi inz\right)=\\&=1+2\sum _{n=1}^{\infty }\left(e^{\pi i\tau }\right)^{n^{2}}\cos(2\pi nz)=\sum _{n=-\infty }^{\infty }q^{n^{2}}\eta ^{n},\end{aligned}}} где q = exp ( π i τ ) {\displaystyle q=\exp(\pi {i}\tau )} η = exp ( 2 π i z ) {\displaystyle \eta =\exp(2\pi {i}z)} формой Якоби [en] τ {\displaystyle \tau } рядом Фурье для периодической целой функции от z с периодом 1. В этом случае тета-функция удовлетворяет тождеству
ϑ ( z + 1 ; τ ) = ϑ ( z ; τ ) . {\displaystyle \vartheta (z+1;\tau )=\vartheta (z;\tau ).} Функция ведёт себя очень регулярно с учётом квазипериода τ {\displaystyle \tau }
ϑ ( z + a + b τ ; τ ) = exp ( − π i b 2 τ − 2 π i b z ) ϑ ( z ; τ ) , {\displaystyle \vartheta (z+a+b\tau ;\tau )=\exp \left(-\pi ib^{2}\tau -2\pi ibz\right)\,\vartheta (z;\tau ),} где a и b — целые числа.
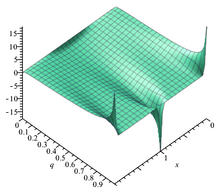
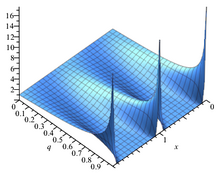
Тета-функция θ 1 {\displaystyle \theta _{1}} номами [en] q = e i π τ {\displaystyle q=e^{i{\pi }\tau }} q при изменении τ {\displaystyle \tau } Тета-функция θ 1 {\displaystyle \theta _{1}} номами [en] q = e i π τ {\displaystyle q=e^{i{\pi }\tau }} q при изменении τ {\displaystyle \tau } Тета-функция Якоби, определённая выше, иногда рассматривается вместе с тремя дополнительными тета-функциями и в этом случае записывается с дополнительным индексом 0:
ϑ 00 ( z ; τ ) = ϑ ( z ; τ ) {\displaystyle \vartheta _{00}(z;\tau )=\vartheta (z;\tau )} Дополнительные (полупериодичные) функции определяются формулами
ϑ 01 ( z ; τ ) = ϑ ( z + 1 2 ; τ ) ϑ 10 ( z ; τ ) = exp ( 1 4 π i τ + π i z ) ϑ ( z + 1 2 τ ; τ ) ϑ 11 ( z ; τ ) = exp ( 1 4 π i τ + π i ( z + 1 2 ) ) ϑ ( z + 1 2 τ + 1 2 ; τ ) . {\displaystyle {\begin{aligned}\vartheta _{01}(z;\tau )&=\vartheta \!\left(z+{\tfrac {1}{2}};\tau \right)\\[3pt]\vartheta _{10}(z;\tau )&=\exp \left({\tfrac {1}{4}}\pi i\tau +\pi iz\right)\vartheta \left(z+{\tfrac {1}{2}}\tau ;\tau \right)\\[3pt]\vartheta _{11}(z;\tau )&=\exp \left({\tfrac {1}{4}}\pi i\tau +\pi i\left(z+{\tfrac {1}{2}}\right)\right)\vartheta \left(z+{\tfrac {1}{2}}\tau +{\tfrac {1}{2}};\tau \right).\end{aligned}}} Этим обозначениям следовали Риман и Мамфорд . Первоначальная формулировка Якоби была в терминах нома [en] q = e i π τ {\displaystyle q=e^{i{\pi }\tau }} τ {\displaystyle \tau } θ -функции записываются в виде:
θ 1 ( z ; q ) = − ϑ 11 ( z ; τ ) θ 2 ( z ; q ) = ϑ 10 ( z ; τ ) θ 3 ( z ; q ) = ϑ 00 ( z ; τ ) θ 4 ( z ; q ) = ϑ 01 ( z ; τ ) {\displaystyle {\begin{aligned}\theta _{1}(z;q)&=-\vartheta _{11}(z;\tau )\\\theta _{2}(z;q)&=\vartheta _{10}(z;\tau )\\\theta _{3}(z;q)&=\vartheta _{00}(z;\tau )\\\theta _{4}(z;q)&=\vartheta _{01}(z;\tau )\end{aligned}}} Приведённые выше определения тета-функции Якоби далеко не единственные. См. статью Тета-функции Якоби (вариации обозначений) [en]
Если мы положим z = 0 {\displaystyle z=0} τ {\displaystyle \tau } модулярных форм и для параметризации некоторых кривых.
Так называемые функции «тета-нульверт» (Theta-Nullwert ) имеют следующее представление суммы и следующее представление произведения:
ϑ 00 ( x ) = ∑ k = − ∞ ∞ x k 2 = ∏ n = 1 ∞ ( 1 − x 2 n ) ( 1 + x 2 n − 1 ) 2 {\displaystyle \vartheta _{00}(x)=\sum _{k=-\infty }^{\infty }x^{k^{2}}=\prod _{n=1}^{\infty }(1-x^{2n})(1+x^{2n-1})^{2}} ϑ 01 ( x ) = ∑ k = − ∞ ∞ ( − 1 ) k x k 2 = ∏ n = 1 ∞ ( 1 − x 2 n ) ( 1 − x 2 n − 1 ) 2 {\displaystyle \vartheta _{01}(x)=\sum _{k=-\infty }^{\infty }(-1)^{k}x^{k^{2}}=\prod _{n=1}^{\infty }(1-x^{2n})(1-x^{2n-1})^{2}} ϑ 10 ( x ) = x 1 / 4 ∑ k = − ∞ ∞ x k ( k + 1 ) = 2 x 1 / 4 ∏ n = 1 ∞ ( 1 − x 2 n ) ( 1 + x 2 n ) 2 {\displaystyle \vartheta _{10}(x)=x^{1/4}\sum _{k=-\infty }^{\infty }x^{k(k+1)}=2\,x^{1/4}\prod _{n=1}^{\infty }(1-x^{2n})(1+x^{2n})^{2}} Тета-функция удовлетворяет следующему основному соотношению с «номеном q»:
ϑ 00 [ q ( k ) ] = 2 π − 1 K ( k ) {\displaystyle \vartheta _{00}{\bigl [}q(k){\bigr ]}={\sqrt {2\pi ^{-1}K(k)}}} ϑ 01 [ q ( k ) ] = 1 − k 2 4 2 π − 1 K ( k ) {\displaystyle \vartheta _{01}{\bigl [}q(k){\bigr ]}={\sqrt[{4}]{1-k^{2}}}{\sqrt {2\pi ^{-1}K(k)}}} ϑ 10 [ q ( k ) ] = | k | 2 π − 1 K ( k ) {\displaystyle \vartheta _{10}{\bigl [}q(k){\bigr ]}={\sqrt {|k|}}{\sqrt {2\pi ^{-1}K(k)}}} q ( k ) = exp [ − π K ( 1 − k 2 ) / K ( k ) ] {\displaystyle q(k)=\exp {\bigl [}-\pi \,K({\sqrt {1-k^{2}}})/K(k){\bigr ]}} Следующие две формулы определяют полный эллиптический интеграл первого типа и согласуются друг с другом:
K ( ε ) = ∫ 0 1 1 ( 1 − x 2 ) ( 1 − ε 2 x 2 ) d x {\displaystyle K(\varepsilon )=\int _{0}^{1}{\frac {1}{\sqrt {(1-x^{2})(1-\varepsilon ^{2}x^{2})}}}\,\mathrm {d} x} K ( ε ) = ∫ 0 π / 2 1 1 − ε 2 sin ( φ ) 2 d φ {\displaystyle K(\varepsilon )=\int _{0}^{\pi /2}{\frac {1}{\sqrt {1-\varepsilon ^{2}\sin(\varphi )^{2}}}}\,\mathrm {d} \varphi } В частности Тождества Якоби
ϑ 00 ( 0 ; τ ) 4 = ϑ 01 ( 0 ; τ ) 4 + ϑ 10 ( 0 ; τ ) 4 {\displaystyle \vartheta _{00}(0;\tau )^{4}=\vartheta _{01}(0;\tau )^{4}+\vartheta _{10}(0;\tau )^{4}} ϑ 00 ( q ) 4 = ϑ 01 ( q ) 4 + ϑ 10 ( q ) 4 {\displaystyle \vartheta _{00}(q)^{4}=\vartheta _{01}(q)^{4}+\vartheta _{10}(q)^{4}} Эта формула представляет собой кривой Ферма четвертой степени.
Тождества Якоби также возникает как комбинация трех квадратичных соотношений:
2 ϑ 00 ( q 2 ) 2 = ϑ 00 ( q ) 2 + ϑ 01 ( q ) 2 {\displaystyle 2\,\vartheta _{00}(q^{2})^{2}=\vartheta _{00}(q)^{2}+\vartheta _{01}(q)^{2}} 2 ϑ 10 ( q 2 ) 2 = ϑ 00 ( q ) 2 − ϑ 01 ( q ) 2 {\displaystyle 2\,\vartheta _{10}(q^{2})^{2}=\vartheta _{00}(q)^{2}-\vartheta _{01}(q)^{2}} ϑ 10 ( q ) 2 = 2 ϑ 10 ( q 2 ) ϑ 00 ( q 2 ) {\displaystyle \vartheta _{10}(q)^{2}=2\,\vartheta _{10}(q^{2})\,\vartheta _{00}(q^{2})} Объединение этих трех формул дает следующую формулу:
ϑ 10 ( q ) 4 = ϑ 00 ( q ) 4 − ϑ 01 ( q ) 4 {\displaystyle \vartheta _{10}(q)^{4}=\vartheta _{00}(q)^{4}-\vartheta _{01}(q)^{4}} Тождества Якоби описывают, как тета-функции преобразуются модулярной группой , которая порождается отображениями τ ↦ τ + 1 {\displaystyle \tau \mapsto \tau +1} τ ↦ − 1 τ {\displaystyle \tau \mapsto -{\tfrac {1}{\tau }}} τ {\displaystyle \tau } 1 2 {\displaystyle {\tfrac {1}{2}}} z ( n ≡ n 2 {\displaystyle n\equiv n^{2}} mod 2). Во втором случае положим
α = ( − i τ ) 1 2 exp ( π τ i z 2 ) . {\displaystyle \alpha =(-i\tau )^{\frac {1}{2}}\exp \left({\frac {\pi }{\tau }}iz^{2}\right).} Тогда
ϑ 00 ( z τ ; − 1 τ ) = α ϑ 00 ( z ; τ ) ϑ 01 ( z τ ; − 1 τ ) = α ϑ 10 ( z ; τ ) ϑ 10 ( z τ ; − 1 τ ) = α ϑ 01 ( z ; τ ) ϑ 11 ( z τ ; − 1 τ ) = − i α ϑ 11 ( z ; τ ) . {\displaystyle {\begin{aligned}\vartheta _{00}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=\alpha \,\vartheta _{00}(z;\tau )\quad &\vartheta _{01}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=\alpha \,\vartheta _{10}(z;\tau )\\[3pt]\vartheta _{10}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=\alpha \,\vartheta _{01}(z;\tau )\quad &\vartheta _{11}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=-i\alpha \,\vartheta _{11}(z;\tau ).\end{aligned}}} Вместо выражения тета-функций в терминах z и τ {\displaystyle \tau } w и нома [en] q , где w = e π i z {\displaystyle w=e^{\pi {i}z}} q = e π i τ {\displaystyle q=e^{\pi {i}\tau }}
ϑ 00 ( w , q ) = ∑ n = − ∞ ∞ ( w 2 ) n q n 2 ϑ 01 ( w , q ) = ∑ n = − ∞ ∞ ( − 1 ) n ( w 2 ) n q n 2 ϑ 10 ( w , q ) = ∑ n = − ∞ ∞ ( w 2 ) n + 1 2 q ( n + 1 2 ) 2 ϑ 11 ( w , q ) = i ∑ n = − ∞ ∞ ( − 1 ) n ( w 2 ) n + 1 2 q ( n + 1 2 ) 2 . {\displaystyle {\begin{aligned}\vartheta _{00}(w,q)&=\sum _{n=-\infty }^{\infty }(w^{2})^{n}q^{n^{2}}\quad &\vartheta _{01}(w,q)&=\sum _{n=-\infty }^{\infty }(-1)^{n}(w^{2})^{n}q^{n^{2}}\\[3pt]\vartheta _{10}(w,q)&=\sum _{n=-\infty }^{\infty }(w^{2})^{n+{\frac {1}{2}}}q^{\left(n+{\frac {1}{2}}\right)^{2}}\quad &\vartheta _{11}(w,q)&=i\sum _{n=-\infty }^{\infty }(-1)^{n}(w^{2})^{n+{\frac {1}{2}}}q^{\left(n+{\frac {1}{2}}\right)^{2}}.\end{aligned}}} Мы видим, что тета-функции можно определить в терминах w и q без прямой ссылки на экспоненциальную функцию. Формулы могут быть использованы, поэтому, для определения тета-функций над другими полями , где экспоненциальная функция может быть не везде определена, такими как поле p -адических чисел
Тройное произведение Якоби (специальный случай тождеств Макдональда [en] w и q с | q | < 1 {\displaystyle |q|<1} w ≠ 0 {\displaystyle w\neq 0}
∏ m = 1 ∞ ( 1 − q 2 m ) ( 1 + w 2 q 2 m − 1 ) ( 1 + w − 2 q 2 m − 1 ) = ∑ n = − ∞ ∞ w 2 n q n 2 . {\displaystyle \prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+w^{2}q^{2m-1}\right)\left(1+w^{-2}q^{2m-1}\right)=\sum _{n=-\infty }^{\infty }w^{2n}q^{n^{2}}.} Это можно доказать элементарными средствами, как, например, в книге Харди и Райта An Introduction to the Theory of Numbers [en]
Если мы выразим тета-функцию в терминах томов q = e π i τ {\displaystyle q=e^{\pi {i}\tau }} w = e π i z {\displaystyle w=e^{\pi {i}z}}
ϑ ( z ; τ ) = ∑ n = − ∞ ∞ exp ( π i τ n 2 ) exp ( 2 π i z n ) = ∑ n = − ∞ ∞ w 2 n q n 2 . {\displaystyle \vartheta (z;\tau )=\sum _{n=-\infty }^{\infty }\exp(\pi i\tau n^{2})\exp(2\pi izn)=\sum _{n=-\infty }^{\infty }w^{2n}q^{n^{2}}.} Мы поэтому получаем формулу произведения для тета-функции вида
ϑ ( z ; τ ) = ∏ m = 1 ∞ ( 1 − exp ( 2 m π i τ ) ) ( 1 + exp ( ( 2 m − 1 ) π i τ + 2 π i z ) ) ( 1 + exp ( ( 2 m − 1 ) π i τ − 2 π i z ) ) . {\displaystyle \vartheta (z;\tau )=\prod _{m=1}^{\infty }{\big (}1-\exp(2m\pi i\tau ){\big )}{\Big (}1+\exp {\big (}(2m-1)\pi i\tau +2\pi iz{\big )}{\Big )}{\Big (}1+\exp {\big (}(2m-1)\pi i\tau -2\pi iz{\big )}{\Big )}.} В терминах w и q :
ϑ ( z ; τ ) = ∏ m = 1 ∞ ( 1 − q 2 m ) ( 1 + q 2 m − 1 w 2 ) ( 1 + q 2 m − 1 w 2 ) = ( q 2 ; q 2 ) ∞ ( − w 2 q ; q 2 ) ∞ ( − q w 2 ; q 2 ) ∞ = ( q 2 ; q 2 ) ∞ θ ( − w 2 q ; q 2 ) {\displaystyle {\begin{aligned}\vartheta (z;\tau )&=\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+q^{2m-1}w^{2}\right)\left(1+{\frac {q^{2m-1}}{w^{2}}}\right)\\&=\left(q^{2};q^{2}\right)_{\infty }\,\left(-w^{2}q;q^{2}\right)_{\infty }\,\left(-{\frac {q}{w^{2}}};q^{2}\right)_{\infty }\\&=\left(q^{2};q^{2}\right)_{\infty }\,\theta \left(-w^{2}q;q^{2}\right)\end{aligned}}} где ( ; ) ∞ {\displaystyle (~~;~~)_{\infty }} q -символом Похгаммера θ ( ; ) {\displaystyle \theta (~~;~~)} q -тета-функцией[en]
∏ m = 1 ∞ ( 1 − q 2 m ) ( 1 + ( w 2 + w − 2 ) q 2 m − 1 + q 4 m − 2 ) , {\displaystyle \prod _{m=1}^{\infty }\left(1-q^{2m}\right){\Big (}1+\left(w^{2}+w^{-2}\right)q^{2m-1}+q^{4m-2}{\Big )},} что можно также переписать в виде
ϑ ( z ∣ q ) = ∏ m = 1 ∞ ( 1 − q 2 m ) ( 1 + 2 cos ( 2 π z ) q 2 m − 1 + q 4 m − 2 ) . {\displaystyle \vartheta (z\mid q)=\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+2\cos(2\pi z)q^{2m-1}+q^{4m-2}\right).} Эта формула верна для общего случая, но представляет особый интерес при вещественных z . Аналогичные формулы произведений для дополнительных тета-функций
ϑ 01 ( z ∣ q ) = ∏ m = 1 ∞ ( 1 − q 2 m ) ( 1 − 2 cos ( 2 π z ) q 2 m − 1 + q 4 m − 2 ) , ϑ 10 ( z ∣ q ) = 2 q 1 4 cos ( π z ) ∏ m = 1 ∞ ( 1 − q 2 m ) ( 1 + 2 cos ( 2 π z ) q 2 m + q 4 m ) , ϑ 11 ( z ∣ q ) = − 2 q 1 4 sin ( π z ) ∏ m = 1 ∞ ( 1 − q 2 m ) ( 1 − 2 cos ( 2 π z ) q 2 m + q 4 m ) . {\displaystyle {\begin{aligned}\vartheta _{01}(z\mid q)&=\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1-2\cos(2\pi z)q^{2m-1}+q^{4m-2}\right),\\[3pt]\vartheta _{10}(z\mid q)&=2q^{\frac {1}{4}}\cos(\pi z)\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+2\cos(2\pi z)q^{2m}+q^{4m}\right),\\[3pt]\vartheta _{11}(z\mid q)&=-2q^{\frac {1}{4}}\sin(\pi z)\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1-2\cos(2\pi z)q^{2m}+q^{4m}\right).\end{aligned}}} Тета-функции Якоби имеют следующие интегральные представления:
ϑ 00 ( z ; τ ) = − i ∫ i − ∞ i + ∞ e i π τ u 2 cos ( 2 u z + π u ) sin ( π u ) d u ; ϑ 01 ( z ; τ ) = − i ∫ i − ∞ i + ∞ e i π τ u 2 cos ( 2 u z ) sin ( π u ) d u ; ϑ 10 ( z ; τ ) = − i e i z + 1 4 i π τ ∫ i − ∞ i + ∞ e i π τ u 2 cos ( 2 u z + π u + π τ u ) sin ( π u ) d u ; ϑ 11 ( z ; τ ) = e i z + 1 4 i π τ ∫ i − ∞ i + ∞ e i π τ u 2 cos ( 2 u z + π τ u ) sin ( π u ) d u . {\displaystyle {\begin{aligned}\vartheta _{00}(z;\tau )&=-i\int _{i-\infty }^{i+\infty }{e^{i\pi \tau u^{2}}{\frac {\cos(2uz+\pi u)}{\sin(\pi u)}}}\mathrm {d} u;\\[6pt]\vartheta _{01}(z;\tau )&=-i\int _{i-\infty }^{i+\infty }{e^{i\pi \tau u^{2}}{\frac {\cos(2uz)}{\sin(\pi u)}}}\mathrm {d} u;\\[6pt]\vartheta _{10}(z;\tau )&=-ie^{iz+{\frac {1}{4}}i\pi \tau }\int _{i-\infty }^{i+\infty }{e^{i\pi \tau u^{2}}{\frac {\cos(2uz+\pi u+\pi \tau u)}{\sin(\pi u)}}}\mathrm {d} u;\\[6pt]\vartheta _{11}(z;\tau )&=e^{iz+{\frac {1}{4}}i\pi \tau }\int _{i-\infty }^{i+\infty }{e^{i\pi \tau u^{2}}{\frac {\cos(2uz+\pi \tau u)}{\sin(\pi u)}}}\mathrm {d} u.\end{aligned}}} См. статью Джинхи Йи (2004)[2]
ϑ 00 ( e − π x ) = ϑ ( 0 ; i x ) = θ 3 ( 0 ; e − π x ) = ∑ n = − ∞ ∞ exp ( − π x n 2 ) {\displaystyle \vartheta _{00}(e^{-\pi x})=\vartheta (0;ix)=\theta _{3}(0;e^{-\pi x})=\sum _{n=-\infty }^{\infty }\exp(-\pi xn^{2})} ϑ 01 ( e − π x ) = θ 4 ( 0 ; e − π x ) = ∑ n = − ∞ ∞ ( − 1 ) n exp ( − π x n 2 ) {\displaystyle \vartheta _{01}(e^{-\pi x})=\theta _{4}(0;e^{-\pi x})=\sum _{n=-\infty }^{\infty }(-1)^{n}\exp(-\pi xn^{2})} ϑ 10 ( e − π x ) = θ 2 ( 0 ; e − π x ) = ∑ n = − ∞ ∞ exp [ − π x ( n + 1 2 ) 2 ] {\displaystyle \vartheta _{10}(e^{-\pi x})=\theta _{2}(0;e^{-\pi x})=\sum _{n=-\infty }^{\infty }\exp {\bigl [}-\pi x(n+{\tfrac {1}{2}})^{2}{\bigr ]}} В следующей таблице приведены лемнискатические значения функций ϑ₁₀(x ) и ϑ₀₀(x ) :
x ϑ₁₀(x ) ϑ₀₀(x ) e − π {\displaystyle {\text{e}}^{-\pi }} π 4 Γ ( 3 4 ) − 1 2 − 1 / 4 = G {\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-1/4}={\sqrt {G}}} π 4 Γ ( 3 4 ) − 1 = 2 1 / 4 G {\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}=2^{1/4}{\sqrt {G}}} e − 2 π {\displaystyle {\text{e}}^{-2\pi }} π 4 Γ ( 3 4 ) − 1 2 − 3 / 4 2 − 1 {\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-3/4}{\sqrt {{\sqrt {2}}-1}}} π 4 Γ ( 3 4 ) − 1 2 − 3 / 4 2 + 1 {\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-3/4}{\sqrt {{\sqrt {2}}+1}}} e − 3 π {\displaystyle {\text{e}}^{-3\pi }} π 4 Γ ( 3 4 ) − 1 2 − 3 / 2 3 − 3 / 8 3 − 1 ( 3 + 1 − 12 4 ) {\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-3/2}3^{-3/8}{\sqrt {{\sqrt {3}}-1}}({\sqrt {3}}+1-{\sqrt[{4}]{12}})} π 4 Γ ( 3 4 ) − 1 2 − 1 / 4 3 − 3 / 8 3 + 1 {\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-1/4}3^{-3/8}{\sqrt {{\sqrt {3}}+1}}} e − 4 π {\displaystyle {\text{e}}^{-4\pi }} π 4 Γ ( 3 4 ) − 1 2 − 5 / 4 ( 2 4 − 1 ) {\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/4}({\sqrt[{4}]{2}}-1)} π 4 Γ ( 3 4 ) − 1 2 − 5 / 4 ( 2 4 + 1 ) {\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/4}({\sqrt[{4}]{2}}+1)} e − 5 π {\displaystyle {\text{e}}^{-5\pi }} π 4 Γ ( 3 4 ) − 1 2 − 5 / 4 5 − 1 / 2 ( 5 4 − 1 ) 2 Φ − 1 / 2 {\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/4}5^{-1/2}({\sqrt[{4}]{5}}-1)^{2}\Phi ^{-1/2}} π 4 Γ ( 3 4 ) − 1 5 − 1 / 2 Φ 3 / 2 {\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}5^{-1/2}\Phi ^{3/2}}
Дополнительные значения для ϑ₀₀(x ) :
ϑ 00 ( e − 6 π ) = π 4 Γ ( 3 4 ) − 1 2 − 2 3 − 3 / 8 cot ( 1 24 π ) ( 3 4 + 1 ) ( 3 + 1 − 12 4 ) {\displaystyle \vartheta _{00}({\text{e}}^{-6\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-2}3^{-3/8}{\sqrt {\cot({\tfrac {1}{24}}\pi )}}({\sqrt[{4}]{3}}+1)({\sqrt {3}}+1-{\sqrt[{4}]{12}})} ϑ 00 ( e − 7 π ) = π 4 Γ ( 3 4 ) − 1 2 − 5 / 8 7 − 7 / 16 3 + 7 4 5 − 7 + 28 4 {\displaystyle \vartheta _{00}({\text{e}}^{-7\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/8}7^{-7/16}{\sqrt[{4}]{3+{\sqrt {7}}}}{\sqrt {5-{\sqrt {7}}+{\sqrt[{4}]{28}}}}} ϑ 00 ( e − 8 π ) = π 4 Γ ( 3 4 ) − 1 2 − 2 ( 2 + 2 + 2 7 / 8 ) {\displaystyle \vartheta _{00}({\text{e}}^{-8\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-2}({\sqrt {2+{\sqrt {2}}}}+2^{7/8})} ϑ 00 ( e − 9 π ) = π 4 Γ ( 3 4 ) − 1 3 − 1 ( 2 3 + 2 3 + 1 ) {\displaystyle \vartheta _{00}({\text{e}}^{-9\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}3^{-1}({\sqrt[{3}]{2{\sqrt {3}}+2}}+1)} ϑ 00 ( e − 10 π ) = π 4 Γ ( 3 4 ) − 1 5 − 1 / 2 Φ 3 / 2 cos [ 1 4 arcsin ( Φ − 12 ) ] {\displaystyle \vartheta _{00}({\text{e}}^{-10\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}5^{-1/2}\Phi ^{3/2}\cos {\bigl [}{\tfrac {1}{4}}\arcsin {\bigl (}\Phi ^{-12}{\bigr )}{\bigr ]}} ϑ 00 ( e − 11 π ) = π 4 Γ ( 3 4 ) − 1 2 − 5 / 4 11 − 5 / 8 11 + 3 { 4 + 11 − 3 3 tanh [ 1 4 arcosh ( 7 4 ) + 1 2 artanh ( 4 9 3 ) − 1 6 artanh ( 1 27 3 ) ] } {\displaystyle \vartheta _{00}({\text{e}}^{-11\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/4}11^{-5/8}{\sqrt {{\sqrt {11}}+3}}\,{\bigl \{}4+{\sqrt {11}}-3{\sqrt {3}}\tanh {\bigl [}{\tfrac {1}{4}}\operatorname {arcosh} ({\tfrac {7}{4}})+{\tfrac {1}{2}}\operatorname {artanh} ({\tfrac {4}{9}}{\sqrt {3}})-{\tfrac {1}{6}}\operatorname {artanh} ({\tfrac {1}{27}}{\sqrt {3}}){\bigr ]}{\bigr \}}} ϑ 00 ( e − 12 π ) = π 4 Γ ( 3 4 ) − 1 2 − 2 3 − 3 / 8 cot ( 1 24 π ) ( 3 4 + 1 ) ( 3 + 1 − 12 4 ) cos { 1 2 arcsin [ 1 2 ( 2 + 3 ) ( 3 − 2 ) 2 ( 2 − 1 ) 2 ( 3 4 − 1 ) 4 ] } {\displaystyle \vartheta _{00}({\text{e}}^{-12\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-2}3^{-3/8}{\sqrt {\cot({\tfrac {1}{24}}\pi )}}({\sqrt[{4}]{3}}+1)({\sqrt {3}}+1-{\sqrt[{4}]{12}})\cos {\bigl \{}{\tfrac {1}{2}}\arcsin {\bigl [}{\tfrac {1}{2}}(2+{\sqrt {3}})({\sqrt {3}}-{\sqrt {2}})^{2}({\sqrt {2}}-1)^{2}({\sqrt[{4}]{3}}-1)^{4}{\bigr ]}{\bigr \}}} ϑ 00 ( e − 13 π ) = π 4 Γ ( 3 4 ) − 1 13 − 1 / 2 5 13 + 18 { 1 6 ( 5 39 − 17 3 ) coth [ 1 3 artanh ( 6 11 3 ) − 1 2 arcosh ( 4 13 13 ) ] − 1 2 ( 13 − 3 ) } {\displaystyle \vartheta _{00}({\text{e}}^{-13\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}13^{-1/2}{\sqrt {5{\sqrt {13}}+18}}\,{\bigl \{}{\tfrac {1}{6}}(5{\sqrt {39}}-17{\sqrt {3}})\coth {\bigl [}{\tfrac {1}{3}}\operatorname {artanh} ({\tfrac {6}{11}}{\sqrt {3}})-{\tfrac {1}{2}}\operatorname {arcosh} {\bigl (}{\tfrac {4}{13}}{\sqrt {13}}{\bigr )}{\bigr ]}-{\tfrac {1}{2}}({\sqrt {13}}-3){\bigr \}}} ϑ 00 ( e − 14 π ) = π 4 Γ ( 3 4 ) − 1 2 − 5 / 8 7 − 7 / 16 3 + 7 4 5 − 7 + 28 4 cos { 1 4 arcsin [ ( 1 4 14 + 1 4 2 − 1 2 7 4 ) 12 ] } {\displaystyle \vartheta _{00}({\text{e}}^{-14\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/8}7^{-7/16}{\sqrt[{4}]{3+{\sqrt {7}}}}{\sqrt {5-{\sqrt {7}}+{\sqrt[{4}]{28}}}}\,\cos {\bigl \{}{\tfrac {1}{4}}\arcsin {\bigl [}({\tfrac {1}{4}}{\sqrt {14}}+{\tfrac {1}{4}}{\sqrt {2}}-{\tfrac {1}{2}}{\sqrt[{4}]{7}})^{12}{\bigr ]}{\bigr \}}} ϑ 00 ( e − 15 π ) = π 4 Γ ( 3 4 ) − 1 3 − 1 / 2 5 − 1 / 2 Φ 3 / 2 ( 2 1 + Φ − 8 + Φ − 16 + 2 + Φ − 8 + 1 − Φ − 8 ) 1 / 2 {\displaystyle \vartheta _{00}({\text{e}}^{-15\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}3^{-1/2}5^{-1/2}\Phi ^{3/2}{\bigl (}{\sqrt {2{\sqrt {1+\Phi ^{-8}+\Phi ^{-16}}}+2+\Phi ^{-8}}}+{\sqrt {1-\Phi ^{-8}}}{\bigr )}^{1/2}} ϑ 00 ( e − 16 π ) = π 4 Γ ( 3 4 ) − 1 [ 2 − 9 / 4 ( 2 4 + 1 ) + 2 − 23 / 16 2 + 1 4 ] {\displaystyle \vartheta _{00}({\text{e}}^{-16\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}{\bigl [}2^{-9/4}({\sqrt[{4}]{2}}+1)+2^{-23/16}{\sqrt[{4}]{{\sqrt {2}}+1}}{\bigr ]}} ϑ 00 ( e − 17 π ) = π 4 Γ ( 3 4 ) − 1 2 − 3 / 2 17 − 1 / 2 [ ( 17 4 + 1 ) 17 − 1 + 272 8 17 + 3 ] {\displaystyle \vartheta _{00}({\text{e}}^{-17\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-3/2}17^{-1/2}{\bigl [}({\sqrt[{4}]{17}}+1){\sqrt {{\sqrt {17}}-1}}+{\sqrt[{8}]{272}}{\sqrt {{\sqrt {17}}+3}}{\bigr ]}} ϑ 00 ( e − 18 π ) = π 4 Γ ( 3 4 ) − 1 3 − 1 ( 2 3 + 2 3 + 1 ) cos ⟨ 1 4 arcsin { [ 2 3 − 3 − 6 ( 2 − 3 ) 5 / 6 + 2 ( 2 − 3 ) 7 / 6 ] 4 } ⟩ {\displaystyle \vartheta _{00}({\text{e}}^{-18\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}3^{-1}({\sqrt[{3}]{2{\sqrt {3}}+2}}+1)\cos {\bigl \langle }{\tfrac {1}{4}}\arcsin {\bigl \{}{\bigl [}2{\sqrt {3}}-3-{\sqrt {6}}(2-{\sqrt {3}})^{5/6}+{\sqrt {2}}(2-{\sqrt {3}})^{7/6}{\bigr ]}^{4}{\bigr \}}{\bigr \rangle }} И с греческой буквой Φ = ( 5 + 1 ) / 2 {\displaystyle \Phi =({\sqrt {5}}+1)/2} Золотое сечение . Символом G {\displaystyle G} постоянная Гаусса , которая представляет собой отношение лемнискатической константы к числу π . Только что показанные значения были исследованы южнокорейским математиком Джинхи Йи из Пусанского национального университета (부산 대학교). Их результаты впоследствии были опубликованы в Журнале математического анализа и приложений. Кроме того, применяются следующие значения:
ϑ 00 [ exp ( − 1 2 π ) ] = π 4 Γ ( 3 4 ) − 1 2 − 1 / 4 2 + 1 {\displaystyle \vartheta _{00}[\exp(-{\tfrac {1}{2}}\pi )]={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-1/4}{\sqrt {{\sqrt {2}}+1}}} ϑ 00 [ exp ( − 1 3 π ) ] = π 4 Γ ( 3 4 ) − 1 2 − 1 / 4 3 1 / 8 3 + 1 {\displaystyle \vartheta _{00}[\exp(-{\tfrac {1}{3}}\pi )]={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-1/4}3^{1/8}{\sqrt {{\sqrt {3}}+1}}} Эти два значения можно определить непосредственно с помощью формулы суммы Пуассона:
ϑ 00 [ exp ( − π / y ) ] = y ϑ 00 [ exp ( − π y ) ] {\displaystyle \vartheta _{00}[\exp(-\pi /y)]={\sqrt {y}}\,\vartheta _{00}[\exp(-\pi y)]} Функция ϑ₀₀ имеет следующие эквиангармонические значения функции:
ϑ 00 [ exp ( − 3 π ) ] = π − 1 / 2 2 − 1 / 6 3 − 1 / 8 β ( 1 3 ) 1 / 2 {\displaystyle \vartheta _{00}[\exp(-{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-1/6}3^{-1/8}\beta ({\tfrac {1}{3}})^{1/2}} ϑ 00 [ exp ( − 2 3 π ) ] = π − 1 / 2 2 − 1 / 6 3 − 1 / 8 β ( 1 3 ) 1 / 2 cos ( 1 24 π ) {\displaystyle \vartheta _{00}[\exp(-2{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-1/6}3^{-1/8}\beta ({\tfrac {1}{3}})^{1/2}\cos({\tfrac {1}{24}}\pi )} ϑ 00 [ exp ( − 3 3 π ) ] = π − 1 / 2 2 − 1 / 6 3 − 7 / 8 β ( 1 3 ) 1 / 2 ( 2 3 + 1 ) {\displaystyle \vartheta _{00}[\exp(-3{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-1/6}3^{-7/8}\beta ({\tfrac {1}{3}})^{1/2}({\sqrt[{3}]{2}}+1)} ϑ 00 [ exp ( − 4 3 π ) ] = π − 1 / 2 2 − 7 / 6 3 − 1 / 8 β ( 1 3 ) 1 / 2 [ 1 + cos ( 1 12 π ) ] {\displaystyle \vartheta _{00}[\exp(-4{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-7/6}3^{-1/8}\beta ({\tfrac {1}{3}})^{1/2}[1+{\sqrt {\cos({\tfrac {1}{12}}\pi )}}]} ϑ 00 [ exp ( − 5 3 π ) ] = π − 1 / 2 2 − 1 / 6 3 − 9 / 8 β ( 1 3 ) 1 / 2 sin ( 1 5 π ) ( 2 5 100 3 + 2 5 10 3 + 3 5 5 + 1 ) {\displaystyle \vartheta _{00}[\exp(-5{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-1/6}3^{-9/8}\beta ({\tfrac {1}{3}})^{1/2}\sin({\tfrac {1}{5}}\pi )({\tfrac {2}{5}}{\sqrt[{3}]{100}}+{\tfrac {2}{5}}{\sqrt[{3}]{10}}+{\tfrac {3}{5}}{\sqrt {5}}+1)} Некоторые эквиангармонические значения тета-функции были исследованы, в частности, математиками Брюсом Карлом Берндтом и Орсом Ребаком.
Значения тета над факториалами восьмых [ править | править код ] Значения функции вида ϑ₀₁ :
ϑ 01 [ exp ( − 2 π ) ] = 2 − 1 / 4 π − 1 / 2 cos ( 1 8 π ) β ( 3 8 ) {\displaystyle \vartheta _{01}[\exp(-{\sqrt {2}}\,\pi )]=2^{-1/4}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}} ϑ 01 [ exp ( − 3 2 π ) ] = 2 − 1 / 4 3 − 1 / 2 π − 1 / 2 cos ( 1 8 π ) β ( 3 8 ) 3 + 2 {\displaystyle \vartheta _{01}[\exp(-3{\sqrt {2}}\,\pi )]=2^{-1/4}3^{-1/2}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}\,{\sqrt {{\sqrt {3}}+{\sqrt {2}}}}} ϑ 01 [ exp ( − 1 3 2 π ) ] = 2 − 1 / 4 π − 1 / 2 cos ( 1 8 π ) β ( 3 8 ) 3 − 2 {\displaystyle \vartheta _{01}[\exp(-{\tfrac {1}{3}}{\sqrt {2}}\,\pi )]=2^{-1/4}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}\,{\sqrt {{\sqrt {3}}-{\sqrt {2}}}}} ϑ 01 [ exp ( − 5 2 π ) ] = 2 − 1 / 4 5 − 1 / 2 π − 1 / 2 cos ( 1 8 π ) β ( 3 8 ) { 4 3 2 cos ( 1 10 π ) cosh [ 1 3 artanh ( 3 8 6 ) ] + 1 3 tan ( 1 5 π ) } {\displaystyle \vartheta _{01}[\exp(-5{\sqrt {2}}\,\pi )]=2^{-1/4}5^{-1/2}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}\,{\bigl \{}{\tfrac {4}{3}}{\sqrt {2}}\cos({\tfrac {1}{10}}\pi )\cosh[{\tfrac {1}{3}}\operatorname {artanh} ({\tfrac {3}{8}}{\sqrt {6}})]+{\tfrac {1}{3}}\tan({\tfrac {1}{5}}\pi ){\bigr \}}} ϑ 01 [ exp ( − 1 5 2 π ) ] = 2 − 1 / 4 π − 1 / 2 cos ( 1 8 π ) β ( 3 8 ) { 4 3 2 sin ( 1 5 π ) cosh [ 1 3 artanh ( 3 8 6 ) ] − 1 3 cot ( 1 10 π ) } {\displaystyle \vartheta _{01}[\exp(-{\tfrac {1}{5}}{\sqrt {2}}\,\pi )]=2^{-1/4}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}\,{\bigl \{}{\tfrac {4}{3}}{\sqrt {2}}\sin({\tfrac {1}{5}}\pi )\cosh[{\tfrac {1}{3}}\operatorname {artanh} ({\tfrac {3}{8}}{\sqrt {6}})]-{\tfrac {1}{3}}\cot({\tfrac {1}{10}}\pi ){\bigr \}}} Следующие два тождества для рядов доказал Иштван Мезо[3]
ϑ 4 2 ( q ) = i q 1 4 ∑ k = − ∞ ∞ q 2 k 2 − k ϑ 1 ( 2 k − 1 2 i ln q , q ) , ϑ 4 2 ( q ) = ∑ k = − ∞ ∞ q 2 k 2 ϑ 4 ( k ln q i , q ) . {\displaystyle {\begin{aligned}\vartheta _{4}^{2}(q)&=iq^{\frac {1}{4}}\sum _{k=-\infty }^{\infty }q^{2k^{2}-k}\vartheta _{1}\left({\frac {2k-1}{2i}}\ln q,q\right),\\[6pt]\vartheta _{4}^{2}(q)&=\sum _{k=-\infty }^{\infty }q^{2k^{2}}\vartheta _{4}\left({\frac {k\ln q}{i}},q\right).\end{aligned}}} Эти отношения выполняются для всех 0 < q < 1 . Фиксируя значения q , мы получим следующие свободные от параметров суммы
π e π 2 ⋅ 1 Γ 2 ( 3 4 ) = i ∑ k = − ∞ ∞ e π ( k − 2 k 2 ) ϑ 1 ( i π 2 ( 2 k − 1 ) , e − π ) , π 2 ⋅ 1 Γ 2 ( 3 4 ) = ∑ k = − ∞ ∞ ϑ 4 ( i k π , e − π ) e 2 π k 2 {\displaystyle {\begin{aligned}{\sqrt {\frac {\pi {\sqrt {e^{\pi }}}}{2}}}\cdot {\frac {1}{\Gamma ^{2}\left({\frac {3}{4}}\right)}}&=i\sum _{k=-\infty }^{\infty }e^{\pi \left(k-2k^{2}\right)}\vartheta _{1}\left({\frac {i\pi }{2}}(2k-1),e^{-\pi }\right),\\[6pt]{\sqrt {\frac {\pi }{2}}}\cdot {\frac {1}{\Gamma ^{2}\left({\frac {3}{4}}\right)}}&=\sum _{k=-\infty }^{\infty }{\frac {\vartheta _{4}\left(ik\pi ,e^{-\pi }\right)}{e^{2\pi k^{2}}}}\end{aligned}}} Все нули тета-функций Якоби являются простыми нулями и задаются следующим образом:
ϑ ( z , τ ) = ϑ 3 ( z , τ ) = 0 ⟺ z = m + n τ + 1 2 + τ 2 ϑ 1 ( z , τ ) = 0 ⟺ z = m + n τ ϑ 2 ( z , τ ) = 0 ⟺ z = m + n τ + 1 2 ϑ 4 ( z , τ ) = 0 ⟺ z = m + n τ + τ 2 {\displaystyle {\begin{aligned}\vartheta (z,\tau )=\vartheta _{3}(z,\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau +{\frac {1}{2}}+{\frac {\tau }{2}}\\[3pt]\vartheta _{1}(z,\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau \\[3pt]\vartheta _{2}(z,\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau +{\frac {1}{2}}\\[3pt]\vartheta _{4}(z,\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau +{\frac {\tau }{2}}\end{aligned}}} где m , n являются произвольными целыми.
Соотношение
ϑ ( 0 ; − 1 τ ) = ( − i τ ) 1 2 ϑ ( 0 ; τ ) {\displaystyle \vartheta \left(0;-{\frac {1}{\tau }}\right)=(-i\tau )^{\frac {1}{2}}\vartheta (0;\tau )} использовал Риман для доказательства функционального уравнения для дзета-функции Римана посредством преобразования Меллина
Γ ( s 2 ) π − s 2 ζ ( s ) = 1 2 ∫ 0 ∞ ( ϑ ( 0 ; i t ) − 1 ) t s 2 d t t {\displaystyle \Gamma \left({\frac {s}{2}}\right)\pi ^{-{\frac {s}{2}}}\zeta (s)={\frac {1}{2}}\int _{0}^{\infty }{\big (}\vartheta (0;it)-1{\big )}t^{\frac {s}{2}}{\frac {\mathrm {d} t}{t}}} и можно показать, что преобразование инвариантно относительно замены s на 1 − s . Cоответствующий интеграл для z ≠ 0дзета-функции Гурвица .
Связь с эллиптической функцией Вейерштрасса [ править | править код ] Тета-функции использовал Якоби для построения (в виде, приспособленном для упрощения вычислений) его эллиптических функций как частные вышеприведённых четырёх тета-функций, и он мог их использовать также для построения эллиптических функций Вейерштрасса , поскольку
℘ ( z ; τ ) = − ( log ϑ 11 ( z ; τ ) ) ″ + c {\displaystyle \wp (z;\tau )=-{\big (}\log \vartheta _{11}(z;\tau ){\big )}''+c} где вторая производная берётся по z , а константа c определена так, что ряд Лорана функции ℘(z ) в точке z = 0
Четвёртая тета-функция – а тогда и остальные – неразрывно связана с q -гамма-функцией Джексона[en] [4]
( Γ q 2 ( x ) Γ q 2 ( 1 − x ) ) − 1 = q 2 x ( 1 − x ) ( q − 2 ; q − 2 ) ∞ 3 ( q 2 − 1 ) ϑ 4 ( 1 2 i ( 1 − 2 x ) log q , 1 q ) . {\displaystyle \left(\Gamma _{q^{2}}(x)\Gamma _{q^{2}}(1-x)\right)^{-1}={\frac {q^{2x(1-x)}}{\left(q^{-2};q^{-2}\right)_{\infty }^{3}\left(q^{2}-1\right)}}\vartheta _{4}\left({\frac {1}{2i}}(1-2x)\log q,{\frac {1}{q}}\right).} Пусть η ( τ ) {\displaystyle \eta (\tau )} эта-функция Дедекинда [en] ном [en] q = e π i τ {\displaystyle q=e^{\pi {i}\tau }}
θ 2 ( 0 , q ) = ϑ 10 ( 0 ; τ ) = 2 η 2 ( 2 τ ) η ( τ ) , θ 3 ( 0 , q ) = ϑ 00 ( 0 ; τ ) = η 5 ( τ ) η 2 ( 1 2 τ ) η 2 ( 2 τ ) = η 2 ( 1 2 ( τ + 1 ) ) η ( τ + 1 ) , θ 4 ( 0 , q ) = ϑ 01 ( 0 ; τ ) = η 2 ( 1 2 τ ) η ( τ ) , {\displaystyle {\begin{aligned}\theta _{2}(0,q)=\vartheta _{10}(0;\tau )&={\frac {2\eta ^{2}(2\tau )}{\eta (\tau )}},\\[3pt]\theta _{3}(0,q)=\vartheta _{00}(0;\tau )&={\frac {\eta ^{5}(\tau )}{\eta ^{2}\left({\frac {1}{2}}\tau \right)\eta ^{2}(2\tau )}}={\frac {\eta ^{2}\left({\frac {1}{2}}(\tau +1)\right)}{\eta (\tau +1)}},\\[3pt]\theta _{4}(0,q)=\vartheta _{01}(0;\tau )&={\frac {\eta ^{2}\left({\frac {1}{2}}\tau \right)}{\eta (\tau )}},\end{aligned}}} и
θ 2 ( 0 , q ) θ 3 ( 0 , q ) θ 4 ( 0 , q ) = 2 η 3 ( τ ) . {\displaystyle \theta _{2}(0,q)\,\theta _{3}(0,q)\,\theta _{4}(0,q)=2\eta ^{3}(\tau ).} См. также статью о модулярных функциях Вебера .
J-инвариант равен
k ( τ ) = ϑ 10 ( 0 , τ ) 2 ϑ 00 ( 0 , τ ) 2 {\displaystyle k(\tau )={\frac {\vartheta _{10}(0,\tau )^{2}}{\vartheta _{00}(0,\tau )^{2}}}} а дополнительный эллиптический модуль равен
k ′ ( τ ) = ϑ 01 ( 0 , τ ) 2 ϑ 00 ( 0 , τ ) 2 {\displaystyle k'(\tau )={\frac {\vartheta _{01}(0,\tau )^{2}}{\vartheta _{00}(0,\tau )^{2}}}} Тета-функция Якоби является фундаментальным решением одномерного уравнения теплопроводности с пространственными периодическими граничными условиями[5] z = x {\displaystyle z=x} τ = i t {\displaystyle \tau =it} t , мы можем записать
ϑ ( x , i t ) = 1 + 2 ∑ n = 1 ∞ exp ( − π n 2 t ) cos ( 2 π n x ) {\displaystyle \vartheta (x,it)=1+2\sum _{n=1}^{\infty }\exp \left(-\pi n^{2}t\right)\cos(2\pi nx)} что решает уравнение теплопроводности
∂ ∂ t ϑ ( x , i t ) = 1 4 π ∂ 2 ∂ x 2 ϑ ( x , i t ) . {\displaystyle {\frac {\partial }{\partial t}}\vartheta (x,it)={\frac {1}{4\pi }}{\frac {\partial ^{2}}{\partial x^{2}}}\vartheta (x,it).} Это решение в виде тета-функции является 1-периодическим по x , и при t → 0 {\displaystyle t\to 0} дельта-функции или гребню Дирака в смысле распределений
lim t → 0 ϑ ( x , i t ) = ∑ n = − ∞ ∞ δ ( x − n ) {\displaystyle \lim _{t\rightarrow 0}\vartheta (x,it)=\sum _{n=-\infty }^{\infty }\delta (x-n)} Общие решения для задачи с пространственными периодическими начальными значениями для уравнения теплопроводности могут быть получены путём свёртки начальных данных в t = 0 {\displaystyle t=0}
Тета-функция Якоби является инвариантом при действии дискретной подгруппы группы Гейзенберга . Эта инвариантность представлена в статье о тета-представлении [en]
Если F является квадратичной формой от n переменных, то тета-функция, связанная с F , равна
θ F ( z ) = ∑ m ∈ Z n e 2 π i z F ( m ) {\displaystyle \theta _{F}(z)=\sum _{m\in \mathbb {Z} ^{n}}e^{2\pi izF(m)}} с суммой по решётке целых чисел ℤ n модулярной формой с весом n 2 {\displaystyle {\tfrac {n}{2}}} модулярной группы . В разложении в ряд Фурье
θ ^ F ( z ) = ∑ k = 0 ∞ R F ( k ) e 2 π i k z , {\displaystyle {\hat {\theta }}_{F}(z)=\sum _{k=0}^{\infty }R_{F}(k)e^{2\pi ikz},} числа R F ( k ) {\displaystyle R_{F}(k)} числами представления формы.
Пусть
H n = { F ∈ M ( n , C ) | F = F T , Im F > 0 } {\displaystyle \mathbb {H} _{n}=\left\{F\in M(n,\mathbb {C} )\,{\big |}\,F=F^{\mathsf {T}}\,,\,\operatorname {Im} F>0\right\}} является множеством симметричных квадратных матриц , мнимая часть которых положительно определена . ℍ n верхним полупространством Зигеля [en] верхней полуплоскости . n -Мерным аналогом модулярной группы является симплектическая группа Sp(2n ,ℤ ) . Для n = 1 S p ( 2 , Z ) = S L ( 2 , Z ) {\displaystyle n=1~~~\mathrm {Sp} (2,\mathbb {Z} )=\mathrm {SL} (2,\mathbb {Z} )} n -мерного аналога конгруэнтных подгрупп играет
ker { Sp ( 2 n , Z ) → Sp ( 2 n , Z / k Z ) } . {\displaystyle \ker {\big \{}\operatorname {Sp} (2n,\mathbb {Z} )\rightarrow \operatorname {Sp} (2n,\mathbb {Z} /k\mathbb {Z} ){\big \}}.} Тогда, если дано τ ∈ H n {\displaystyle \tau \in \mathbb {H} _{n}} тета-функция Римана определяется как
θ ( z , τ ) = ∑ m ∈ Z n exp ( 2 π i ( 1 2 m T τ m + m T z ) ) . {\displaystyle \theta (z,\tau )=\sum _{m\in \mathbb {Z} ^{n}}\exp {\bigg (}2\pi i\left({\tfrac {1}{2}}m^{\mathsf {T}}\tau m+m^{\mathsf {T}}z\right){\bigg )}.} Здесь z ∈ C n {\displaystyle z\in \mathbb {C} _{n}} n -мерным комплексным вектором, а верхний индекс T означает транспонирование . Тета-функция Якоби является тогда частным случаем с n = 1 {\displaystyle n=1} τ ∈ H {\displaystyle \tau \in \mathbb {H} } H {\displaystyle \mathbb {H} } верхней полуплоскостью .
Тета-функция Римана сходится абсолютно и равномерно на компактных подмножествах C n × H n {\displaystyle \mathbb {C} ^{n}\times \mathbb {H} _{n}}
Функциональное уравнение функции
θ ( z + a + τ b , τ ) = exp 2 π i ( − b T z − 1 2 b T τ b ) θ ( z , τ ) {\displaystyle \theta (z+a+\tau b,\tau )=\exp 2\pi i\left(-b^{\mathsf {T}}z-{\tfrac {1}{2}}b^{\mathsf {T}}\tau b\right)\theta (z,\tau )} которое выполняется для всех векторов a , b ∈ Z n {\displaystyle a,b\in \mathbb {Z} ^{n}} z ∈ C n {\displaystyle z\in \mathbb {C} ^{n}} τ ∈ H n {\displaystyle \tau \in \mathbb {H} _{n}}
Ряд Пуанкаре [en] автоморфные формы применительно к произвольным фуксовым группам .
Согласно Теореме Абеля-Руффини общее уравнение пятой степени не может быть решено в элементарной радикальной форме. Но общее решение вполне возможно с помощью эллиптических функций. С тета-функцией общий случай Уравнения пятой степени также может быть решен как функция эллиптического «номена q» из эллиптического модуля, который всегда «элементарен» в зависимости от коэффициентов. Для следующего уравнения пятой степени в форме Бринга-Джеррарда общее решение может быть представлено в упрощенной форме тета-функцией ϑ₀₀:
x 5 + 5 x = 4 c {\displaystyle x^{5}+5\,x=4\,c} Для всех реальных значений c {\displaystyle c} x {\displaystyle x} c {\displaystyle c} x {\displaystyle x} c {\displaystyle c}
Método de resolución de las ecuaciones quínticas a través de la función theta Уравнение Бринга – Джеррарда: x 5 + 5 x = 4 c {\displaystyle x^{5}+5\,x=4\,c}
Значение эллиптической функции «Номен q»: Q = q [ ( 2 c 2 + 2 + 2 c 4 + 1 ) − 1 / 2 ( c 4 + 1 + 1 + c ) ] {\displaystyle Q=q{\bigl [}{\bigl (}2c^{2}+2+2{\sqrt {c^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {c^{4}+1}}+1}}+c{\bigr )}{\bigr ]}}
Актуальное решение для x {\displaystyle x} x = [ ϑ 00 ( Q 1 / 5 ) 2 − 5 ϑ 00 ( Q 5 ) 2 ] ϑ 00 ( Q 1 / 5 ) 2 + 5 ϑ 00 ( Q 5 ) 2 − 4 ϑ 00 ( Q ) 2 − 2 ϑ 00 ( Q 1 / 5 ) ϑ 00 ( Q 5 ) 4 ϑ 10 ( Q ) ϑ 01 ( Q ) ϑ 00 ( Q ) {\displaystyle x={\frac {{\bigl [}\vartheta _{00}(Q^{1/5})^{2}-5\,\vartheta _{00}(Q^{5})^{2}{\bigr ]}{\sqrt {\vartheta _{00}(Q^{1/5})^{2}+5\,\vartheta _{00}(Q^{5})^{2}-4\,\vartheta _{00}(Q)^{2}-2\,\vartheta _{00}(Q^{1/5})\,\vartheta _{00}(Q^{5})}}}{4\,\vartheta _{10}(Q)\,\vartheta _{01}(Q)\,\vartheta _{00}(Q)}}}
Ниже в качестве примеров рассматриваются три уравнения, которые можно решить с помощью тета-функции Якоби, но вообще нельзя решить с помощью элементарных корневых выражений:
x 5 + 5 x = 1 3 7 4 {\displaystyle x^{5}+5\,x={\frac {1}{{\sqrt {3}}\,{\sqrt[{4}]{7}}}}} Q = q [ ( 2 c 2 + 2 + 2 c 4 + 1 ) − 1 / 2 ( c 4 + 1 + 1 + c ) ] ( c = 1 4 3 7 4 ) = q ( 3 4 ) = exp [ − π K ( 1 4 7 ) / K ( 3 4 ) ] {\displaystyle Q=q{\bigl [}{\bigl (}2c^{2}+2+2{\sqrt {c^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {c^{4}+1}}+1}}+c{\bigr )}{\bigr ]}{\bigl (}c={\frac {1}{4\,{\sqrt {3}}\,{\sqrt[{4}]{7}}}}{\bigr )}=q{\bigl (}{\frac {3}{4}}{\bigr )}=\exp {\bigl [}-\pi \,K{\bigl (}{\frac {1}{4}}{\sqrt {7}}{\bigr )}/K{\bigl (}{\frac {3}{4}}{\bigr )}{\bigr ]}} Q ≈ 0.0514850134086884874259334407034142264 {\displaystyle Q\approx 0.0514850134086884874259334407034142264} x = { ϑ 00 [ q ( 3 4 ) 1 / 5 ] 2 − 5 ϑ 00 [ q ( 3 4 ) 5 ] 2 } ϑ 00 [ q ( 3 4 ) 1 / 5 ] 2 + 5 ϑ 00 [ q ( 3 4 ) 5 ] 2 − 4 ϑ 00 [ q ( 3 4 ) ] 2 − 2 ϑ 00 [ q ( 3 4 ) 1 / 5 ] ϑ 00 [ q ( 3 4 ) 5 ] 4 ϑ 10 [ q ( 3 4 ) ] ϑ 01 [ q ( 3 4 ) ] ϑ 00 [ q ( 3 4 ) ] {\displaystyle x={\frac {{\bigl \{}\vartheta _{00}[q({\tfrac {3}{4}})^{1/5}]^{2}-5\,\vartheta _{00}[q({\tfrac {3}{4}})^{5}]^{2}{\bigr \}}{\sqrt {\vartheta _{00}[q({\tfrac {3}{4}})^{1/5}]^{2}+5\,\vartheta _{00}[q({\tfrac {3}{4}})^{5}]^{2}-4\,\vartheta _{00}[q({\tfrac {3}{4}})]^{2}-2\,\vartheta _{00}[q({\tfrac {3}{4}})^{1/5}]\,\vartheta _{00}[q({\tfrac {3}{4}})^{5}]}}}{4\,\vartheta _{10}[q({\tfrac {3}{4}})]\,\vartheta _{01}[q({\tfrac {3}{4}})]\,\vartheta _{00}[q({\tfrac {3}{4}})]}}} x ≈ 0.07098926054715586207235133755965679 {\displaystyle x\approx 0.07098926054715586207235133755965679} Тот же образец процедуры применяется в следующем уравнении:
x 5 + 5 x = 17 2 7 15 4 {\displaystyle x^{5}+5\,x={\frac {17}{2\,{\sqrt {7}}\,{\sqrt[{4}]{15}}}}} Q = q [ ( 2 c 2 + 2 + 2 c 4 + 1 ) − 1 / 2 ( c 4 + 1 + 1 + c ) ] ( c = 17 8 7 15 4 ) = q ( 7 8 ) = exp [ − π K ( 1 8 15 ) / K ( 7 8 ) ] {\displaystyle Q=q{\bigl [}{\bigl (}2c^{2}+2+2{\sqrt {c^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {c^{4}+1}}+1}}+c{\bigr )}{\bigr ]}{\bigl (}c={\frac {17}{8\,{\sqrt {7}}\,{\sqrt[{4}]{15}}}}{\bigr )}=q{\bigl (}{\frac {7}{8}}{\bigr )}=\exp {\bigl [}-\pi \,K{\bigl (}{\frac {1}{8}}{\sqrt {15}}{\bigr )}/K{\bigl (}{\frac {7}{8}}{\bigr )}{\bigr ]}} Q ≈ 0.0897074766759280367958684244396699245 {\displaystyle Q\approx 0.0897074766759280367958684244396699245} x = { ϑ 00 [ q ( 7 8 ) 1 / 5 ] 2 − 5 ϑ 00 [ q ( 7 8 ) 5 ] 2 } ϑ 00 [ q ( 7 8 ) 1 / 5
 Из Википедии, бесплатной энциклопедии
Из Википедии, бесплатной энциклопедии
















![{\displaystyle {\begin{aligned}\vartheta _{01}(z;\tau )&=\vartheta \!\left(z+{\tfrac {1}{2}};\tau \right)\\[3pt]\vartheta _{10}(z;\tau )&=\exp \left({\tfrac {1}{4}}\pi i\tau +\pi iz\right)\vartheta \left(z+{\tfrac {1}{2}}\tau ;\tau \right)\\[3pt]\vartheta _{11}(z;\tau )&=\exp \left({\tfrac {1}{4}}\pi i\tau +\pi i\left(z+{\tfrac {1}{2}}\right)\right)\vartheta \left(z+{\tfrac {1}{2}}\tau +{\tfrac {1}{2}};\tau \right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cb2997db68ed0c1efa463393856811997d4e439)





![{\displaystyle \vartheta _{00}{\bigl [}q(k){\bigr ]}={\sqrt {2\pi ^{-1}K(k)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b4faad2fb35cf666dc5b117f38021ea76474437)
![{\displaystyle \vartheta _{01}{\bigl [}q(k){\bigr ]}={\sqrt[{4}]{1-k^{2}}}{\sqrt {2\pi ^{-1}K(k)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd2c4437d76a78a5d6ce5a6a4f3fa7c0daedaab9)
![{\displaystyle \vartheta _{10}{\bigl [}q(k){\bigr ]}={\sqrt {|k|}}{\sqrt {2\pi ^{-1}K(k)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c76189364fb87713c4933622ebf5aee003ae1041)
![{\displaystyle q(k)=\exp {\bigl [}-\pi \,K({\sqrt {1-k^{2}}})/K(k){\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/978283243e43813943c583766e9a5f212208587c)













![{\displaystyle {\begin{aligned}\vartheta _{00}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=\alpha \,\vartheta _{00}(z;\tau )\quad &\vartheta _{01}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=\alpha \,\vartheta _{10}(z;\tau )\\[3pt]\vartheta _{10}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=\alpha \,\vartheta _{01}(z;\tau )\quad &\vartheta _{11}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=-i\alpha \,\vartheta _{11}(z;\tau ).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e38521d263e968c6643113cb856744c3d8417638)


![{\displaystyle {\begin{aligned}\vartheta _{00}(w,q)&=\sum _{n=-\infty }^{\infty }(w^{2})^{n}q^{n^{2}}\quad &\vartheta _{01}(w,q)&=\sum _{n=-\infty }^{\infty }(-1)^{n}(w^{2})^{n}q^{n^{2}}\\[3pt]\vartheta _{10}(w,q)&=\sum _{n=-\infty }^{\infty }(w^{2})^{n+{\frac {1}{2}}}q^{\left(n+{\frac {1}{2}}\right)^{2}}\quad &\vartheta _{11}(w,q)&=i\sum _{n=-\infty }^{\infty }(-1)^{n}(w^{2})^{n+{\frac {1}{2}}}q^{\left(n+{\frac {1}{2}}\right)^{2}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db65827472877657a7aa66887c63a13ecd71483a)










![{\displaystyle {\begin{aligned}\vartheta _{01}(z\mid q)&=\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1-2\cos(2\pi z)q^{2m-1}+q^{4m-2}\right),\\[3pt]\vartheta _{10}(z\mid q)&=2q^{\frac {1}{4}}\cos(\pi z)\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+2\cos(2\pi z)q^{2m}+q^{4m}\right),\\[3pt]\vartheta _{11}(z\mid q)&=-2q^{\frac {1}{4}}\sin(\pi z)\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1-2\cos(2\pi z)q^{2m}+q^{4m}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a2f486ca65bf1df31851e9591220ff601cf6fb0)
![{\displaystyle {\begin{aligned}\vartheta _{00}(z;\tau )&=-i\int _{i-\infty }^{i+\infty }{e^{i\pi \tau u^{2}}{\frac {\cos(2uz+\pi u)}{\sin(\pi u)}}}\mathrm {d} u;\\[6pt]\vartheta _{01}(z;\tau )&=-i\int _{i-\infty }^{i+\infty }{e^{i\pi \tau u^{2}}{\frac {\cos(2uz)}{\sin(\pi u)}}}\mathrm {d} u;\\[6pt]\vartheta _{10}(z;\tau )&=-ie^{iz+{\frac {1}{4}}i\pi \tau }\int _{i-\infty }^{i+\infty }{e^{i\pi \tau u^{2}}{\frac {\cos(2uz+\pi u+\pi \tau u)}{\sin(\pi u)}}}\mathrm {d} u;\\[6pt]\vartheta _{11}(z;\tau )&=e^{iz+{\frac {1}{4}}i\pi \tau }\int _{i-\infty }^{i+\infty }{e^{i\pi \tau u^{2}}{\frac {\cos(2uz+\pi \tau u)}{\sin(\pi u)}}}\mathrm {d} u.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d64804e9cd7ac2b0dbe01eb172d0eaeb0289601a)


![{\displaystyle \vartheta _{10}(e^{-\pi x})=\theta _{2}(0;e^{-\pi x})=\sum _{n=-\infty }^{\infty }\exp {\bigl [}-\pi x(n+{\tfrac {1}{2}})^{2}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56cbe03235f9d5c944f94de4bf301172bf36018b)

![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-1/4}={\sqrt {G}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b5806ac256d4f9cbee2e600b107b796149525d2)
![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}=2^{1/4}{\sqrt {G}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/275164859145587e57e6dcec09ff6a14acdb50a5)

![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-3/4}{\sqrt {{\sqrt {2}}-1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e434be718ca9f45eab55f4be6dbc809f452b143e)
![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-3/4}{\sqrt {{\sqrt {2}}+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/811f3b7a90a5c68d52be4b97dc0baa54896b6b34)

![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-3/2}3^{-3/8}{\sqrt {{\sqrt {3}}-1}}({\sqrt {3}}+1-{\sqrt[{4}]{12}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/274ab98328bf81360ae485dd6c4ec3876c0b1677)
![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-1/4}3^{-3/8}{\sqrt {{\sqrt {3}}+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e503d680361cd99abd6c5f17e2484532ec5c7cf)

![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/4}({\sqrt[{4}]{2}}-1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9da6f4b51282acd6cdbb1f4f000e147120becd7)
![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/4}({\sqrt[{4}]{2}}+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7e896b6a925a2e195d345679b8775787f9b92a2)

![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/4}5^{-1/2}({\sqrt[{4}]{5}}-1)^{2}\Phi ^{-1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8941a32268dba27298e7fab0251b49ef306927f0)
![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}5^{-1/2}\Phi ^{3/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62eae1843959ef981d29f3c7b929bd157cdaa3f5)
![{\displaystyle \vartheta _{00}({\text{e}}^{-6\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-2}3^{-3/8}{\sqrt {\cot({\tfrac {1}{24}}\pi )}}({\sqrt[{4}]{3}}+1)({\sqrt {3}}+1-{\sqrt[{4}]{12}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb035a3d45e2ab6f147fe0bec8d206162c2a15a0)
![{\displaystyle \vartheta _{00}({\text{e}}^{-7\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/8}7^{-7/16}{\sqrt[{4}]{3+{\sqrt {7}}}}{\sqrt {5-{\sqrt {7}}+{\sqrt[{4}]{28}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/079109c07c2dd02b4822f57cae3d61bb0d7cf3cf)
![{\displaystyle \vartheta _{00}({\text{e}}^{-8\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-2}({\sqrt {2+{\sqrt {2}}}}+2^{7/8})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc00f43c5679fce7a316e3bdef61c4d133592207)
![{\displaystyle \vartheta _{00}({\text{e}}^{-9\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}3^{-1}({\sqrt[{3}]{2{\sqrt {3}}+2}}+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2f877403163382ad95f8da98d21b4d2fc205092)
![{\displaystyle \vartheta _{00}({\text{e}}^{-10\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}5^{-1/2}\Phi ^{3/2}\cos {\bigl [}{\tfrac {1}{4}}\arcsin {\bigl (}\Phi ^{-12}{\bigr )}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0756934d88de0d3a5d8008ead1b12d77476f501d)
![{\displaystyle \vartheta _{00}({\text{e}}^{-11\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/4}11^{-5/8}{\sqrt {{\sqrt {11}}+3}}\,{\bigl \{}4+{\sqrt {11}}-3{\sqrt {3}}\tanh {\bigl [}{\tfrac {1}{4}}\operatorname {arcosh} ({\tfrac {7}{4}})+{\tfrac {1}{2}}\operatorname {artanh} ({\tfrac {4}{9}}{\sqrt {3}})-{\tfrac {1}{6}}\operatorname {artanh} ({\tfrac {1}{27}}{\sqrt {3}}){\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb81295f05f9079f715931c7109b1d0979be3d)
![{\displaystyle \vartheta _{00}({\text{e}}^{-12\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-2}3^{-3/8}{\sqrt {\cot({\tfrac {1}{24}}\pi )}}({\sqrt[{4}]{3}}+1)({\sqrt {3}}+1-{\sqrt[{4}]{12}})\cos {\bigl \{}{\tfrac {1}{2}}\arcsin {\bigl [}{\tfrac {1}{2}}(2+{\sqrt {3}})({\sqrt {3}}-{\sqrt {2}})^{2}({\sqrt {2}}-1)^{2}({\sqrt[{4}]{3}}-1)^{4}{\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3535d0f5aff637d7fa1f5fb731bda1ca56232042)
![{\displaystyle \vartheta _{00}({\text{e}}^{-13\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}13^{-1/2}{\sqrt {5{\sqrt {13}}+18}}\,{\bigl \{}{\tfrac {1}{6}}(5{\sqrt {39}}-17{\sqrt {3}})\coth {\bigl [}{\tfrac {1}{3}}\operatorname {artanh} ({\tfrac {6}{11}}{\sqrt {3}})-{\tfrac {1}{2}}\operatorname {arcosh} {\bigl (}{\tfrac {4}{13}}{\sqrt {13}}{\bigr )}{\bigr ]}-{\tfrac {1}{2}}({\sqrt {13}}-3){\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffbc8bbd8eb051776538f7399d9241cc7bad6994)
![{\displaystyle \vartheta _{00}({\text{e}}^{-14\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/8}7^{-7/16}{\sqrt[{4}]{3+{\sqrt {7}}}}{\sqrt {5-{\sqrt {7}}+{\sqrt[{4}]{28}}}}\,\cos {\bigl \{}{\tfrac {1}{4}}\arcsin {\bigl [}({\tfrac {1}{4}}{\sqrt {14}}+{\tfrac {1}{4}}{\sqrt {2}}-{\tfrac {1}{2}}{\sqrt[{4}]{7}})^{12}{\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de4c6ae2063c452fd09f57285b304c98b262873a)
![{\displaystyle \vartheta _{00}({\text{e}}^{-15\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}3^{-1/2}5^{-1/2}\Phi ^{3/2}{\bigl (}{\sqrt {2{\sqrt {1+\Phi ^{-8}+\Phi ^{-16}}}+2+\Phi ^{-8}}}+{\sqrt {1-\Phi ^{-8}}}{\bigr )}^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e8482d7ff471533dd3dd6c13b6e1350a97e1c79)
![{\displaystyle \vartheta _{00}({\text{e}}^{-16\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}{\bigl [}2^{-9/4}({\sqrt[{4}]{2}}+1)+2^{-23/16}{\sqrt[{4}]{{\sqrt {2}}+1}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c9e004698837d0e5da1653e6e8a2bd3ffd907e9)
![{\displaystyle \vartheta _{00}({\text{e}}^{-17\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-3/2}17^{-1/2}{\bigl [}({\sqrt[{4}]{17}}+1){\sqrt {{\sqrt {17}}-1}}+{\sqrt[{8}]{272}}{\sqrt {{\sqrt {17}}+3}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bd0fe0c9e9a2064182136c689f2c5fe7d7e3a89)
![{\displaystyle \vartheta _{00}({\text{e}}^{-18\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}3^{-1}({\sqrt[{3}]{2{\sqrt {3}}+2}}+1)\cos {\bigl \langle }{\tfrac {1}{4}}\arcsin {\bigl \{}{\bigl [}2{\sqrt {3}}-3-{\sqrt {6}}(2-{\sqrt {3}})^{5/6}+{\sqrt {2}}(2-{\sqrt {3}})^{7/6}{\bigr ]}^{4}{\bigr \}}{\bigr \rangle }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/833c183d94b8f58204f266fe5054cf8ebf71adef)


![{\displaystyle \vartheta _{00}[\exp(-{\tfrac {1}{2}}\pi )]={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-1/4}{\sqrt {{\sqrt {2}}+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6aef9793232d82700431269f0815b5196af0e44)
![{\displaystyle \vartheta _{00}[\exp(-{\tfrac {1}{3}}\pi )]={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-1/4}3^{1/8}{\sqrt {{\sqrt {3}}+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dee33b151e0a465dae4144dcc937f2f7ab5227cd)
![{\displaystyle \vartheta _{00}[\exp(-\pi /y)]={\sqrt {y}}\,\vartheta _{00}[\exp(-\pi y)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae9008aff5514d5f893a3af0c31690ed0e2840dd)
![{\displaystyle \vartheta _{00}[\exp(-{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-1/6}3^{-1/8}\beta ({\tfrac {1}{3}})^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ab6074806527425e7de1c3ebbf6fbabfb430f11)
![{\displaystyle \vartheta _{00}[\exp(-2{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-1/6}3^{-1/8}\beta ({\tfrac {1}{3}})^{1/2}\cos({\tfrac {1}{24}}\pi )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9ff9967dce3b0989b6ab4ae153b98767a3a08c5)
![{\displaystyle \vartheta _{00}[\exp(-3{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-1/6}3^{-7/8}\beta ({\tfrac {1}{3}})^{1/2}({\sqrt[{3}]{2}}+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e1b28ec514bb28b4a21769d27dc53eda142872d)
![{\displaystyle \vartheta _{00}[\exp(-4{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-7/6}3^{-1/8}\beta ({\tfrac {1}{3}})^{1/2}[1+{\sqrt {\cos({\tfrac {1}{12}}\pi )}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7d1a15726742041d3cbd480d532593d3a4d4516)
![{\displaystyle \vartheta _{00}[\exp(-5{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-1/6}3^{-9/8}\beta ({\tfrac {1}{3}})^{1/2}\sin({\tfrac {1}{5}}\pi )({\tfrac {2}{5}}{\sqrt[{3}]{100}}+{\tfrac {2}{5}}{\sqrt[{3}]{10}}+{\tfrac {3}{5}}{\sqrt {5}}+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0f741bdad21e8b749424137653d6029be72b216)
![{\displaystyle \vartheta _{01}[\exp(-{\sqrt {2}}\,\pi )]=2^{-1/4}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1aff2b55af25b0f4add279d206e80df5b5c13ab5)
![{\displaystyle \vartheta _{01}[\exp(-3{\sqrt {2}}\,\pi )]=2^{-1/4}3^{-1/2}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}\,{\sqrt {{\sqrt {3}}+{\sqrt {2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fe479485ffb9796f403a3fccf34b952f4ebf71e)
![{\displaystyle \vartheta _{01}[\exp(-{\tfrac {1}{3}}{\sqrt {2}}\,\pi )]=2^{-1/4}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}\,{\sqrt {{\sqrt {3}}-{\sqrt {2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4aa898e7dd5333f54c63b488daeb68feff8dde9)
![{\displaystyle \vartheta _{01}[\exp(-5{\sqrt {2}}\,\pi )]=2^{-1/4}5^{-1/2}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}\,{\bigl \{}{\tfrac {4}{3}}{\sqrt {2}}\cos({\tfrac {1}{10}}\pi )\cosh[{\tfrac {1}{3}}\operatorname {artanh} ({\tfrac {3}{8}}{\sqrt {6}})]+{\tfrac {1}{3}}\tan({\tfrac {1}{5}}\pi ){\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb4e1e51392a27416293df642c7d659bcf01d33f)
![{\displaystyle \vartheta _{01}[\exp(-{\tfrac {1}{5}}{\sqrt {2}}\,\pi )]=2^{-1/4}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}\,{\bigl \{}{\tfrac {4}{3}}{\sqrt {2}}\sin({\tfrac {1}{5}}\pi )\cosh[{\tfrac {1}{3}}\operatorname {artanh} ({\tfrac {3}{8}}{\sqrt {6}})]-{\tfrac {1}{3}}\cot({\tfrac {1}{10}}\pi ){\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/800bd571aa0a2533b4a64b5f270c12c5156b458d)
![{\displaystyle {\begin{aligned}\vartheta _{4}^{2}(q)&=iq^{\frac {1}{4}}\sum _{k=-\infty }^{\infty }q^{2k^{2}-k}\vartheta _{1}\left({\frac {2k-1}{2i}}\ln q,q\right),\\[6pt]\vartheta _{4}^{2}(q)&=\sum _{k=-\infty }^{\infty }q^{2k^{2}}\vartheta _{4}\left({\frac {k\ln q}{i}},q\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8c16f39ab9443e220062eaad77d207fd8ff5cb0)
![{\displaystyle {\begin{aligned}{\sqrt {\frac {\pi {\sqrt {e^{\pi }}}}{2}}}\cdot {\frac {1}{\Gamma ^{2}\left({\frac {3}{4}}\right)}}&=i\sum _{k=-\infty }^{\infty }e^{\pi \left(k-2k^{2}\right)}\vartheta _{1}\left({\frac {i\pi }{2}}(2k-1),e^{-\pi }\right),\\[6pt]{\sqrt {\frac {\pi }{2}}}\cdot {\frac {1}{\Gamma ^{2}\left({\frac {3}{4}}\right)}}&=\sum _{k=-\infty }^{\infty }{\frac {\vartheta _{4}\left(ik\pi ,e^{-\pi }\right)}{e^{2\pi k^{2}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e539c4d92a7653e109301a20da7afb6e1325a1f)
![{\displaystyle {\begin{aligned}\vartheta (z,\tau )=\vartheta _{3}(z,\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau +{\frac {1}{2}}+{\frac {\tau }{2}}\\[3pt]\vartheta _{1}(z,\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau \\[3pt]\vartheta _{2}(z,\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau +{\frac {1}{2}}\\[3pt]\vartheta _{4}(z,\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau +{\frac {\tau }{2}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0a46570a37094335d8daa1755155d36ad316b6d)





![{\displaystyle {\begin{aligned}\theta _{2}(0,q)=\vartheta _{10}(0;\tau )&={\frac {2\eta ^{2}(2\tau )}{\eta (\tau )}},\\[3pt]\theta _{3}(0,q)=\vartheta _{00}(0;\tau )&={\frac {\eta ^{5}(\tau )}{\eta ^{2}\left({\frac {1}{2}}\tau \right)\eta ^{2}(2\tau )}}={\frac {\eta ^{2}\left({\frac {1}{2}}(\tau +1)\right)}{\eta (\tau +1)}},\\[3pt]\theta _{4}(0,q)=\vartheta _{01}(0;\tau )&={\frac {\eta ^{2}\left({\frac {1}{2}}\tau \right)}{\eta (\tau )}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51aa288fda023bcc1b7d82366605089d3abd4800)






























![{\displaystyle Q=q{\bigl [}{\bigl (}2c^{2}+2+2{\sqrt {c^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {c^{4}+1}}+1}}+c{\bigr )}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4792b84301ec4aae6064d082c060afe68e927ded)
![{\displaystyle x={\frac {{\bigl [}\vartheta _{00}(Q^{1/5})^{2}-5\,\vartheta _{00}(Q^{5})^{2}{\bigr ]}{\sqrt {\vartheta _{00}(Q^{1/5})^{2}+5\,\vartheta _{00}(Q^{5})^{2}-4\,\vartheta _{00}(Q)^{2}-2\,\vartheta _{00}(Q^{1/5})\,\vartheta _{00}(Q^{5})}}}{4\,\vartheta _{10}(Q)\,\vartheta _{01}(Q)\,\vartheta _{00}(Q)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bfa954d820b6bcc9a441b962c15b6259e3ac23f)
![{\displaystyle x^{5}+5\,x={\frac {1}{{\sqrt {3}}\,{\sqrt[{4}]{7}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e807db5d61e4e2cd6480d7059e7322058e44ec73)
![{\displaystyle Q=q{\bigl [}{\bigl (}2c^{2}+2+2{\sqrt {c^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {c^{4}+1}}+1}}+c{\bigr )}{\bigr ]}{\bigl (}c={\frac {1}{4\,{\sqrt {3}}\,{\sqrt[{4}]{7}}}}{\bigr )}=q{\bigl (}{\frac {3}{4}}{\bigr )}=\exp {\bigl [}-\pi \,K{\bigl (}{\frac {1}{4}}{\sqrt {7}}{\bigr )}/K{\bigl (}{\frac {3}{4}}{\bigr )}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9027a2ec761653e2128a33bf3dbc17fa6bd3272b)

![{\displaystyle x={\frac {{\bigl \{}\vartheta _{00}[q({\tfrac {3}{4}})^{1/5}]^{2}-5\,\vartheta _{00}[q({\tfrac {3}{4}})^{5}]^{2}{\bigr \}}{\sqrt {\vartheta _{00}[q({\tfrac {3}{4}})^{1/5}]^{2}+5\,\vartheta _{00}[q({\tfrac {3}{4}})^{5}]^{2}-4\,\vartheta _{00}[q({\tfrac {3}{4}})]^{2}-2\,\vartheta _{00}[q({\tfrac {3}{4}})^{1/5}]\,\vartheta _{00}[q({\tfrac {3}{4}})^{5}]}}}{4\,\vartheta _{10}[q({\tfrac {3}{4}})]\,\vartheta _{01}[q({\tfrac {3}{4}})]\,\vartheta _{00}[q({\tfrac {3}{4}})]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bafd4b4dac43e7f79b26845badb00a8a2745e13)

![{\displaystyle x^{5}+5\,x={\frac {17}{2\,{\sqrt {7}}\,{\sqrt[{4}]{15}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d664c424b51a6bf071f170b832827c1ad75dc8c)
![{\displaystyle Q=q{\bigl [}{\bigl (}2c^{2}+2+2{\sqrt {c^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {c^{4}+1}}+1}}+c{\bigr )}{\bigr ]}{\bigl (}c={\frac {17}{8\,{\sqrt {7}}\,{\sqrt[{4}]{15}}}}{\bigr )}=q{\bigl (}{\frac {7}{8}}{\bigr )}=\exp {\bigl [}-\pi \,K{\bigl (}{\frac {1}{8}}{\sqrt {15}}{\bigr )}/K{\bigl (}{\frac {7}{8}}{\bigr )}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1e615531310bdc1f0cfc6e1537486ac0a5f9bb4)
