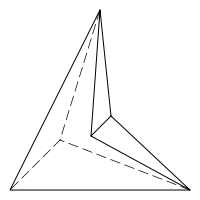
Hexaeder

Hexaeder [hɛksaˈeːdər], von griech. ἑξάεδρον hexáedron, „Sechsflächner“, bezeichnet allgemein ein Polyeder mit sechs ebenen Begrenzungsflächen. Dabei handelt es sich im Allgemeinen nicht um einen regulären platonischen Vielflächner, sondern einen beliebigen von sechs ebenen Flächen begrenzten Körper. Im Speziellen, insbesondere im Zusammenhang mit platonischen Körpern, handelt es sich um das regelmäßige Hexaeder bzw. den Würfel mit den 6 kongruenten Flächen.

Unterscheidet man nach der Struktur (genauer: nach dem zugrundeliegenden Kantengraphen, so dass z. B. ein Parallelepiped und ein Pyramidenstumpf mit vierseitiger Grundfläche nicht von einem Würfel zu unterscheiden, dagegen all diese hingegen von einer Pyramide mit fünfeckiger Grundfläche), so gibt es nur sieben graphentheoretisch verschiedene Typen konvexer Hexaeder^[1]:

Flächen: 4, 4, 4, 4, 4, 4 Kanten: 12,  Ecken: 8	Flächen: 5,  3, 3, 3, 3, 3 Kanten: 10,  Ecken: 6	Flächen: 5,  4, 4,  3, 3, 3 Kanten: 11,  Ecken: 7	Flächen: 5, 5,  4, 4,  3, 3 Kanten: 12,  Ecken: 8
Würfel, Quader, Parallelepiped, Rhomboeder, Trigonales Trapezo­eder, Pyramiden­stumpf mit vier­eckiger Grund- und Deckfläche	Pyramide mit fünfeckiger Grundfläche
Flächen: 3, 3, 3, 3, 3, 3 Kanten: 9,  Ecken: 5	Flächen: 4, 4, 4, 4,  3, 3 Kanten: 11,  Ecken: 7	Flächen: 4, 4,  3, 3, 3, 3 Kanten: 10,  Ecken: 6
Doppeltetraeder		Dieser Körper weist Chiralität auf: Es gibt eine „linkshändige“ und eine „rechtshändige“ Variante, die durch Ebenenspiegelung auseinander hervorgehen.

Betrachtet man auch nichtkonvexe Hexaeder, so kommen noch die folgenden drei Typen mit „Auskerbung“ dazu:

Flächen: 4, 4,  3, 3, 3, 3 Kanten: 10,  Ecken: 6	Flächen: 5, 5,  3, 3, 3, 3 Kanten: 11,  Ecken: 7	Flächen: 6, 6,  3, 3, 3, 3 Kanten: 12,  Ecken: 8

Vom Würfel-Typ (6 Flächen, 12 Kanten, 8 Ecken) gibt es folgende Formen:

Grafik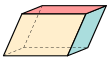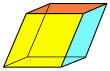
Name	Würfel	Quader	Trigonal trapezohedron	Trigonal trapezohedron	Quadrilateral Kegelstumpf	Parallelepiped	Rhombohedron
Flächen	Quadrat	drei Paare von Rechtecken	kongruente Rhomben	kongruente Vierecke	quadratischer Pyramidenstumpf	drei Paare von Parallelogrammen	drei Paare von Rhomben
Symmetrien	Oh, [4,3], (*432) order 48 (8 Spiegelungen, 3! Achspermutationen)	D2h, [2,2], (*222) order 8 (8 Spiegelungen, wenn alle Achsen unterschiedlich lang)	D3d, [2+,6], (2*3) order 12	D3, [2,3]+, (223) order 6	C4v, [4], (*44) order 8	Ci, [2+,2+], (×) order 2

• Eine organische Verbindung, die wie ein Würfel aufgebaut ist, ist das nach dem englischen Cube (englisch für Würfel) benannte Cuban.
• Kubische Kristallsysteme kommen bei der Beschreibung des geometrischen Aufbaus von Kristallen vor, wie zum Beispiel beim Kochsalz (Natriumchlorid-Struktur).

• Würfel
• Platonischer Körper

• Abgeschrägtes Hexaeder

• Beweis zur Existenz von genau sieben konvexen Hexaedern: Anatole Beck, Michael Bleicher, Donald Crowe: Excursions into Mathematics. 1969, S. 29–30. 

Commons: Hexaeder – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Hexaeder – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

1. ↑ Martin Gardner: Denkspiele von anderen Planeten. Hugendubel, München 1986, ISBN 3-88034-295-4, S. 134.