دستهبندی آماری

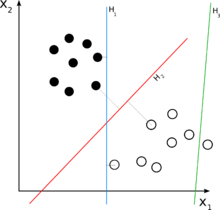
یادگیری ماشینی و آمار، ردهبندی[۱] (به انگلیسی: Classification)، دستهبندی یا طبقهبندی مسئلهٔ شناسایی تعلق یک مشاهده جدید به کدام یک از مجموعه دستهها (زیر-جمعیتها)، بر اساس یک مجموعه از دادههای مورد استفاده به منظور آموزش شامل مشاهدات است که عضویت در دستههایشان معلوم است.[۲] در اصطلاح یادگیری ماشین، طبقهبندی نوعی یادگیری با نظارت است، که مجموعهای دادهها برای آموزش موجودند. برای نمونه طبقهبندی ایمیلها به اسپم و غیراسپم یک طبقهبندی با دو دسته است. اگر الگوریتمی بخواهد ایمیلهای دریافتشده را طبقهبندی کند هر ایمیل به کلاس اسپم یا غیراسپم تعلق خواهد داشت. این نمونهای از یک طبقهبندی دودویی است.[۳] در مقابل طبقهبندی دودویی، طبقهبندی چندکلاسه قرار دارد (برای نمونه تشخیص یک عدد بین ۰ تا ۹ از روی تصویر نه کلاس دارد). طبقهبندیهای چندکلاسه معمولاً دشوارتر از طبقهبندی دودویی هستند.[۳][۴]
الگوریتمی که طبقهبندی را اجرا میکند، بهویژه در یک پیادهسازی بتن، بهعنوان یک طبقهبندی شناخته میشود. اصطلاح «طبقهبند» گاهی به تابع ریاضی پیادهسازی شده توسط یک الگوریتم طبقهبندی نیز اشاره دارد که دادههای ورودی را به یک دسته نگاشت میکند.
اصطلاحات در زمینهها کاملاً متنوع است. در آمار، جایی که طبقهبندی اغلب با رگرسیون لجستیک یا رویههای مشابه انجام میشود، ویژگیهای مشاهدات را متغیرهای توضیحی (یا متغیرهای مستقل، رگرسیونها و غیره) مینامند، و دستههایی که باید پیشبینی شوند بهعنوان پیامدها شناخته میشوند که بهعنوان مقادیر ممکن متغیر وابسته باشد، در نظر گرفته میشوند. در یادگیری ماشینی، مشاهدات اغلب بهعنوان نمونه شناخته میشوند. متغیرهای توضیحی ویژگیها نامیده میشوند (در یک بردار ویژگی گروهبندی میشوند)، و دستههای احتمالی قابل پیشبینی کلاسها هستند. سایر زمینهها ممکن است از اصطلاحات مختلفی استفاده کنند: بهعنوان مثال در بومشناسی جامعه، اصطلاح «طبقهبندی» معمولاً به تجزیه و تحلیل خوشهای اشاره دارد.
ارتباط با مشکلات دیگر
[ویرایش]طبقهبندی و خوشهبندی نمونههایی از مشکل کلیتر تشخیص الگو هستند که تخصیص نوعی مقدار خروجی به یک مقدار ورودی دادهشدهاست. نمونههای دیگر رگرسیون هستند که یک خروجی با ارزش واقعی به هر ورودی اختصاص میدهد. برچسب گذاری توالی که به هر عضو یک دنباله از مقادیر یک کلاس اختصاص میدهد (بهعنوان مثال، بخشی از برچسب زدن گفتار، که بخشی از گفتار را به هر کلمه در یک جمله ورودی اختصاص میدهد). تجزیه که درخت تجزیه را به یک جملهٔ ورودی اختصاص میدهد و ساختار نحوی جمله را توصیف میکند؛ و غیره.
یک زیر کلاس رایج طبقهبندی، طبقهبندی احتمالی است. الگوریتمهایی با این ماهیت از استنتاج آماری برای یافتن بهترین کلاس برای یک نمونه معین استفاده میکنند. بر خلاف سایر الگوریتمها، که به سادگی یک کلاس «بهترین» را ارائه میدهند، الگوریتمهای احتمالی احتمال عضوی از هر یک از کلاسهای ممکن را بهدست میآورند. بهترین کلاس معمولاً بهعنوان کلاس با بالاترین احتمال انتخاب میشود. با این حال، چنین الگوریتمی مزایای متعددی نسبت به طبقهبندیکنندههای غیراحتمالی دارد:
- میتواند یک مقدار اطمینان مرتبط با انتخاب خود را خروجی دهد (بهطور کلی، طبقهبندیکنندهای که بتواند این کار را انجام دهد بهعنوان طبقهبندیکننده با وزن اطمینان شناخته میشود).
- به همین ترتیب، زمانی که اعتمادش به انتخاب یک خروجی خاص خیلی کم باشد، میتواند خودداری کند.
- به دلیل احتمالات ایجادشده، طبقهبندیکنندههای احتمالی را میتوان بهطور مؤثرتری در وظایف بزرگتر یادگیری ماشینی گنجاند، به گونهای که تا حدی یا بهطور کامل از مشکل انتشار خطا جلوگیری کرد.
رویههای مکرر
[ویرایش]کار اولیه بر روی طبقهبندی آماری توسط فیشر انجام شد،[۵][۶] در زمینهٔ مسائل دو گروهی، که منجر به تابع تفکیک خطی فیشر بهعنوان قاعدهای برای اختصاص یک گروه به یک مشاهدهٔ جدید شد.[۷] در این کار اولیه فرض شد که مقادیر داده در هر یک از دو گروه دارای یک توزیع نرمال چندمتغیره است. گسترش همین زمینه به بیش از دو گروه نیز با محدودیتی که قاعدهٔ طبقهبندی باید خطی باشد در نظر گرفته شدهاست.[۷][۸] کار بعدی برای توزیع نرمال چندمتغیره باعث شد طبقهبندیکننده غیرخطی باشد:[۹] چندین قانون طبقهبندی را میتوان بر اساس تنظیمات مختلف فاصله ماهالانوبیس استخراج کرد، با مشاهدهٔ جدیدی که به گروهی که مرکز آن کمترین فاصلهٔ تنظیمشده را با مشاهده دارد، اختصاص داد.
رویههای بیزی
[ویرایش]بر خلاف رویههای مکرر، روشهای طبقهبندی بیزی روشی طبیعی برای در نظر گرفتن هرگونه اطلاعات موجود دربارهٔ اندازههای نسبی گروههای مختلف در کل جمعیت ارائه میکند.[۱۰] رویههای بیزی از نظر محاسباتی گران هستند و در روزهای قبل از توسعهٔ محاسبات زنجیرهای مارکوف مونت کارلو، تقریبیهایی برای قوانین خوشهبندی بیزی ابداع شد.[۱۱]
برخی از رویههای بیزی شامل محاسبهٔ احتمال عضویت در گروه میشوند: این روشها نتیجهٔ آموزندهتری را نسبت به نسبت دادن سادهٔ یک برچسب گروهی به هر مشاهدهٔ جدید ارائه میدهند.
طبقهبندی دودویی و چندکلاسه
[ویرایش]طبقهبندی را میتوان بهعنوان دو مشکل جداگانه در نظر گرفت. طبقهبندی باینری و طبقهبندی چندطبقه. در طبقهبندی باینری، وظیفهای که بهتر درک میشود، فقط دو کلاس درگیر هستند، در حالی که طبقهبندی چندکلاسه شامل تخصیص یک شیء به یکی از چندین کلاس است. از آنجایی که بسیاری از روشهای طبقهبندی بهطور خاص برای طبقهبندی باینری توسعه یافتهاند، طبقهبندی چندکلاسه اغلب به استفادهٔ ترکیبی از طبقهبندیکنندههای دودویی متعدد نیاز دارد.
بردارهای ویژگی
[ویرایش]بیشتر الگوریتمها یک نمونه منفرد را توصیف میکنند که دستهٔ آن باید با استفاده از بردار ویژگی ویژگیهای فردی و قابل اندازهگیری نمونه پیشبینی شود. هر خصوصیت یک ویژگی نامیده میشود که در آمار بهعنوان یک متغیر توضیحی نیز شناخته میشود (یا متغیر مستقل، اگرچه ویژگیها ممکن است از نظر آماری مستقل باشند یا نباشند). ویژگیها ممکن است باینری باشند (بهعنوان مثال «روشن» یا «خاموش»). طبقهبندیشده (مثلاً «A»، «B»، «AB» یا «O»، برای گروه خونی)، ترتیبی (مثلاً «بزرگ»، «متوسط» یا «کوچک»)، با مقدار صحیح (مثلاً تعداد تکرار یک کلمهٔ خاص در ایمیل) یا با ارزش واقعی (مثلاً اندازهگیری فشار خون). اگر نمونه یک تصویر باشد، مقادیر ویژگی ممکن است با پیکسلهای یک تصویر مطابقت داشته باشد. اگر نمونه یک قطعه متن باشد، مقادیر ویژگی ممکن است فراوانی وقوع کلمات مختلف باشد. برخی از الگوریتمها فقط بر حسب دادههای گسسته کار میکنند و نیاز دارند که دادههای با ارزش واقعی یا با مقدار صحیح به گروههایی گسسته شوند (مثلاً کمتر از ۵، بین ۵ تا ۱۰، یا بیشتر از ۱۰).
طبقهبندیکنندههای خطی
[ویرایش]تعداد زیادی از الگوریتمها برای طبقهبندی را میتوان در قالب یک تابع خطی بیان کرد که با ترکیب بردار ویژگی یک نمونه با بردار وزنها، با استفاده از حاصل ضرب نقطهای، به هر دستهٔ ممکن k امتیازی اختصاص میدهد. دستهبندی پیشبینیشده، دستهای است که بالاترین امتیاز را دارد. این نوع از تابع امتیاز بهعنوان یک تابع پیشبینی خطی شناخته میشود و دارای شکل کلی زیر است:
که در آن Xi بردار ویژگی برای مثال i است ، βk بردار وزنهای مربوط به دستهٔ k است، و امتیاز (Xi , k) امتیاز مربوط به اختصاص مثال i به دستهٔ k است. در تئوری انتخاب گسسته، جایی که نمونهها نشاندهندهٔ افراد و دستهها نشاندهنده انتخابها هستند، امتیاز بهعنوان ابزاری در نظر گرفته میشود که با فردی که دستهٔ k را انتخاب میکند، مرتبط است.
الگوریتمهایی با این تنظیمات اولیه بهعنوان طبقهبندیکنندهٔ خطی شناخته میشوند. آنچه آنها را متمایز میکند، روش تعیین (آموزش) وزنها/ضرایب بهینه و نحوهٔ تفسیر امتیاز است.
نمونههایی از این الگوریتمها:
- رگرسیون لجستیک و رگرسیون لجستیک چندجملهای
- رگرسیون پروبیت
- الگوریتم پرسپترون
- ماشینهای بردار پشتیبانی میکند
- تجزیه و تحلیل تفکیک خطی.
الگوریتمها
[ویرایش]از آنجایی که هیچ شکل واحدی از طبقهبندی برای همهٔ مجموعهٔ دادهها مناسب نیست، مجموعهٔ ابزار بزرگی از الگوریتمهای طبقهبندی توسعه داده شدهاست. متداولترین آنها عبارتند از:[۱۲]
- طبقهبندیکنندههای خطی
- ماشینهای بردار پشتیبانی
- طبقهبندیکنندههای درجهٔ دوم
- تخمین کرنل
- تقویت (فرا الگوریتم)
- درخت تصمیم
- شبکههای عصبی
- برنامهریزی ژنتیکی
- آموزش کوانتیزاسیون برداری
ارزیابی
[ویرایش]عملکرد طبقهبندیکننده تا حد زیادی به ویژگیهای دادههایی که باید طبقهبندی شوند بستگی دارد. هیچ طبقهبندیکنندهای وجود ندارد که در تمام مسائل دادهشده به بهترین شکل کار کند (پدیدهای که ممکن است با قضیهٔ بدون ناهار رایگان توضیح داده شود). تستهای تجربی مختلفی برای مقایسهٔ عملکرد طبقهبندیکننده و یافتن ویژگیهای دادههایی که عملکرد طبقهبندیکننده را تعیین میکنند، انجام شدهاست. با این حال، تعیین طبقهبندیکنندهٔ مناسب برای یک مسئلهٔ معین، بیشتر یک هنر است تا یک علم.
دقت اندازهگیری و یادآوری معیارهای رایجی هستند که برای ارزیابی کیفیت یک سیستم طبقهبندی استفاده میشوند. اخیراً، منحنیهای مشخصهٔ عملکرد گیرنده (ROC) برای ارزیابی مبادلهٔ بین نرخهای مثبت درست و نادرست الگوریتمهای طبقهبندی استفاده شدهاند.
بهعنوان یک معیار عملکرد، ضریب عدم قطعیت مزیتی نسبت به دقت ساده دارد، زیرا تحت تأثیر اندازههای نسبی کلاسهای مختلف قرار نمیگیرد.[۱۳] علاوه بر این، الگوریتمی را برای تنظیم مجدد کلاسها جریمه نمیکند.
دامنههای کاربردی
[ویرایش]طبقهبندی کاربردهای زیادی دارد. در برخی از آنها بهعنوان یک روش دادهکاوی استفاده میشود، در حالی که در برخی دیگر مدلسازی آماری دقیقتری انجام میشود.
- بینایی کامپیوتر
- تصویربرداری پزشکی و تجزیه و تحلیل تصویر پزشکی
- تشخیص نوری کاراکتر
- ردیابی ویدیو
- کشف و توسعهٔ دارو
- زمینآمار
- تشخیص گفتار
- تشخیص دستخط
- شناسایی زیستسنجی
- طبقهبندی بیولوژیکی
- پردازش زبان طبیعی آماری
- طبقهبندی اسناد
- موتورهای جستجوی اینترنتی
- امتیازدهی اعتباری
- تشخیص الگو
- سیستم توصیهگر
- طبقهبندی میکرو آرایه
جستارهای وابسته
[ویرایش]- هوش مصنوعی
- طبقهبندی دودویی
- طبقهبندی احتمالی
- قوانین طبقهبندی
- پردازش مدت مرکب
- انبار داده
- دادهکاوی
- پایگاه داده تحلیلی
- منطق فازی
- بازیابی اطلاعات
- فهرست مجموعههای داده برای تحقیقات یادگیری ماشین
- یادگیری ماشینی
- سامانه توصیهگر
منابع
[ویرایش]- ↑ «ردهبندی دادهها» [رایانه و فنّاوری اطلاعات] همارزِ «data classification»؛ منبع: گروه واژهگزینی. جواد میرشکاری، ویراستار. دفتر دوم. فرهنگ واژههای مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۶۴-۷۵۳۱-۳۷-۰ (ذیل سرواژهٔ ردهبندی دادهها)
- ↑ T. Hastie, R. Tibshirani, and J. Friedman, “The Elements of Statistical Learning,” Bayesian Forecast. Dyn. Model. , vol. 1, pp. 1–694, 2009.
- ↑ ۳٫۰ ۳٫۱ Provost, F. , & Fawcett, T. (2013). Data Science for Business: What you need to know about data mining and data-analytic thinking. " O'Reilly Media, Inc.".
- ↑ Piryonesi S. Madeh; El-Diraby Tamer E. (2020-06-01). "Role of Data Analytics in Infrastructure Asset Management: Overcoming Data Size and Quality Problems". Journal of Transportation Engineering, Part B: Pavements. 146 (2): 04020022. doi:10.1061/JPEODX.0000175.
- ↑ Fisher, R. A. (1936). "The Use of Multiple Measurements in Taxonomic Problems". Annals of Eugenics. 7 (2): 179–188. doi:10.1111/j.1469-1809.1936.tb02137.x.
{{cite journal}}:|hdl-access=requires|hdl=(help) - ↑ Fisher, R. A. (1938). "The Statistical Utilization of Multiple Measurements". Annals of Eugenics. 8 (4): 376–386. doi:10.1111/j.1469-1809.1938.tb02189.x.
{{cite journal}}:|hdl-access=requires|hdl=(help) - ↑ ۷٫۰ ۷٫۱ Gnanadesikan, R. (1977) Methods for Statistical Data Analysis of Multivariate Observations, Wiley. شابک ۰−۴۷۱−۳۰۸۴۵−۵ (p. 83–86)
- ↑ Rao, C.R. (1952) Advanced Statistical Methods in Multivariate Analysis, Wiley. (Section 9c)
- ↑ Anderson, T.W. (1958) An Introduction to Multivariate Statistical Analysis, Wiley.
- ↑ Binder, D. A. (1978). "Bayesian cluster analysis". Biometrika. 65: 31–38. doi:10.1093/biomet/65.1.31.
- ↑ Binder, David A. (1981). "Approximations to Bayesian clustering rules". Biometrika. 68: 275–285. doi:10.1093/biomet/68.1.275.
- ↑ "A Tour of The Top 10 Algorithms for Machine Learning Newbies". Built In. 2018-01-20. Retrieved 2019-06-10.
- ↑ Peter Mills (2011). "Efficient statistical classification of satellite measurements". International Journal of Remote Sensing. 32 (21): 6109–6132. arXiv:1202.2194. Bibcode:2011IJRS...32.6109M. doi:10.1080/01431161.2010.507795.
