Distorsion (optique)

Pour les articles homonymes, voir Distorsion.

En optique la distorsion est une aberration géométrique apparaissant quand les conditions menant à l'approximation de Gauss ne sont plus respectées. La distorsion se manifeste le plus visiblement sur les lignes droites : une grille imagée par un système à forte distorsion aura une forme dite en « barillet », la grille est bombée vers l'extérieur, ou en « coussinet », la grille image ayant l'air déformée vers l'intérieur.

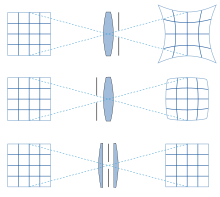
La distorsion est une aberration géométrique de champ ou d'inclinaison^[1]. Les aberrations géométriques apparaissent lorsque l'on s'éloigne des conditions de Gauss, là où les aberrations chromatiques apparaissent lorsque l'on ne travaille plus avec une lumière monochromatique. Les aberrations de champ sont les aberrations dépendantes de la position du point objet dans le champ^[2].

Le principe de la distorsion est que deux points objets B₁ et B₂, situés à des distances différentes d₁ et d₂ de l'axe optique, traversent le système optique en des endroits différents et sont donc focalisés différemment en B'₁ et B'₂^[2]. Ce défaut est principalement dû à la variation du grandissement transversal en fonction de la distance à l'axe dans la combinaison optique^[3].

La distorsion est proportionnelle à d³, le cube de la distance du point objet à l'axe optique. Cette aberration est donc indépendante de la dimension de la pupille^[4] et de l'inclinaison du rayon par rapport à l'axe^[5].

Dans le système des aberrations de Seidel, les aberrations dépendent des coordonnées x, y du rayon incident dans la pupille, et de X et Y, les positions en abscisses et ordonnées du point image. Étant donné que les systèmes étudiés dans le domaine des aberrations de Seidel sont centrés et de révolution il est possible de simplifier les variables et l'aberration du front d'onde s'écrit ${\displaystyle W(x^{2}+y^{2},yY,Y^{2})}$ et un développement limité amène^[6] :

${\displaystyle {\begin{aligned}W(x^{2}+y^{2},yY,Y^{2})\simeq &W_{0}+\\&a_{1}(x^{2}+y^{2})+a_{2}yY+a_{3}Y^{2}+\\&b_{1}(x^{2}+y^{2})^{2}+b_{2}(x^{2}+y^{2})yY+b_{3}y^{2}Y^{2}+b_{4}(x^{2}+y^{2})Y^{2}+b_{5}yY^{3}+b_{6}Y^{4}+\cdots \end{aligned}}}$

Des simplifications sont possibles dans cette expression, qui ne touchent pas le terme ${\displaystyle b_{5}yY^{3}}$ qui définit la distorsion. Ce terme montre, que pour deux points B₁ et B₂ où Y₁<Y₂ alors δY₁<δY₂, et une grille sera déformée en forme de coussinet si b₅ est négatif, en forme de barillet s'il est positif^[7].

Cette aberration d'ordre trois peut cohabiter avec son équivalent d'ordre 5. En effet, une distorsion en barillet d'ordre 3 avec une distorsion en coussinet d'ordre 5 donne ce que l'on appelle de la « distorsion en moustache ».

• 
  Distorsion en barillet, aberration d'ordre trois dans les polynômes de Seidel.
• 
  Distorsion en coussinet, aberration d'ordre trois dans les polynômes de Seidel.
• 
  Distorsion en moustache, aberration d'ordre trois compensée par une aberration d'ordre cinq dans les polynômes de Seidel.

Le magazine Chasseur d'Images qui teste les objectifs photographiques considère comme^{[réf. souhaitée]} :

• négligeable une distorsion (positive ou négative) de moins de 0,3 % ;
• peu sensible une distorsion de 0,3 % ou 0,4 % ;
• sensible une distorsion de 0,5 % ou 0,6 % ;
• très sensible une distorsion de 0,7 % à 0,9 % ;
• gênante une distorsion de 1 % ou plus.

Un système sans distorsion est dit orthoscopique ou rectilinéaire^[3].

Le principe de symétrie peut s'énoncer comme suit :

« Lorsqu'un système optique possède une symétrie exacte par rapport à sa pupille ou son diaphragme, le système sera non entaché de coma, de distorsion et de chromatisme latéral. »

— Smith 1992, p. 39

Ce principe découle de l'annulation des aberrations citées, les aberrations positives d'un côté ont leur équivalent négatif de l'autre, donnant une combinaison optique dont les aberrations s'équilibrent et s'annulent. Ce principe n'est que théorique car il implique que le système travaille à grandissement unité, avec objet et image à distances égales, en plus de posséder une formule optique exactement identique des deux côtés du diaphragme avec des verres identiques^[8].

La plupart des combinaisons optiques corrigeant correctement la distorsion ne cherchent donc qu'à approcher le principe de symétrie^[8].

Un exemple de système dépourvu de distorsion est le sténopé^[9]. Les objectifs rectilinéaires apparaissent vers le milieu du XX^e siècle^[10] grâce des constructions symétriques des combinaisons optiques. Les aplanats ainsi sont montés avec un diaphragme au centre de deux groupes de lentilles dans la combinaison de manière à les rendre rectilinéaires.

L'aplanat de Steinheil est constitué de deux groupes séparés par un diaphragme, chaque groupe constitué d'un doublet collé crown/flint en forme de ménisque. L'inconvénient dans cette combinaison est l'astigmatisme, la distorsion pouvant être éliminée^[10]. Une autre combinaison simple est le triplet de Cooke dont la symétrie approchée grâce à ses deux lentilles extérieures en crown de forme similaires et sa lentille biconcave centrale en flint à laquelle le diaphragme est accolé^[8].

L'objectif dissymétrique de Petzval, inventé en 1840, est aussi composé de deux groupes de lentilles, le groupe avant constitué d'un doublet collé crown/flint, le deuxième groupe constitué d'une lentille convergente, crown, une lentille divergente en flint, non collées^[10].

La présence de distorsion est particulièrement notable dans les objectifs à grand champ comme les objectifs grand angle ou les systèmes de projection^[11]. En outre les combinaisons permettant de scanner une image sont sciemment entachées de distorsion. Là où un système peu aberrant et sans distorsion a une hauteur d'image suivant la loi ${\displaystyle h=f\tan {(\theta )}}$, où h est la hauteur image, f la focale et θ l'angle de champ. Dans ce type de combinaisons optiques, une distorsion négative est introduite afin de transformer la relation en ${\displaystyle h=f\theta }$^[12].

La distorsion en barillet est un défaut caractéristique d'un objectif grand angle. Des distorsions de +0,5 % à +1 % sont courantes avec des objectifs grand angle de focale fixes.^{[réf. souhaitée]} Pour les retrofocus la distorsion provient essentiellement de la position de la pupille, très proche des composants à l'arrière du système : le principe de symétrie est complètement absent, rendant la correction de la distorsion illusoire. Lors des optimisations de ce genre de combinaisons, Warren J. Smith conseille ainsi de relâcher les contraintes sur cette aberration de manière à laisser évoluer la combinaison plus facilement vers des configurations stables^[13].

Sur un objectif fisheye, la distorsion est de l'ordre de +16 %,^{[réf. souhaitée]} quantité considérable mais inévitable étant donné qu'il est nécessaire d'imager un champ de 180° sur une surface plane. Dans ce genre de configurations la distorsion en barillet devient nécessaire pour contrecarrer la perte de flux en bord de champ. Les fisheye peuvent subir, à cause de leur angle extrême, les conséquences de la distorsion chromatique, c'est-à-dire la variation de la loi de distorsion avec la longueur d'onde^[14].

Un autre système optique, l'oculaire, est typiquement très entaché de distorsion. La conception d'un oculaire de télescope ou de microscope nécessite en général de positionner le diaphragme proche ou au niveau de l'objectif et la pupille de sortie, là où doit se placer l’œil, est en dehors de la combinaison, parfois de 10 à 20 mm au-delà de l'oculaire. Le principe de symétrie n'étant pas respecté, la distorsion est donc très présente^[15]. Une distorsion de plusieurs pour-cents, parfois de 8 à 12 % pour des oculaires grand-angles sont des valeurs répandues. La qualité image hors d'axe de ce type de systèmes est souvent médiocre, mais l’œil opérant lui aussi assez mal hors d'axe, ces défauts sont souvent considérés comme tolérables^[15]. Dans des oculaires plus complexes, à 4 lentilles, on peut retrouver le principe de symétrie. Les oculaires orthoscopiques, dits symétriques ou oculaires Ploessl, permettent souvent une distance œil-oculaire confortable et grande^[16].

En photographie numérique, deux modes de correction de la distorsion sont disponibles.

Le premier mode est une correction intégrée à l'appareil qui à partir des informations EXIF (comportant le modèle d'objectif utilisé, la focale de prise de vue et éventuellement la distance du sujet) introduit, à partir d'une base de données ou de données fournies par l'objectif lui-même, la correction adéquate^[17]. Le principal obstacle est qu'il est impératif d'utiliser pour cela (du moins pour les appareils à objectif interchangeable) un objectif répertorié donc, généralement, un modèle fabriqué par le constructeur de l'appareil. Cette correction amène un léger recadrage de l'image si bien que la fonction de correction de la distorsion est normalement désactivable pour les cas où ce recadrage est gênant.^{[réf. nécessaire]}

Ouvrages en français utilisés pour la rédaction de l'article :

• Richard Taillet, Pascal Febvre et Loïc Villain, Dictionnaire de physique, De Boeck, coll. « De Boeck Supérieur », novembre 2009, 754 p.
• Bernard Balland, Optique géométrique : imagerie et instruments, Lausanne, Presses polytechniques et universitaires romandes, 2007, 1^re éd., 860 p. (ISBN 978-2-88074-689-6, lire en ligne), p. 335

Ouvrages en langue étrangère utilisés pour la rédaction de l'article :

• (en) Warren J. Smith, Modern Lens Design : A resource manual, New York/St Louis/San Francisco, McGraw-Hill, coll. « Optical and electro-optical engineering », 1992, 473 p. (ISBN 0-07-059178-4)

• Optique géométrique
• Objectif grand angle
• Objectif fisheye
• Objectif de longue focale
• Zoom
• Objectif macro

• Portail de l’optique
• Portail de la photographie