List of isotoxal polyhedra and tilings

In geometry, isotoxal polyhedra and tilings are defined by the property that they have symmetries taking any edge to any other edge.^[1] Polyhedra with this property can also be called "edge-transitive", but they should be distinguished from edge-transitive graphs, where the symmetries are combinatorial rather than geometric.

Regular polyhedra are isohedral (face-transitive), isogonal (vertex-transitive), and isotoxal (edge-transitive).

Quasiregular polyhedra are isogonal and isotoxal, but not isohedral; their duals are isohedral and isotoxal, but not isogonal.

The dual of an isotoxal polyhedron is also an isotoxal polyhedron. (See the Dual polyhedron article.)

The dual of a convex polyhedron is also a convex polyhedron.^[2]

There are nine convex isotoxal polyhedra based on the Platonic solids: the five (regular) Platonic solids, the two (quasiregular) common cores of dual Platonic solids, and their two duals.

The vertex figures of the quasiregular forms are (squares or) rectangles; the vertex figures of the duals of the quasiregular forms are (equilateral triangles and equilateral triangles, or) equilateral triangles and squares, or equilateral triangles and regular pentagons.

Form	Regular	Dual regular	Quasiregular	Quasiregular dual
Wythoff symbol	q | 2 p	p | 2 q	2 | p q
Vertex configuration	pq	qp	p.q.p.q
p=3 q=3	Tetrahedron {3,3} 3 | 2 3	Tetrahedron {3,3} 3 | 2 3	Tetratetrahedron (Octahedron) 2 | 3 3	Cube (Rhombic hexahedron)
p=4 q=3	Cube {4,3} 3 | 2 4	Octahedron {3,4} 4 | 2 3	Cuboctahedron 2 | 3 4	Rhombic dodecahedron
p=5 q=3	Dodecahedron {5,3} 3 | 2 5	Icosahedron {3,5} 5 | 2 3	Icosidodecahedron 2 | 3 5	Rhombic triacontahedron

The dual of a non-convex polyhedron is also a non-convex polyhedron.^[2] (By contraposition.)

There are ten non-convex isotoxal polyhedra based on the quasiregular octahedron, cuboctahedron, and icosidodecahedron: the five (quasiregular) hemipolyhedra based on the quasiregular octahedron, cuboctahedron, and icosidodecahedron, and their five (infinite) duals:

Form	Quasiregular	Quasiregular dual
p=3 q=3	Tetrahemihexahedron	Tetrahemihexacron
p=4 q=3	Cubohemioctahedron	Hexahemioctacron
	Octahemioctahedron	Octahemioctacron (visually indistinct from Hexahemioctacron) (*)
p=5 q=3	Small icosihemidodecahedron	Small icosihemidodecacron (visually indistinct from Small dodecahemidodecacron) (*)
	Small dodecahemidodecahedron	Small dodecahemidodecacron

(*) Faces, edges, and intersection points are the same; only, some other of these intersection points, not at infinity, are considered as vertices.

There are sixteen non-convex isotoxal polyhedra based on the Kepler–Poinsot polyhedra: the four (regular) Kepler–Poinsot polyhedra, the six (quasiregular) common cores of dual Kepler–Poinsot polyhedra (including four hemipolyhedra), and their six duals (including four (infinite) hemipolyhedron-duals):

Form	Regular	Dual regular	Quasiregular	Quasiregular dual
Wythoff symbol	q | 2 p	p | 2 q	2 | p q
Vertex configuration	pq	qp	p.q.p.q
p=5/2 q=3	Great stellated dodecahedron {5/2,3} 3 | 2 5/2	Great icosahedron {3,5/2} 5/2 | 2 3	Great icosidodecahedron   2 | 3 5/2	Great rhombic triacontahedron
			Great icosihemidodecahedron	Great icosihemidodecacron
			Great dodecahemidodecahedron	Great dodecahemidodecacron
p=5/2 q=5	Small stellated dodecahedron {5/2,5} 5 | 2 5/2	Great dodecahedron {5,5/2} 5/2 | 2 5	Dodecadodecahedron   2 | 5 5/2	Medial rhombic triacontahedron
			Small icosihemidodecahedron	Small dodecahemicosacron
			Great dodecahemidodecahedron	Great dodecahemicosacron

Finally, there are six other non-convex isotoxal polyhedra: the three quasiregular ditrigonal (3 | p q) star polyhedra, and their three duals:

Quasiregular	Quasiregular dual
3 | p q
Great ditrigonal icosidodecahedron 3/2 | 3 5	Great triambic icosahedron
Ditrigonal dodecadodecahedron 3 | 5/3 5	Medial triambic icosahedron
Small ditrigonal icosidodecahedron 3 | 5/2 3	Small triambic icosahedron

There are at least 5 polygonal tilings of the Euclidean plane that are isotoxal. (The self-dual square tiling recreates itself in all four forms.)

Regular	Dual regular	Quasiregular	Quasiregular dual
Hexagonal tiling {6,3} 6 | 2 3	Triangular tiling {3,6} 3 | 2 3	Trihexagonal tiling 2 | 3 6	Rhombille tiling
Square tiling {4,4} 4 | 2 4	Square tiling {4,4} 2 | 4 4	Square tiling {4,4} 4 | 2 4	Square tiling {4,4}

There are infinitely many isotoxal polygonal tilings of the hyperbolic plane, including the Wythoff constructions from the regular hyperbolic tilings {p,q}, and non-right (p q r) groups.

Here are six (p q 2) families, each with two regular forms, and one quasiregular form. All have rhombic duals of the quasiregular form, but only one is shown:

[p,q]	{p,q}	{q,p}	r{p,q}	Dual r{p,q}
Coxeter-Dynkin
[7,3]	{7,3}	{3,7}	r{7,3}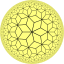
[8,3]	{8,3}	{3,8}	r{8,3}
[5,4]	{5,4}	{4,5}	r{5,4}
[6,4]	{6,4}	{4,6}	r{6,4}
[8,4]	{8,4}	{4,8}	r{8,3}
[5,5]	{5,5}	{5,5}	r{5,5}

Here's 3 example (p q r) families, each with 3 quasiregular forms. The duals are not shown, but have isotoxal hexagonal and octagonal faces.

Coxeter-Dynkin
(4 3 3)	3 | 4 3	3 | 4 3	4 | 3 3
(4 4 3)	4 | 4 3	3 | 4 4	4 | 4 3
(4 4 4)	4 | 4 4	4 | 4 4	4 | 4 4

All isotoxal polyhedra listed above can be made as isotoxal tilings of the sphere.

In addition as spherical tilings, there are two other families which are degenerate as polyhedra. Even ordered hosohedron can be semiregular, alternating two lunes, and thus isotoxal:

• hosohedron {2,q}
• dihedron {p,2}

• Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1. (6.4 Isotoxal tilings, 309–321)
• Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), "Uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 246 (916): 401–450, Bibcode:1954RSPTA.246..401C, doi:10.1098/rsta.1954.0003, ISSN 0080-4614, JSTOR 91532, MR 0062446, S2CID 202575183