クリティカルパス法

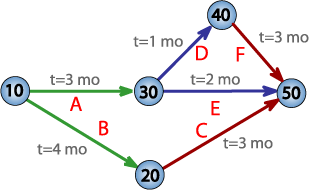
クリティカルパス法（クリティカルパスほう、英: critical path method, CPM）またはクリティカルパス分析（クリティカルパスぶんせき、英: critical path analysis）は、プロジェクトの一連の活動（アクティビティ）をスケジューリングするための数学的アルゴリズムである。効率的プロジェクトマネジメントのための重要なツールである。

CPMは1950年代にデュポン社が開発した。同じ頃、ジェネラル・ダイナミクスとアメリカ海軍が Program Evaluation and Review Technique (PERT) を開発していた^[1]。現在では、ソフトウェア開発、研究プロジェクト、製品開発、工学、プラント保守などといった各種プロジェクトで利用されている。複数の独立した活動から構成される任意のプロジェクトでスケジューリング技法として適用可能である。

CPMを使う際の基本的テクニックは、以下を含むプロジェクトのモデルを構築することである。

1. プロジェクトを完了させるまでに必要な全ての活動の一覧
2. 各活動にかかる時間
3. 活動間の依存関係

これらの値を使い、CPMによってプロジェクト完了までにかかる最長の経路（依存関係のある一連の活動の連なり）を計算し、プロジェクト完了を延期せずにそれぞれの活動をスケジュールした場合の開始と終了の最も早い時期と最も遅い時期を求める。これによって、どの活動が「クリティカル」（すなわち、最長経路上にある）かを決め、どの活動に「トータルフロート」（すなわち、プロジェクトを遅延させずに活動開始を遅延できること）があるかを決める。プロジェクトマネジメントにおいてクリティカルパス（経路）とは、必要な時間を積算したときに最長となる一連の活動を意味する。これによって、プロジェクト完了までにかかる最短時間を決定できる。クリティカルパス上の活動に遅延が生じると、プロジェクト完了予定日に直接的な影響が生じる。すなわち、クリティカルパスにはフロート（余裕時間）が全くない。1つのプロジェクトに複数の並行するクリティカルパスが存在することもある。クリティカルパスと並行していてフロートのある経路は、準クリティカルパス、または非クリティカルパスと呼ぶ。

これらの結果により管理者は活動を優先順位付けでき、プロジェクトの管理を効率化できる。そして、活動群をさらに並行に実施できるようにしたり（ファストトラッキング）、クリティカルパスにさらにリソースを投入して期間を短縮させたりすることで、プロジェクト全体をより早期に完了させることもできる。

本来、クリティカルパス法は各要素の論理的依存関係しか考慮していなかった。その後、各活動に要するリソース量を考慮するよう拡張されていった。これをリソース平準化 (resource leveling) と呼ぶ。リソース平準化されたスケジュールでは、リソースボトルネックによる遅延もありうる（すなわち、必要なときに必要なリソースが使えない）。すると、それまではクリティカルパスでなかった経路が「リソースクリティカル」パスとなることもある。関連する概念としてクリティカルチェーンがある。これは、リソースの制約による予期しない遅延を防ぐための手法である。

一般にプロジェクトのスケジュールは定期的に更新されるので、そのたびにCPMを行って、どの活動がクリティカルかを判断する。例えば、クリティカルでない活動がフロート以上に遅延すると、新たなクリティカルパスが生まれ、プロジェクトに遅延が生じる。さらに、Program Evaluation and Review Technique (PERT) などを使って確率的予測の概念を導入することも容易である。

産業向けにCPM法を使ったスケジューリングを行うソフトウェアがいくつかある。例えば、KPlato、TaskJuggler、Microsoft Project などがある。ただし、クリティカルパス法自体はコンピュータとは無関係に開発された。

クリティカルパス法を使って生成したスケジュールは、その元となる情報が単なる見積もりであるため、正確でないことが多い。1つの間違いでも分析結果に影響を与えることがある。見積もりを盲目的に信じ、変化に素早く対応することを怠ると、プロジェクトに混乱をきたす。しかし、クリティカルパス分析をしておけば、どんな変化が起きても、それによってスケジュールにどういう影響があるかを見極めることができ、素早く対策を打つことができる。例えば、プロジェクトの事後分析の重要な要素である As Built Critical Path (ABCP) では、本来のスケジュールと実際のスケジュールを比較して、どの変化がスケジュールに重大な影響を与えたかを分析する。

グラフ G=G(N,E) を与えられたとき（Nはノード、Eはエッジ）、O記法を使うと、CPMアルゴリズムにかかる時間は O(E) となる。これは各エッジを2回ずつ調べることでグラフの幾何学的順序付けをするのに O(E) を要するからであり、エッジ数に比例した時間がかかる。

出典は列挙するだけでなく、脚注などを用いてどの記述の情報源であるかを明記してください。 記事の信頼性向上にご協力をお願いいたします。（2022年12月）

• Project Management Institute (2003). A Guide To The Project Management Body Of Knowledge (3rd ed.). Project Management Institute. ISBN 1-930699-45-X 
• Klastorin, Ted (2003). Project Management: Tools and Trade-offs (3rd ed.). Wiley. ISBN 978-0471413844 
• Heerkens, Gary (2001). Project Management (The Briefcase Book Series). McGraw-Hill. ISBN 0-07-137952-5 
• Kerzner, Harold (2003). Project Management: A Systems Approach to Planning, Scheduling, and Controlling (8th ed.). ISBN 0-471-22577-0 
• Lewis, James (2002). Fundamentals of Project Management (2nd ed.). American Management Association. ISBN 0-8144-7132-3 
• Lev Virine & Michael Trumper (2007). Project Decisions: The Art and Science. Management Concepts. ISBN 978-1567262179 
• Milosevic, Dragan Z. (2003). Project Management ToolBox: Tools and Techniques for the Practicing Project Manager. Wiley. ISBN 978-0471208228 
• Woolf, Murray B. (2007). Faster Construction Projects with CPM Scheduling. McGraw Hill. ISBN 978-0071486606  Critical Path method

• Program Evaluation and Review Technique
• Work Breakdown Structure
• ガントチャート
• ネットワーク理論
• プロジェクト
• プロジェクトマネジメント
• 動的計画法
• 構造化プログラミング
• センターピン理論

• Critical path web calculator
• A Few Critical Path Articles PM Hut
• A good slide show explaining critical path concepts Slideshare.net
• Critical Path Java Applet