Апейрогон
Из Википедии, бесплатной энциклопедии
Апейрогон или бесконечноугольник (от др.-греч. ἄπειρος — бесконечный или безграничный и др.-греч. γωνία — угол) — обобщённый многоугольник со счётно-бесконечным числом сторон[1].
Правильный апейрогон[править | править код]
Правильный апейрогон имеет стороны равной длины, как и любой другой правильный многоугольник. Его символ Шлефли — {∞}, диаграмма Коксетера — Дынкина — 
.
Правильный апейрогон разбивает плоскость на две полуплоскости, образуя апейрогональный диэдр {∞,2}. Внутренняя часть апейрогона может быть определена путём указания направления сторон.
| Правильные | Однородные | ||
|---|---|---|---|
| ∞.∞ | 2∞ | 4.4.∞ | 3.3.3.∞ |
 |  |  |  |
{∞, 2} | {2, ∞} | t{2, ∞} | sr{2, ∞}  |
Правильными апейрогонами можно считать прямые, состоящие из рёбер четырёх однородных мозаик и пяти мозаик, двойственных однородным, на евклидовой плоскости.
| 3 направления | 1 направление | 2 направления | |
|---|---|---|---|
 Шеститреугольная мозаика |  Треугольный паркет |  Удлинённая треугольная мозаика |  Квадратный паркет (кадриль) |
| 3 направления | 6 направлений | 1 направление | 4 направления | |
|---|---|---|---|---|
 Тетрамозаика |  Разделённая треугольная мозаика |  Разделённая шестиугольная мозаика |  Призматическая пятиугольная мозаика |  Разделённая квадратная мозаика |
Неправильные апейрогоны[править | править код]
Изогональный апейрогон имеет вершины одного типа и чередующиеся стороны двух типов (длин).
Квазиправильный апейрогон — изогональный апейрогон с равными длинами сторон.
Изотоксальный апейрогон является двойственным по отношению к изогональному. Он имеет один тип рёбер и два типа вершин и геометрически идентичен правильному апейрогону, что можно показать чередующейся раскраской вершин в два цвета.
| Правильный | …  … |
|---|---|
| Квазиправильный | …  … |
| Изогональный | …  … |
| Изотоксальный | …  … |
Апейрогоны на плоскости Лобачевского[править | править код]
Правильные апейрогоны на плоскости Лобачевского имеют кривизну, также как и многоугольники с конечным числом сторон. Вокруг апейрогона на плоскости Лобачевского можно описать орицикл или эквидистанту (гиперцикл), аналогично тому, как вокруг многоугольника с конечным числом сторон может быть описана окружность.
| 3 | 4 | 5 |
|---|---|---|
 {∞,3}  |  {∞,4}  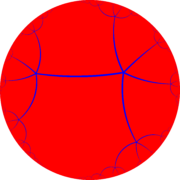|  {∞,5}  |
| 6 | 7 | 8 | … | ∞ |
|---|---|---|---|---|
 {∞,6}  |  {∞,7}  |  {∞,8}  |  {∞,∞} |
| {∞, 3} | tr{∞, 3} | tr{12i, 3} |
|---|---|---|
Правильный: {∞} | 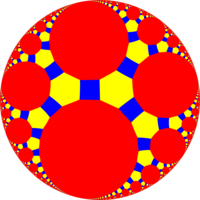 Квазиправильный: t{∞} |  Квазиправильный: t{12i} |
Примечания[править | править код]
- ↑ Coxeter, Regular polytopes, p.45
Литература[править | править код]
- H. S. M. Coxeter. Regular Polytopes. — 3rd. — New York: Dover Publications, 1973. — С. 121–122. — ISBN 0-486-61480-8.
- Grünbaum, B. Regular polyhedra — old and new, Aequationes Math. 16 (1977) p. 1-20
- Coxeter, H. S. M. and Moser, W. O. J. Generators and Relations for Discrete Groups. — New York: Springer-Verlag, 1980. — ISBN 0-387-09212-9. (1st ed, 1957) 5.2 The Petrie polygon {p, q}.
Ссылки[править | править код]
- 'Russell, Robert A.. Apeirogon (англ.) на сайте Wolfram MathWorld.
- Olshevsky, George. Apeirogon. Glossary for Hyperspace. Архивировано 4 февраля 2007 года.
| Многоугольники | |
|---|---|
| Звёздчатые многоугольники | |
| Паркеты на плоскости | |
| Правильные многогранники и сферические паркеты | |
| Многогранники Кеплера — Пуансо | |
| Соты | |
| Четырёхмерные многогранники | |
 | Для улучшения этой статьи желательно:
|