射影作用素

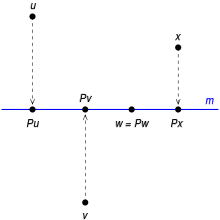
線型代数学および函数解析学における射影作用素あるいは単に射影（しゃえい、英: projection）とは、いわゆる射影（投影）を一般化した概念である。有限次元ベクトル空間 V の場合は、V 上の線型変換 P: V → V であって、冪等律 P² = P を満たすものを言う。ベクトル v の像 Pv を v の射影という。射影作用素はベクトル空間 V を U⊕W と直和分解したときに、V の元 v = u + w (u ∈ U, w ∈ W) を u に写すような変換である。ベクトル空間の次元が無限次元の場合には、連続性を考慮しなければならない。例えばヒルベルト空間 ${\displaystyle {\mathcal {H}}}$ における射影作用素とは、${\displaystyle {\mathcal {H}}}$ 上の有界線型作用素 ${\displaystyle P\in {\mathcal {L}}({\mathcal {H}})}$ であって、冪等律 P² = P を満たすものを言う。このときさらに自己共役性 P^∗ = P を持つときには直交射影（ちょっこうしゃえい、英: orthogonal projection）という^[1]。直交射影のことを単に射影と呼ぶこともある^[2]。

この定義は抽象的ではあるが、投影図法の考え方を一般化し、定式化したものになっている。 幾何学的対象上の射影の影響は、その対象の各点における射影の影響を調べることでわかる。

例えば、三次元空間 R³ の点 (x, y, z) を点 (x, y, 0) へ写す写像は xy-平面の上への射影である。この写像は行列

${\displaystyle P={\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\end{bmatrix}}}$

によって表現される。実際、この行列 P の任意のベクトルへの作用は

${\displaystyle P{\begin{bmatrix}x\\y\\z\end{bmatrix}}={\begin{bmatrix}x\\y\\0\end{bmatrix}}}$

となり、これが射影を定めること（つまり P = P² を満たすこと）は

${\displaystyle P^{2}{\begin{bmatrix}x\\y\\z\end{bmatrix}}=P{\begin{bmatrix}x\\y\\0\end{bmatrix}}={\begin{bmatrix}x\\y\\0\end{bmatrix}}}$

なる計算によって確かめられる。

（定義は後述するが）直交でない（斜交）射影の簡単な例として

${\displaystyle P={\begin{bmatrix}0&0\\\alpha &1\end{bmatrix}}}$

を挙げることができる。行列の積の定義に従って計算すれば

${\displaystyle P^{2}={\begin{bmatrix}0&0\\\alpha &1\end{bmatrix}}{\begin{bmatrix}0&0\\\alpha &1\end{bmatrix}}={\begin{bmatrix}0&0\\\alpha &1\end{bmatrix}}=P}$

故に P が実際に射影となることが分かる。

この射影 P が直交射影となるのは α = 0 のときであり、かつそのときに限る。

以下、本節において考えるベクトル空間はすべて有限次元であるものと仮定する（この場合、射影の連続性などを気にしなくともすむ）。

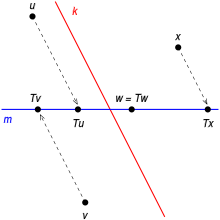
本項冒頭の導入文で述べたとおり、射影 P は冪等律すなわち P² = P を満たすような線型変換である。

もととなるベクトル空間を W とする。W の部分線型空間 U および V が、それぞれ P の値域および零空間（核）であるものと仮定すると、基本的な性質として

• P は U 上に恒等作用素 I として作用する。つまり、
  ${\displaystyle \forall x\in U,\quad Px=x.}$
• 直和分解 W = U ⊕ V が成立する。すなわち、W の各ベクトル x は U の元 u と V の元 v を用いて x = u + v なる形に一意的に表される。これには
  ${\displaystyle u=Px,\quad v=x-Px=(I-P)x}$
  とすればよい。

などが成り立つことがわかる。射影の値域と核は互いに「相補的」なもので、P と Q = I − P も同じく「相補的」である。すなわち、作用素 Q もやはり射影を定め、Q の値域は P の核、Q の核は P の値域となる。逆もまた然り。

このとき P を（核）V に沿った（値域）U の上への射影と言い、また Q を U に沿った V の上への射影と呼ぶ。

ベクトル空間の、部分空間の直和への分解は一般には一意的でない。従って、部分空間 V が与えられたとき、その値域（もしくは核）が V となるような射影は一般に複数存在しうる。

射影のスペクトルが {0, 1} に含まれることは

${\displaystyle (\lambda I-P)^{-1}={\frac {1}{\lambda }}I+{\frac {1}{\lambda (\lambda -1)}}P}$

から分かる。射影の固有値となれるのは 0 および 1 に限られるが、それらに対応する固有空間は射影の核および値域に他ならない。

自明でない射影は最小多項式が ${\displaystyle X^{2}-X=X(X-I)}$ となり、これは相異なる一次因子の積となっているから、P は対角化可能である。

考えているベクトル空間に内積が定義されていれば、直交性や（線型作用素の自己共軛性）といったような内積に付随するさまざまな概念を用いることができるようになる。直交射影は、値域 U と核 V とが互いに直交する部分空間になっているような射影をいう。射影が直交射影であるための必要十分条件は、それが自己共軛であること、即ち実ベクトル空間の場合には、ある直交基底に関する表現行列 P が対称行列（P = P^T）であり、複素ベクトル空間の場合には、表現行列 P がエルミート行列（P = (P^*)^T)）となることである。実際に、x, y が射影の定義域に属するベクトルのとき、 Px ∈ U, y − Py ∈ V であり、かつ ${\displaystyle \langle \bullet ,\bullet \rangle }$ を正定値内積として

${\displaystyle \langle Px,y-Py\rangle =(Px)^{\top }(y-Py)=x^{\top }(P^{\top }-P^{\top }P)y=x^{\top }(P-P^{\top }P)^{\top }y}$

が成り立つから、Px と y − Py とが任意の x, y に関して互いに直交するのは、P = P^TP（これは P = P^T かつ P = P² に同値）のときであり、かつそのときに限る^[3]。

直線の上への直交射影の場合が最も簡単であろう。直線上の単位ベクトル u をとれば、当該の射影は

${\displaystyle P_{u}=uu^{\top }}$

で与えられる。この作用素は u を変えないし、また u に直交する全てのベクトルを零化する。このことは、u を含むどんな直線の上への射影についても正しい^[4]。これを見るのに簡単な方法は、勝手なベクトル x を直線上の成分（つまり射影されたベクトルを考える）とそれに垂直な成分との和

${\displaystyle x:=x_{\parallel }+x_{\perp }}$

と考えることである。これに射影を施せば、平行なベクトル同士の内積と垂直なベクトル同士の内積の性質から

${\displaystyle P_{u}x=uu^{\top }x_{\parallel }+uu^{\top }x_{\perp }=u|x_{\parallel }|+u0=x_{\parallel }}$

を得る。

この等式は任意次元の部分空間の上への直交射影にも拡張することができる。u₁, ..., u_k を部分空間 U の正規直交基底とし、各列ベクトルが u₁, ..., u_k になっている k-次正方行列を A と書けば、所期の射影が

${\displaystyle P_{A}=AA^{\top }}$

で表される^[5]。これは内積を使えば

${\displaystyle P_{A}=\sum _{i}\langle u_{i},\bullet \rangle u_{i}}$

と書くこともできる。行列 A^T は U の直交成分が消える部分等距変換であり、A は U を考えている全体空間へ埋め込む等長変換になっている。従って P_A の値域は A の終空間 (final space) であり、また A^TA が U 上の恒等変換であることは明らかである。

上記の議論で正規直交条件は落とすこともできる。即ち、u₁, …, u_k を（必ずしも正規直交でない）基底とし、それらを列ベクトルに持つ行列を A と書けば、求める射影は

${\displaystyle P_{A}=A(A^{\top }A)^{-1}A^{\top }}$

と書ける^[6]。この場合も行列 A は U の全体空間への埋め込みになっているが、しかし一般にはもはや等距変換ではない。ここで行列 (A^TA)⁻¹ はノルムを回復する「正規化因子」である。実際、階数 1 の作用素 uu^T は ‖u‖ ≠ 1 のとき射影にならないが、これをu^Tu = ‖u‖² で割って得られる u(u^Tu)⁻¹u^T は u で張られる部分空間の上への射影になる。

この射影の値域となるベクトル空間が（基底ではなくて）枠 (frame) で張られているとき（つまり生成元の数が次元の値よりも大きいとき）には、上記の公式は

${\displaystyle P_{A}=A(A^{\top }A)^{+}A^{\top }}$

という形になる。ここで ${\displaystyle A^{+}}$ はムーア・ペンローズ擬似逆行列を表す。このような場合には、射影作用素を構成する方法は無数にあり、これはその無数の可能性のうちの一つに過ぎないことに注意すべきである。

あるいは、行列 ${\displaystyle [A\ B]}$ が正則で A^TB = 0（つまり、B は A の零空間行列）のときには

${\displaystyle I=A(A^{\top }A)^{-1}A^{\top }+B(B^{\top }B)^{-1}B^{\top }}$

が成り立つ。直交条件を強めて、正則行列 W に対して A^TWB = A^TW^TB = 0 が成り立つものとすれば、

${\displaystyle I={\begin{bmatrix}A&B\end{bmatrix}}{\begin{bmatrix}(A^{\top }WA)^{-1}A^{\top }\\(B^{\top }WB)^{-1}B^{\top }\end{bmatrix}}W}$

が成立する。

これらの公式は（転置行列を随伴行列に取り替えれば）複素内積空間でも成立する。

直交射影でないような射影のことを、斜交射影と呼ぶこともある。直交射影ほど頻繁ではないが、この種の射影は二次元に描画された空間図形を表すのにも用いられる。

斜交射影はその値域と核によって定まり、与えられた値域と核を持つ射影の行列表現の式は次のように求められる。まず射影の値域の基底を成すベクトルを u₁, …, u_k とし、それらを列ベクトルとして並べた n × k 行列を A と書く。射影の値域と核とは互いに補空間になっているから、核の次元は n − k である。従って、射影の核の直交補空間の次元は k であり、v₁, …, v_k がその基底を成すものとして、それらを並べた行列を B と書く。このとき、当該の射影は

${\displaystyle P=A(B^{\top }A)^{-1}B^{\top }}$

によって定まる。この公式を、上で直交射影に対してやったように拡張することもできる^[7]。

体上の d-次元ベクトル空間上の射影 P = P² は、その最小多項式が x² − x で相異なる一次因子の積に分解されるから、対角化可能である。従って、適当な基底を選べば P は、r を P の階数として

${\displaystyle P=I_{r}\oplus 0_{d-r}}$

なる形に表すことができる。ここで、I_r は r-次単位行列、0_d−r は次数 d − r の零行列である。複素ベクトル空間で内積を持つ場合には、適当な正規直交基底を選んで、P の表現行列を

${\displaystyle P={\begin{bmatrix}1&\sigma _{1}\\0&0\end{bmatrix}}\oplus \cdots \oplus {\begin{bmatrix}1&\sigma _{k}\\0&0\end{bmatrix}}\oplus I_{m}\oplus 0_{s}}$

なる形にすることができる^[8]。ただし、σ₁ ≥ σ₂ ≥ … ≥ σ_k > 0 とする。また、k, s, m は整数で、実数 σ_i は一意に定まる。2k + s + m = d であることに注意せよ。このときの、I_m ⊕ 0_s なる因子は、その上に P が直交射影として作用する最大の不変空間に対応しており（故に P 自体が直交射影となるのは k = 0 のとき、かつそのときに限る）、かつ σ_i-ブロックが P の斜交成分に対応している。

考えるベクトル空間 X が（有限次元とは限らない）ノルム空間のとき、（有限次元の場合には関係ないが）解析学的なことも考えないといけないので、ここでは X はバナッハ空間であることを仮定する。

先に述べた代数的な概念の多くはこの文脈においても有効である。例えば、互いに補空間となるような部分空間への X の直和分解が与えられればやはり射影が定まるし、逆に射影からそのような直和分解が得られる。実際、X が直和分解 X = U ⊕ V を持つとき、P(u + v) = u で定義される作用素はやはり値域 U および核 V の射影である（P² = P は明らかである）。一方 P が X 上の射影、即ち P² = P を満たすならば (I − P)² = (I − P) は容易に確かめられ、即ち (I − P) もまた射影となる。関係式 I = P + (I − P) から X が Ran(P) ⊕ Ran(I − P) なる直和に分解されることが従う。

しかし、有限次元の場合とは対照的に、射影は一般に連続とは限らない。実際、X の部分空間 U がノルムの定める位相に関して閉でないときは U の上への射影は連続でない。同じことだが、連続な射影 P の値域は必ず閉部分空間でなければならない。更には、連続射影の（実は一般の連続線型作用素の）核は閉部分空間である。従って、連続射影 P は X の互いに補空間となる閉部分空間の直和への分解 X = Ran(P) ⊕ Ker(P) = Ran(P) ⊕ Ran(I − P) を与える。

逆は、適当な仮定を追加すれば成り立つ。U を X の閉部分空間とすると、X = U ⊕ V となる閉部分空間 V が存在する場合に限り、値域が U, 核が V となる射影 P は連続である。これは閉グラフ定理から従う。即ち、x_n → x かつ Px_n → y とするとき、Px = y が示されればよい。U が閉で、{Px_n} ⊂ U だから y は U に属し、Py = y が成り立つ。また、x_n − Px_n = (I − P)x_n → x − y である。このとき、V は閉で {(I − P)x_n} ⊂ V だったから、x − y ∈ V 即ち P(x − y) = Px − Py = Px − y = 0 を得て、主張が示される。

今の議論では U, V がともに閉であるという仮定が効いているが、閉部分空間 U が与えられたときにその閉補空間 V の存在は一般には保証されない。ただし、ヒルベルト空間では直交補空間をとることで常にそれができる。バナッハ空間の場合には、一次元部分空間が常に閉補空間を持つことが、ハーン・バナッハの定理から直ちに従う。実際、U を u が張る一次元部分空間とすると、ハーン・バナッハから、有界線型汎函数 φ で φ(u) = 1 なるものがとれる。このとき、作用素 P(x) := φ(x)u は P² = P を満足し、射影となる。φ の有界性から P の連続性が出るから、従って Ker(P) = Ran(I − P) が U の閉補空間となる。

そうは言うものの、開写像定理により、バナッハ空間上の任意の連続射影は開写像であることが言える。

射影（直交射影とその他）は、線形代数の問題でのいくつかの計算アルゴリズムにおいて、重要な役割を果たす。

• QR分解 (ハウスホルダー変換とグラム・シュミットの正規直交化法を参照)
• 特異値分解
• ヘッセンベルク形式 への変換 (多くの固有値計算アルゴリズムでの最初の処理)
• 線形回帰

上で述べたように、射影というのは冪等作用素の特別なものであり、解析学的には直交射影は特性函数の非可換な一般化になっている。可測集合の特性函数を考えることから測度論が始まったように、冪等作用素は（例えば半単純多元環などの）分類にも用いられ、それゆえ想像のつくとおり、射影作用素も作用素環論の文脈で極めて頻繁に用いられる。特に、フォン・ノイマン環はその射影の成す完備束によって生成される。

量子論では，ある条件を満たす状態の全体は状態空間（英語版）の部分空間と考えることができるので，量子力学的な命題と部分空間，すなわち射影演算子とを対応させることができる(量子論理)．

統計力学では、運動の粗視化を射影演算子を使って定式化する方法(射影演算子の方法)がある．

分子対称性、分子振動、格子振動、結晶の波動関数では、任意の関数からある対称性に従う関数のみを作りたい時に、射影演算子が用いられる。たとえば射影演算子を用いれば、既約表現の表現行列からその基底関数（基準振動、基準モードなど）を求めることができる。

より一般に、ノルム空間の間の写像 T: V → W が与えられたとき、同じようにこれが核の直交補空間上の等距写像となることを要求することができる。その ${\displaystyle (\ker T)^{\perp }\to W}$ は等距であり、特に全射でなければならない。直交射影の場合というのは W が V の部分空間であるときである。リーマン幾何学においてこのことはリーマン沈め込みの定義に使われている。

• Dunford, N.; Schwartz, J. T. (1958). Linear Operators, Part I: General Theory. Interscience. Zbl 0084.10402 
• Meyer, Carl D. (2000). Matrix Analysis and Applied Linear Algebra. Society for Industrial and Applied Mathematics. ISBN 978-0-89871-454-8. Zbl 0962.15001. http://www.matrixanalysis.com/ 
• Reed, Michael; Simon, Barry (1980). Methods of modern mathematical physics I: Functional analysis (Rev. and enl. ed.). Academic Press. ISBN 0-12-585050-6. MR0751959. Zbl 0459.46001. https://books.google.co.jp/books?id=fXX0j4qa8G8C 
• 齋藤, 正彦『線型代数入門』（初版）東京大学出版会〈基礎数学1〉、1966年。ISBN 978-4-13-062001-7。http://www.utp.or.jp/bd/4-13-062001-0.html。 
• 黒田, 成俊『関数解析』共立出版株式会社〈共立数学講座 15〉、1980年。ISBN 978-4-320-01106-9。 

• Centering matrix, which is an example of a projection matrix.
• 直交化
• 不変部分空間
• 跡
• ダイクストラの射影アルゴリズム (Dykstra's projection algorithm): to compute the projection onto an intersection of sets

• MIT Linear Algebra Lecture on Projection Matrices at Google Video, from MIT OpenCourseWare
• Planar Geometric Projections Tutorial - a simple-to-follow tutorial explaining the different types of planar geometric projections.

表 話 編 歴 線型代数学・行列解析
連立一次方程式	ガウスの消去法 クラメルの公式 ガウス＝ザイデル法 ヤコビ法
ベクトル	線型独立 線型結合 基底 双対基底
ベクトル空間	双対空間 核空間 固有空間 広義固有空間 線型包 行空間 列空間 次元
計量ベクトル空間	ドット積 コーシー＝シュワルツの不等式 直交 正規直交系 正規直交基底 グラム・シュミットの正規直交化法 直交補空間
行列・線型写像	演算・操作 乗法 転置 逆行列 サラスの方法 基本変形 対角化 分解 LU QR コレスキー シューア 特異値 固有値 不変量 行列式 跡 階数 固有値と固有ベクトル 固有多項式 最小多項式 単因子 階数標準形 スミス標準形 ジョルダン標準形 有理標準形 小行列式 クラス 正則 基本 対称 エルミート 正規 直交 回転 ユニタリ 冪零 射影 正定値 ユニモジュラー 置換 区分
行列式	余因子展開 余因子行列 ヴァンデルモンドの行列式 終結式 コーシー・ビネの公式
多重線型代数	外積 外積代数 対称代数 テンソル代数
数値線形代数	基本的な概念 浮動小数点 数値的安定性 疎行列 Z-行列 M行列 条件数 ゲルシュゴリンの定理 クリロフ部分空間 ソフトウェア MATLAB 数値解析ソフトの比較/一覧 ライブラリ Armadillo Basic Linear Algebra Subprograms (BLAS) INTLAB Intel oneAPI Math Kernel Library LAPACK NumPy OpenBLAS 線型代数学ライブラリの比較 反復法・技法 SOR法 共役勾配法 GMRES法 固有値問題の数値解法 ランチョス法 QR法 べき乗法 逆べき乗法 ヤコビ法 (固有値問題) シュトラッセンのアルゴリズム ハウスホルダー変換 ギブンス回転 人物 ジェームズ・H・ウィルキンソン クリーブ・モラー ニコラス・ハイアム ジーン・ゴラブ リチャード・バルガ
行列値関数	行列指数関数 行列の対数 行列の平方根
その他	スカラー ケイリー・ハミルトンの定理 ペロン＝フロベニウスの定理 シューア補行列 シルヴェスターの慣性法則
カテゴリ