Багатократний інтеграл

Ця стаття містить правописні, лексичні, граматичні, стилістичні або інші мовні помилки, які треба виправити. Ви можете допомогти вдосконалити цю статтю, погодивши її із чинними мовними стандартами.

Багатокра́тний інтегра́л це обмежений інтеграл функції, що має декілька дійсних змінних, наприклад, f(x, y) або f(x, y, z). Інтеграли функцій двох змінних в області R² називають подвійними інтегралами, а інтеграли функції трьох змінних в області визначення R³ — потрійними інтегралами:^[1]

• подвійний інтеграл:

  ${\displaystyle \int \int f(x,y)\;dx\;dy}$

• потрійний інтеграл:

  ${\displaystyle \int \int \int f(x,y,z)\;dx\;dy\;dz}$

Так само як і звичайний інтеграл додатної функції однієї змінної задає площу області між графіком функції і віссю x, подвійний інтеграл додатної функції двох змінних визначає об'єм області між поверхнею, що визначається функцією (у тривимірній системі декартових координат де z = f(x, y)) і площиною, що задає її область визначення. ^[1] Якщо функція має більше змінних, багатократний інтеграл буде задавати гіпероб'єм багатовимірної функції.

Багатократний інтеграл функції із n змінними: f(x₁, x₂, ..., x_n) по області D зазвичай позначають за допомогою послідовних знаків інтегралу в зворотньому порядку виконання (інтеграл позначений знаком зліва буде розраховуватися останнім), за якими записується функція і аргументи інтегрування у відповідному порядку (крайній правий інтеграл буде розраховуватися в першу чергу). Область інтегрування позначається або символічно для кожного аргументу над кожним знаком інтегралу або, або в скороченій формі задається змінною біля інтегралу , що знаходиться праворуч від усіх:^[2]

${\displaystyle \int \cdots \int _{\mathbf {D} }\,f(x_{1},x_{2},\ldots ,x_{n})\,dx_{1}\!\cdots dx_{n}}$

Нехай функція ${\displaystyle f\left(x,y\right)}$ приймає в області ${\displaystyle \ D}$ тільки додатні значення. Тоді подвійний інтеграл ${\displaystyle \iint \limits _{D}{f\left(x,y\right)d\sigma }}$ чисельно дорівнює об'єму ${\displaystyle \ V}$ вертикального циліндрового тіла, побудованого на остові ${\displaystyle \ D}$ і обмеженого зверху відповідним шматком поверхні ${\displaystyle z=f\left(x,y\right)}$.

Для n > 1, розглянемо так звану "пів-відкриту" n-вимірну гіперпрямокутну область значень T, визначену наступним чином:

${\displaystyle T=[a_{1},b_{1})\times [a_{2},b_{2})\times \cdots \times [a_{n},b_{n})\subseteq \mathbf {R} ^{n}.}$

Розіб'ємо кожен інтервал [a_j, b_j) на скінченну послідовність підінтервалів I_j, що не перекриваються i_jα, де кожен підінтервал є закритим з лівого краю, і відкритим з правого краю.

Скінченна кількість підпрямокутників C буде визначатися наступним чином

${\displaystyle C=I_{1}\times I_{2}\times \cdots \times I_{n}}$

і є розбиттям області T; таке що, підпрямокутники C_k не перекриваються, а їх об'єднання буде утворювати T.

Нехай f : T → R є функцією визначеною в області T. Розглянемо розбиття C області T описане вище, так що C є сімейством із m підпрямокутниками C_m і

${\displaystyle T=C_{1}\cup C_{2}\cup \cdots \cup C_{m}}$

Ми можемо апроксимувати загальний (n + 1)-вимірний об'єм, що обмежує собою n-вимірний гіперпрямокутник T і зверху обмежений n-вимірним графіком функції f за допомогою наступної суми Рімана:

${\displaystyle \sum _{k=1}^{m}f(P_{k})\,\operatorname {m} (C_{k})}$

де P_k це точка в C_k і m(C_k) є добуток довжин інтервалів, декартовий добуток яких дорівнює C_k.

Діаметр підпрямокутника C_k буде дорівнювати найбільшій довжині інтервала декартовим добутком якого є C_k. Діаметр даного розбиття T визначається найбільшим діаметром підпрямокутника в розбитті. Інтуїтивно, із обмеженням діаметру розбиття C до все менших і менших значень, кількість підпрямокутників m стає більшою, а міра m(C_k) для кожного підпрямокутника стає меншою. Функцію f називають такою, що має Ріманів інтеграл якщо існує границя

${\displaystyle S=\lim _{\delta \to 0}\sum _{k=1}^{m}f(P_{k})\,\operatorname {m} \,(C_{k})}$

де границя знаходиться для всіх можливих варіантів розбиття T із діаметром δ.^[3]

Якщо f інтегрована за Ріманом, то S називають Рімановим інтегралом функції f по області T і позначається наступним чином

${\displaystyle \int \cdots \int _{T}\,f(x_{1},x_{2},\ldots ,x_{n})\,dx_{1}\!\cdots dx_{n}}$

Часто цей запис скорочують до наступного вигляду

${\displaystyle \int _{T}\!f(\mathbf {x} )\,d^{n}\mathbf {x} .}$

де x позначає n-кортеж (x₁, ... x_n) і dⁿx позначає n-вимірний об'ємний диференціал.

Багатократні інтеграли мають більшість властивостей, що є спільними із звичайними інтегралами функцій однієї змінної (лінійність, комутативність, монотонність тощо). Однією з важливих властивостей багатократного інтегралу є те, що значення інтегралу не залежить від порядку інтегрування при певних умовах. Ця властивість відома як Теорема Фубіні.^[4]

Вирішення задачі багатократного інтегрування, в більшості випадків, полягає у знаходженні способу спростити багатократний інтеграл у послідовний інтеграл із інтегралів однієї змінної, кожен з яких має прямий розв'язок. Для неперервних функцій, це підтверджується Теоремою Фубіні. Іноді, можливо отримати результат за допомогою прямого дослідження без розрахунків.

Далі наведені найпростіші методи інтегрування:^[1]

Якщо під інтегралом знаходиться константна функція c, інтеграл буде дорівнювати добутку c на вимір області інтегрування. Якщо c = 1, а область є частиною області R², тоді інтеграл визначає площу області, якщо область буде частиною R³, тоді інтеграл повертає об'єм.

Наприклад. Нехай f(x, y) = 2 і

${\displaystyle D=\left\{(x,y)\in \mathbf {R} ^{2}\ :\ 2\leq x\leq 4\ ;\ 3\leq y\leq 6\right\}}$

в такому випадку

${\displaystyle \int _{3}^{6}\int _{2}^{4}\ 2\ dx\,dy=2\int _{3}^{6}\int _{2}^{4}\ 1\ dx\,dy=2\cdot {\mbox{area}}(D)=2\cdot (2\cdot 3)=12}$,

оскільки із визначення ми маємо наступне:

${\displaystyle \int _{3}^{6}\int _{2}^{4}\ 1\ dx\,dy={\mbox{area}}(D).}$

Якщо область інтегрування симетрична відносно початку координат по відношенню хоча б до однієї із змінних інтегрування, а функція що інтегрується є парною по відношенню до цієї змінної, інтеграл дорівнюватиме нулю, оскільки інтеграли над двома половинами області будуть мати однаковий абсолютний об'єм але протилежні знаки. Якщо функція, яка інтегрується є непарною по відношенню до такої змінної, інтеграл дорівнює двом інтегралам для половини цієї області, оскільки значення інтегралів двох половин є рівними.

Приклад 1. Розглянемо функцію f(x,y) = 2 sin(x) − 3y³ + 5 що інтегрується по області

${\displaystyle T=\left\{(x,y)\in \mathbf {R} ^{2}\ :\ x^{2}+y^{2}\leq 1\right\},}$

диск із радіусом 1 має центр в початку координат, із включеною межею.

Застосовуючи властивість лінійності, вважаємо, що інтеграл можна розділити на три частини:

${\displaystyle \iint _{T}\left(2\sin x-3y^{3}+5\right)\,dx\,dy=\iint _{T}2\sin x\,dx\,dy-\iint _{T}3y^{3}\,dx\,dy+\iint _{T}5\,dx\,dy}$

Функція 2 sin(x) є парною функцією для змінної x а диск T є симетричним відносно осі y, тому значення першого інтегралу дорівнює 0. Аналогічно, функція 3y³ є парною функцією для y, а T симетрична відносно осі x, і таким чином є єдиною складовою, що впливає на остаточний результат є третій інтеграл. Таким чином початковий інтеграл дорівнює площі диска помноженій на 5, або 5π.

Приклад 2. розглянемо функцію f(x, y, z) = x exp(y² + z²), оскільки область інтегрування є сферою із радіусом 2 із центром у початку координат,

${\displaystyle T=\left\{(x,y,z)\in \mathbf {R} ^{3}\ :\ x^{2}+y^{2}+z^{2}\leq 4\right\}.}$

"Шар" є симетричним відносно всіх трьох осей, але достатньо привести інтеграл по осі x аби показати що він дорівнює нулю 0, оскільки функція є парною функцією відносно цієї змінної.

Границі інтегрування часто не є просто взаємозамінними (без нормалізації або через складну формулу інтегрування). Виконують заміну змінних аби переписати інтеграл таким чином, аби інтегрувати у більш "зручній" області, яку можна описати простішою формулою. Аби це зробити, функцію необхідно привести до нових координат.

Приклад 1a. Функція дорівнює f(x, y) = (x − 1)² + √y; якщо застосувати заміну x′ = x − 1, y′ = y так що x = x′ + 1, y = y′ буде одержана нова функція f₂(x, y) = (x′)² + √y.

• Аналогічно для області інтегрування, оскільки вона обмежує початкові змінні (x і y, які були перетворені вище в прикладі).
• диференціали dx і dy трансформуються за допомогою абсолютного значення детермінанта матриці Якобі, що містить частинні похідні перетворення відповідно до нової змінної (розглянемо, як приклад, диференційне перетворення в полярних координатах).

Існує три основні "види" заміни змінних (один для R², два для R³); однак, в більш загальному випадку заміни можна виконувати за аналогічним принципом.

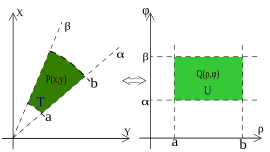
Для R² якщо область має кругову симетрію а функція має деякі відповідні характеристики може бути корисним застосувати трансформування в полярні координати (дивись приклад на зображенні). Це означає що загальні точки P(x, y) в декартовій системі координат зміняться відповідними точками в полярній системі координат. Що дозволяє змінити форму області і спростити операції.

Основне рівняння за допомогою якого здійснюється перетворення буде наступним:

${\displaystyle f(x,y)\rightarrow f(\rho \cos \varphi ,\rho \sin \varphi ).}$

Приклад 2a. Функцією є f(x, y) = x + y, застосувавши перетворення отримаємо

${\displaystyle f(\rho ,\varphi )=\rho \cos \varphi +\rho \sin \varphi =\rho (\cos \varphi +\sin \varphi ).}$

Приклад 2b. Функцією є f(x, y) = x² + y², в такому випадку маємо:

${\displaystyle f(\rho ,\varphi )=\rho ^{2}\left(\cos ^{2}\varphi +\sin ^{2}\varphi \right)=\rho ^{2}}$

використовуючи тригонометричну тотожність Піфагора.

Перетворення області виконано за допомогою визначення величини радіусу і величини описаного кута за допомогою інтервалів ρ, φ від початкових x, y.

Приклад 2c. Область задається як D = {x² + y² ≤ 4}, це коло радіусом 2; очевидно, що кут який воно покриває це кут усього кола, тому φ змінюється від 0 до 2π, в той час як радіус змінюється від 0 до 2.

Приклад 2d. Область задається як D = {x² + y² ≤ 9, x² + y² ≥ 4, y ≥ 0}, це кругла дуга в додатній відносно осі y півплощині (див. малюнок); φ описує площину із зміною кута ρ в діапазоні значень від 2 до 3. Таким чином перетворена область буде таким прямокутником:

${\displaystyle T=\{2\leq \rho \leq 3,\ 0\leq \varphi \leq \pi \}.}$

Детермінант матриці Якобі для такого перетворення буде таким:

${\displaystyle {\frac {\partial (x,y)}{\partial (\rho ,\varphi )}}={\begin{vmatrix}\cos \varphi &-\rho \sin \varphi \\\sin \varphi &\rho \cos \varphi \end{vmatrix}}=\rho }$

який було отримано відповідно до часткових похідних для x = ρ cos(φ), y = ρ sin(φ) в першому стовбці відповідно до ρ і в другому стовпці відповідно до φ, так що диференціали dx dy в цьому перетворенні стали замінені на ρ dρ dφ.

Так як функція була перетворена а області були розраховані, стає можливим визначити формулу для заміни змінних в полярних координатах:

${\displaystyle \iint _{D}f(x,y)\,dx\,dy=\iint _{T}f(\rho \cos \varphi ,\rho \sin \varphi )\rho \,d\rho \,d\varphi .}$

φ є дійсним для інтервалу [0, 2π] в той час як ρ, що є мірою довжини, може приймати лише додатні значення.

Приклад 2e. Функцією є f(x, y) = x а область є такою ж як в прикладі 2d. Із попередніх розрахунків для D ми вже знаємо інтервали для ρ (з 2 до 3) і для φ (з 0 до π). Тепер ми змінюємо функцію:

${\displaystyle f(x,y)=x\longrightarrow f(\rho ,\varphi )=\rho \cos \varphi .}$

нарешті, застосуємо формулу інтегрування:

${\displaystyle \iint _{D}x\,dx\,dy=\iint _{T}\rho \cos \varphi \rho \,d\rho \,d\varphi .}$

Оскільки інтервали відомі, матимемо

${\displaystyle \int _{0}^{\pi }\int _{2}^{3}\rho ^{2}\cos \varphi \,d\rho \,d\varphi =\int _{0}^{\pi }\cos \varphi \ d\varphi \left[{\frac {\rho ^{3}}{3}}\right]_{2}^{3}={\Big [}\sin \varphi {\Big ]}_{0}^{\pi }\ \left(9-{\frac {8}{3}}\right)=0.}$

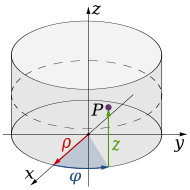
В R³ інтегрування областей що мають круглу основу можна здійснювати за допомогою переходу до циліндричних координат; перетворення функції виконується за допомогою наступних рівнянь:

${\displaystyle f(x,y,z)\rightarrow f(\rho \cos \varphi ,\rho \sin \varphi ,z)}$

Область трансформації можна отримати графічним чином, оскільки змінюється лише форма основи, в той час як висота залежить від форми початкового регіону.

Приклад 3a. Регіоном є D = {x² + y² ≤ 9, x² + y² ≥ 4, 0 ≤ z ≤ 5} (тобто "труба" основа якої є круглим сектором з прикладу 2d і висота якого дорівнює 5); після застосування перетворення, буде отримана область:

${\displaystyle T=\{2\leq \rho \leq 3,\ 0\leq \varphi \leq 2\pi ,\ 0\leq z\leq 5\}}$

(це буде паралелепіпед, основа якого подібна до прямокутника з прикладу 2d і висота якого дорівнює 5).

Оскільки компонент z не змінюється під час перетворення, диференціали dx dy dz змінюються при переході до полярних координат: таким чином вони перетворюються на ρ dρ dφ dz.

Врешті-решт, стає можливим застосувати остаточну формулу до циліндричних координат:

${\displaystyle \iiint _{D}f(x,y,z)\,dx\,dy\,dz=\iiint _{T}f(\rho \cos \varphi ,\rho \sin \varphi ,z)\rho \,d\rho \,d\varphi \,dz.}$

Цей метод зручно застосовувати у випадку, коли області є циліндричними або конічними або для областей, де легко виділити інтервал z і перетворити круглу основу і функцію.

Приклад 3b. Функція задана як f(x, y, z) = x² + y² + z а область інтегрування є циліндром: D = {x² + y² ≤ 9, −5 ≤ z ≤ 5 }. Перетворення D в циліндричні координати є наступним:

${\displaystyle T=\{0\leq \rho \leq 3,\ 0\leq \varphi \leq 2\pi ,\ -5\leq z\leq 5\}.}$

а функція перетворюється на

${\displaystyle f(\rho \cos \varphi ,\rho \sin \varphi ,z)=\rho ^{2}+z}$

Тепер можна застосувати формулу для інтегрування:

${\displaystyle \iiint _{D}\left(x^{2}+y^{2}+z\right)\,dx\,dy\,dz=\iiint _{T}\left(\rho ^{2}+z\right)\rho \,d\rho \,d\varphi \,dz;}$

продовжуючи перетворення формули отримаємо

${\displaystyle \int _{-5}^{5}dz\int _{0}^{2\pi }d\varphi \int _{0}^{3}\left(\rho ^{3}+\rho z\right)\,d\rho =2\pi \int _{-5}^{5}\left[{\frac {\rho ^{4}}{4}}+{\frac {\rho ^{2}z}{2}}\right]_{0}^{3}\,dz=2\pi \int _{-5}^{5}\left({\frac {81}{4}}+{\frac {9}{2}}z\right)\,dz=\cdots =405\pi .}$

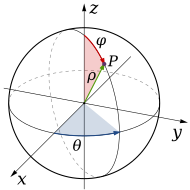
В R³ деякі області мають сферичну симетрію, таким чином можливо задати координати кожної точки області інтегрування за допомогою двох кутів і однієї відстані. Для цього можливо скористатися переходом до сферичної системи координат; функція перетворюється за допомогою наступних рівнянь:

${\displaystyle f(x,y,z)\longrightarrow f(\rho \cos \theta \sin \varphi ,\rho \sin \theta \sin \varphi ,\rho \cos \varphi )}$

Точки на осі z не можна точно характеризувати в сферичних координатах, тому θ може змінюватися між значеннями 0 і 2π.

Найкращою областю інтегрування для цього переходу очевидно є сфера.

Приклад 4a. Область задана як D = x² + y² + z² ≤ 16 (сфера із радіусом 4 і центром в початку координат); застосувавши перетворення отримаємо область

${\displaystyle T=\{0\leq \rho \leq 4,\ 0\leq \varphi \leq \pi ,\ 0\leq \theta \leq 2\pi \}.}$

Детермінант якобіану для цього перетворення буде наступним:

${\displaystyle {\frac {\partial (x,y,z)}{\partial (\rho ,\theta ,\varphi )}}={\begin{vmatrix}\cos \theta \sin \varphi &-\rho \sin \theta \sin \varphi &\rho \cos \theta \cos \varphi \\\sin \theta \sin \varphi &\rho \cos \theta \sin \varphi &\rho \sin \theta \cos \varphi \\\cos \varphi &0&-\rho \sin \varphi \end{vmatrix}}=\rho ^{2}\sin \varphi }$

Диференціали dx dy dz таким чином перетворюються на ρ² sin(φ) dρ dθ dφ.

Це приводить до остаточної формули інтегрування:

${\displaystyle \iiint _{D}f(x,y,z)\,dx\,dy\,dz=\iiint _{T}f(\rho \sin \varphi \cos \theta ,\rho \sin \varphi \sin \theta ,\rho \cos \varphi )\rho ^{2}\sin \varphi \,d\rho \,d\theta \,d\varphi .}$

Цей метод краще використовувати у випадках, коли область сферична і коли функцію можна легко спростити за допомогою першої тригонометричної тотожності узагальненої для R³ (див. приклад 4b); в інших випадках більш вдалим може бути застосування циліндричних координат (див. приклад 4c).

${\displaystyle \iiint _{T}f(a,b,c)\rho ^{2}\sin \varphi \,d\rho \,d\theta \,d\varphi .}$

Додаткові ρ² і sin φ взяті із Якобіана.

В наступних прикладах ролі φ і θ були замінені навпаки.

Приклад 4b. D є такою ж областю як і в прикладі 4a, а f(x, y, z) = x² + y² + z² є функцією що інтегрується. Її перетворення дуже просте:

${\displaystyle f(\rho \sin \varphi \cos \theta ,\rho \sin \varphi \sin \theta ,\rho \cos \varphi )=\rho ^{2},}$

ми знаємо інтервали перетвореної області T із D:

${\displaystyle T=\{0\leq \rho \leq 4,\ 0\leq \varphi \leq \pi ,\ 0\leq \theta \leq 2\pi \}.}$

Таким чином застосовуємо формулу інтегрування:

${\displaystyle \iiint _{D}\left(x^{2}+y^{2}+z^{2}\right)\,dx\,dy\,dz=\iiint _{T}\rho ^{2}\,\rho ^{2}\sin \theta \,d\rho \,d\theta \,d\varphi ,}$

і з цього ми отримаємо

${\displaystyle \iiint _{T}\rho ^{4}\sin \theta \,d\rho \,d\theta \,d\varphi =\int _{0}^{\pi }\sin \varphi \,d\varphi \int _{0}^{4}\rho ^{4}d\rho \int _{0}^{2\pi }d\theta =2\pi \int _{0}^{\pi }\sin \varphi \left[{\frac {\rho ^{5}}{5}}\right]_{0}^{4}\,d\varphi =2\pi \left[{\frac {\rho ^{5}}{5}}\right]_{0}^{4}{\Big [}-\cos \varphi {\Big ]}_{0}^{\pi }={\frac {4096\pi }{5}}.}$

Приклад 4c. Область D це шар із центром в початку координат і радіусом 3a,

${\displaystyle D=\left\{x^{2}+y^{2}+z^{2}\leq 9a^{2}\right\}}$

а f(x, y, z) = x² + y² - функція інтегрування.

Зважаючи на область інтегрування, зручним має бути використати перехід в сферичну систему координат, на справді, інтервали нових змінних які обмежують нову область T є очевидними:

${\displaystyle T=\{0\leq \rho \leq 3a,\ 0\leq \varphi \leq 2\pi ,\ 0\leq \theta \leq \pi \}.}$

Однак, застосувавши перетворення ми отримаємо

${\displaystyle f(x,y,z)=x^{2}+y^{2}\longrightarrow \rho ^{2}\sin ^{2}\theta \cos ^{2}\varphi +\rho ^{2}\sin ^{2}\theta \sin ^{2}\varphi =\rho ^{2}\sin ^{2}\theta }$.

Застосувавши формулу інтегрування, отримаємо:

${\displaystyle \iiint _{T}\rho ^{2}\sin ^{2}\theta \rho ^{2}\sin \theta \,d\rho \,d\theta \,d\varphi =\iiint _{T}\rho ^{4}\sin ^{3}\theta \,d\rho \,d\theta \,d\varphi }$

що є дуже складним для розв'язку. Цю проблему спробуємо вирішити переходом у циліндричну систему координат. Нові інтервали для T будуть наступними

${\displaystyle T=\left\{0\leq \rho \leq 3a,\ 0\leq \varphi \leq 2\pi ,\ -{\sqrt {9a^{2}-\rho ^{2}}}\leq z\leq {\sqrt {9a^{2}-\rho ^{2}}}\right\};}$

інтервал z було отримано за допомогою розділення кулі на дві напівсфери шляхом вирішення нерівності із формули для D (і виконавши пряме перетворення x² + y² у ρ²). Нова функція тоді буде простою ρ². Застосовуючи формулу інтегрування

${\displaystyle \iiint _{T}\rho ^{2}\rho \ d\rho d\varphi dz}$.

Тоді ми отримаємо

${\displaystyle {\begin{aligned}\int _{0}^{2\pi }d\varphi \int _{0}^{3a}\rho ^{3}d\rho \int _{-{\sqrt {9a^{2}-\rho ^{2}}}}^{\sqrt {9a^{2}-\rho ^{2}}}\,dz&=2\pi \int _{0}^{3a}2\rho ^{3}{\sqrt {9a^{2}-\rho ^{2}}}\,d\rho \\&=-2\pi \int _{9a^{2}}^{0}(9a^{2}-t){\sqrt {t}}\,dt&&t=9a^{2}-\rho ^{2}\\&=2\pi \int _{0}^{9a^{2}}\left(9a^{2}{\sqrt {t}}-t{\sqrt {t}}\right)\,dt\\&=2\pi \left(\int _{0}^{9a^{2}}9a^{2}{\sqrt {t}}\,dt-\int _{0}^{9a^{2}}t{\sqrt {t}}\,dt\right)\\&=2\pi \left[9a^{2}{\frac {2}{3}}t^{\frac {3}{2}}-{\frac {2}{5}}t^{\frac {5}{2}}\right]_{0}^{9a^{2}}\\&=2\cdot 27\pi a^{5}\left(6-{\frac {18}{5}}\right)\\&={\frac {648\pi }{5}}a^{5}.\end{aligned}}}$

Завдяки переходу в циліндричні координати стало можливим спростити потрійний інтеграл до простого інтегралу з однією змінною.

Припустимо, що ми хочемо проінтегрувати функцію багатьох змінних f по області A:

${\displaystyle A=\left\{(x,y)\in \mathbf {R} ^{2}\ :\ 11\leq x\leq 14\ ;\ 7\leq y\leq 10\right\}{\mbox{ and }}f(x,y)=x^{2}+4y\,}$

З цього ми записуємо формулювання багатократного інтегралу

${\displaystyle \int _{7}^{10}\int _{11}^{14}(x^{2}+4y)\,dx\,dy}$

Внутрішній інтеграл застосовується першим, інтегруючи відносно змінної x і приймаючи y за константу, так ніби вона не є змінною інтегрування. Результат цього інтегралу, що є функцією яка залежить від лише від змінної y, потім інтегрують по y.

${\displaystyle {\begin{aligned}\int _{11}^{14}\left(x^{2}+4y\right)\,dx&=\left[{\frac {1}{3}}x^{3}+4yx\right]_{x=11}^{x=14}\\&={\frac {1}{3}}(14)^{3}+4y(14)-{\frac {1}{3}}(11)^{3}-4y(11)\\&=471+12y\end{aligned}}}$

Тепер інтегруємо результат відносно y.

${\displaystyle {\begin{aligned}\int _{7}^{10}(471+12y)\ dy&={\Big [}471y+6y^{2}{\Big ]}_{y=7}^{y=10}\\&=471(10)+6(10)^{2}-471(7)-6(7)^{2}\\&=1719\end{aligned}}}$

Іноді, порядок інтегрування можна змінити місцями, тобто, інтегрування спочатку по x потім по y і навпаки дає однаковий результат. Наприклад, виконавши попередні розрахунки змінивши порядок навпаки приведе до того ж результату:

${\displaystyle {\begin{aligned}\int _{11}^{14}\int _{7}^{10}\,\left(x^{2}+4y\right)\,dy\,dx&=\int _{11}^{14}{\Big [}x^{2}y+2y^{2}{\Big ]}_{y=7}^{y=10}\,dx\\&=\int _{11}^{14}\,(3x^{2}+102)\,dx\\&={\Big [}x^{3}+102x{\Big ]}_{x=11}^{x=14}\\&=1719.\end{aligned}}}$

Умови при яких порядок можна змінювати визначає Теорема Фубіні.

Як правило, як і для випадку з однією змінною, багатократний інтеграл можна використовувати для пошуку середнього значення функції в рамках заданої множини. Дана множина D ⊆ Rⁿ і інтегрована функція f по D, середнє значення функції f по області задається наступним чином

${\displaystyle {\bar {f}}={\frac {1}{m(D)}}\int _{D}f(x)\,dx,}$

де m(D) це міра для D.

Крім того, багатократні інтеграли використовуються в багатьох задачах з фізики. Нижче наводяться приклади, які також показують деякі варіації в нотації.

В механіці, момент інерції розраховується як об'ємний інтеграл (потрійний інтеграл) густини зваженої як квадрат відстані від осі:

${\displaystyle I_{z}=\iiint _{V}\rho r^{2}\,dV.}$

Гравітаційний потенціал, що пов'язаний із розподіленням маси, що задається мірою Бореля для маси dm в тривимірному евклідовому просторі R³ буде задано як^[5]

${\displaystyle V(\mathbf {x} )=-\iiint _{\mathbf {R} ^{3}}{\frac {G}{|\mathbf {x} -\mathbf {y} |}}\,dm(\mathbf {y} ).}$

Якщо задана неперервна функція ρ(x), що задає густину розподілення для x, таким чином що dm(x) = ρ(x)d³x, де d³x є Евклідовим елементом об'єму, тоді гравітаційний потенціал дорівнює

${\displaystyle V(\mathbf {x} )=-\iiint _{\mathbf {R} ^{3}}{\frac {G}{|\mathbf {x} -\mathbf {y} |}}\,\rho (\mathbf {y} )\,d^{3}\mathbf {y} .}$

В електромагнетизмі, Рівняння Максвелла для розрахунку загального магнітного і електричного полів можна записати із використанням багатократного інтегралу.^[6] В наведеному прикладі, електричне поле, утворене через розподілення електричних зарядів задається за допомогою об'ємної густини заряду ρ(${\displaystyle {\vec {r}}}$) що розраховується за допомогою потрійного інтегралу векторної функції:

${\displaystyle {\vec {E}}={\frac {1}{4\pi \varepsilon _{0}}}\iiint {\frac {{\vec {r}}-{\vec {r}}'}{\left\|{\vec {r}}-{\vec {r}}'\right\|^{3}}}\rho ({\vec {r}}')\,d^{3}r'.}$

Це також можна записати як інтеграл, відповідно до мирі із врахуванням знаку, що буде задавати розподілення заряду.

• Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2024. — 2403 с.(укр.)
• Поняття про подвійний інтеграл // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 458. — 594 с.

Це незавершена стаття з математики. Ви можете допомогти проєкту, виправивши або дописавши її.