Riemannsche Zeta-Funktion
 Van Wikipedia, de gratis encyclopedie
Van Wikipedia, de gratis encyclopedie


Die Riemannsche Zeta-Funktion, auch Riemannsche ζ-Funktion oder Riemannsche Zetafunktion (nach Bernhard Riemann), ist eine komplexwertige, spezielle mathematische Funktion, die in der analytischen Zahlentheorie, einem Teilgebiet der Mathematik, eine wichtige Rolle spielt. Erstmals betrachtet wurde sie im 18. Jahrhundert von Leonhard Euler, der sie im Rahmen des Basler Problems untersuchte. Bezeichnet wird sie üblicherweise mit dem griechischen Buchstaben (Zeta).
Ihr Definitionsbereich umfasst alle komplexen Zahlen außer der Zahl . Für Werte mit Realteil größer als wird die Riemannsche Zeta-Funktion über eine Dirichlet-Reihe definiert. Sie lautet:
Mittels analytischer Fortsetzung kann sie zu einer auf holomorphen Funktion ausgeweitet werden. Sie erfüllt eine wichtige Funktionalgleichung, mit deren Hilfe sie sogar charakterisiert werden kann.
Von großer Bedeutung für die Zahlentheorie ist der Zusammenhang der Zeta-Funktion mit der Primfaktorzerlegung natürlicher Zahlen. Auf dieser Basis konnte Riemann im Jahr 1859 die sehr enge und nicht offensichtliche Beziehung zwischen den Primzahlen und der Lage der Nullstellen der Zeta-Funktion nachweisen. So folgt aus der Tatsache für alle komplexen Zahlen mit bereits, dass die -te Primzahl „recht genau“ den Wert hat – genauer gesagt folgt[1][2]
Hier bezeichnet den natürlichen Logarithmus von . Genauere Informationen über nullstellenfreie Bereiche macht das Bild um die Primzahlverteilung deutlicher. Die bisher unbewiesene Riemannsche Vermutung sagt aus, dass alle nicht-trivialen Nullstellen der Riemannschen Zeta-Funktion den Realteil haben, also auf einer gemeinsamen Geraden liegen. Ob diese Vermutung zutrifft, ist eines der wichtigsten ungelösten Probleme der Mathematik. Aufgrund der Bedeutung der Primzahlen für moderne Kryptosysteme (wie in etwa der RSA-Verschlüsselung) genießt die Riemannsche Vermutung auch außerhalb der reinen Zahlentheorie Aufmerksamkeit.
Das Verhalten der Riemannschen Zeta-Funktion in den Bereichen und gilt als gut verstanden. Jedoch sind ihre Eigenschaften innerhalb des kritischen Streifens weitestgehend unbekannt und Gegenstand bedeutender Vermutungen. Dies betrifft unter anderem die Fragen nach asymptotischem Wachstum in imaginärer Richtung und der für die Zahlentheorie so wichtigen Nullstellenverteilung. Nach heutigem Wissensstand beschreibt die Zeta-Funktion im Streifen im Wesentlichen Chaos. Die Werte der Nullstellen bauen nicht nur Brücken zur Theorie der Primzahlen, sondern höchstwahrscheinlich auch zur modernen Quantenphysik. Weitere Anwendungsgebiete sind die Wahrscheinlichkeitstheorie und die Theorie der automorphen Formen (insbesondere im Feld des Langlands-Programms).
Aus Sicht der algebraischen Zahlentheorie ist die Riemannsche Zeta-Funktion nur ein Spezialfall einer ganzen Klasse sogenannter L-Funktionen. So entspricht sie der zum Trivialen Charakter modulo 1 gehörigen Dirichletschen L-Funktion und der zum Zahlkörper (rationale Zahlen) korrespondierenden Dedekindschen Zeta-Funktion.
Wegen der überragenden Bedeutung der Riemannschen Vermutung für die Zahlentheorie und deren Anwendungen bleibt der Themenkreis der Riemannschen Zeta-Funktion ein Gebiet intensiver mathematischer Forschung. Entscheidende Fortschritte erzielten Mathematiker wie zum Beispiel Lindelöf, Hadamard, de La Vallée Poussin, Hardy, Littlewood, Selberg, Woronin und Conrey.
Notation[Bearbeiten | Quelltext bearbeiten]
Im ganzen Artikel bezeichnet die imaginäre Einheit und die Eulersche Zahl. Zudem wird häufig als komplexe Variable verwendet, die oft in zerlegt wird.
Des Weiteren wird oft die O-Notation von Landau für die Angabe von Fehlergrößen verwendet. Verhalten sich zwei (unbeschränkte) Funktionen und für wachsendes Argument gleich, gilt also , so wird dies mit notiert.
Einordnung ohne mathematisches Vorwissen[Bearbeiten | Quelltext bearbeiten]
Motivation[Bearbeiten | Quelltext bearbeiten]


Im Zentrum der Zahlentheorie, jenes Zweiges der Mathematik, der sich mit den Eigenschaften der natürlichen Zahlen 1, 2, 3, 4 … beschäftigt, stehen die Primzahlen 2, 3, 5, 7, 11 … Diese sind ausgezeichnet durch die Eigenschaft, genau zwei Teiler zu haben, nämlich die 1 und sich selbst. Die 1 ist keine Primzahl. Bereits Euklid konnte zeigen, dass es unendlich viele Primzahlen gibt, weshalb die Liste 2, 3, 5, 7, 11 … niemals enden wird.
Die Primzahlen sind gewissermaßen die Atome der ganzen Zahlen, da sich jede positive ganze Zahl eindeutig multiplikativ in solche zerlegen lässt. Zum Beispiel gilt 21 = 3 · 7 und 110 = 2 · 5 · 11. Trotz dieser elementaren Eigenschaft ist nach mehreren Jahrtausenden Mathematikgeschichte bis heute kein Muster bekannt, dem sich die Primzahlen in ihrer Folge unterwerfen. Ihre Natur ist eine der bedeutendsten offenen Fragen der Mathematik.
Auch wenn das detaillierte Verständnis der Sequenz 2, 3, 5, 7, 11 … unerreichbar fern ist, kann man nach Mustern suchen, wenn man den Blick ausweitet. Dabei hilft zum Beispiel die Vorstellung, dass mit Hilfe statistischer Methoden das Verhalten sehr vieler Menschen (zum Beispiel bezüglich des Konsum- und Wahlverhaltens) oft überraschend präzise beschrieben werden kann, obgleich ein einzelner Mensch äußerst komplex ist. Das hat grob gesagt damit zu tun, dass größer werdende relevante Datenmengen immer zuverlässigere Informationen liefern. Im Falle der Primzahlen führt eine solche Ausweitung unter anderem zu der Frage, wie viele Primzahlen es unterhalb einer fest gewählten Zahl gibt.
Zum Beispiel sind nur 4 Primzahlen, nämlich 2, 3, 5 und 7, kleiner als die Zahl 10. Im Falle von 50 gibt es schon 15 kleinere Primzahlen, nämlich
- 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47.
Ende des 19. Jahrhunderts konnte als Folgerung des Primzahlsatzes eine verblüffend genaue Abschätzung für die Verteilung der Primzahlen bewiesen werden. Der Primzahlsatz wurde bereits im 18. Jahrhundert vom 15-jährigen Gauß (in den Jahren 1792/93) vermutet.[3] Die Abschätzung wurde bereits vor einem Beweis des Primzahlsatzes von Riemann gegeben und tritt als eine Formel in Erscheinung, die die schnelle Berechnung eines Vorhersagewertes zulässt. Mit dieser Formel kann zu einer gegebenen Zahl die Anzahl der Primzahlen, die kleiner als diese Zahl sind, in vernünftiger Zeit geschätzt werden. Die Formel zur Vorhersage wird prozentual immer genauer, je größer die Zahl gewählt wird (jedoch mit Schwankungen). Beispielsweise liefert sie für den Wert 50 die Prognose 14,97 (es sind tatsächlich 15 Primzahlen, siehe oben), womit der Fehler bei 0,16 Prozent liegt. Weiter sagt sie rund 78.527 Primzahlen unter der Zahl 1.000.000 voraus – tatsächlich sind es 78.498. Dies entspricht einer Abweichung von 0,037 Prozent.
Ein mögliches Werkzeug zum Beweis dieser Formel ist die Riemannsche Zeta-Funktion. Dabei wird ausgenutzt, dass sie das Gesetz der eindeutigen Primfaktorzerlegung in der Sprache der Analysis ausdrückt. Also werden die Eigenschaften der Primzahlen in dieser Funktion versteckt abgespeichert. Erhöht sich das Wissen um die Zeta-Funktion, so auch das Wissen um die Primzahlen, sogar in detaillierteren Fragestellungen. So können viele Primzahltests, wie der von Miller-Rabin unter Annahme der Riemannschen Vermutung bewiesen bzw. verbessert werden.[4]
Die Nullstellen der Zeta-Funktion erzeugen einen Korrekturterm obiger Formel, der sie in einen exakten Ausdruck umwandelt. Diese dadurch entstehende exakte Formel kennt also die Verteilung der Primzahlen bis ins letzte Detail. Damit gelten die Fragen um die Primzahlen jedoch nicht als gelöst: der Rechenaufwand nimmt mit steigenden Werten sehr stark zu und somit sind praktische Berechnungen mit dieser Formel nicht effektiv. Für numerische Forschung eignen sich im Gegensatz dazu moderne Primzahltests besser. Die exakte Formel ist jedoch von theoretischem Interesse: sie birgt nämlich den Fehlerabstand zwischen der einfachen Vorhersage und der tatsächlichen Primzahlverteilung. Es wird vermutet, dass dieser Fehler (innerhalb des Spektrums aller Möglichkeiten) kleinstmöglich ist. Dabei wäre eine Entschlüsselung dieses Fehlers nicht so sehr für die Numerik von Relevanz. Vielmehr ist die reine Mathematik bestrebt, den bisher verborgenen Grund zu erfahren, weshalb der Fehler (falls zutreffend) so klein wie möglich ausfällt.
Die Primzahlen sind nicht nur Gegenstand der mathematischen Grundlagenforschung, sondern haben auch praktische Anwendungen. So kommen beispielsweise bei Kryptosystemen wie der RSA-Verschlüsselung sehr große Primzahlen zum Einsatz.
Wie „funktioniert“ die Zeta-Funktion?[Bearbeiten | Quelltext bearbeiten]
Eine mathematische Funktion ist im Grunde wie eine Rechenmaschine. Man gibt einen Wert in die Funktion ein, und diese liefert dann ein Ergebnis in Abhängigkeit vom Eingabewert, zumindest theoretisch. Damit ist gemeint, dass die Funktion an sich nicht rechnet, sondern meist nur eine Rechenvorschrift formelhaft festhält. Einfaches Beispiel für eine Funktion ist die quadratische Funktion, welche die Eingabe mit sich selbst multipliziert. Formelhaft schreibt man dies als . Somit ordnet die quadratische Funktion beispielsweise der Zahl den Wert zu. Rechnet man dies aus, ergibt sich , also .
Im Prinzip funktioniert die Riemannsche Zeta-Funktion genau wie das obere Beispiel, nur dass die Rechenvorschrift etwas komplizierter ist. Um diese zu verstehen, muss das Konzept der unendlichen Reihen bekannt sein. Eine (konvergente) Reihe ist grob gesagt eine Summe von Zahlen, die niemals endet und die sich einer Zahl immer mehr annähert. Ein elementares nicht-triviales Beispiel einer Reihe fußt auf der Zahl , die in Dezimalschreibweise nicht geschlossen, sondern nur durch die unendliche periodische Entwicklung
geschrieben werden kann. Schaut man genauer hin, sieht man, dass dies gerade die Summe aller kehrwertiger 10er-Potenzen ist:
Damit sich die unendlich lange Summe einem Wert annähert, muss gewährleistet sein, dass die Summanden „schnell genug klein“ werden.
Die Riemannsche Zeta-Funktion ist nun vergleichbar mit einer Rechenmaschine, die zu einer gegebenen Zahl die unendliche Summe der Kehrwerte aller natürlichen Potenzen mit diesem Exponenten bildet. Als mathematische Formel lautet diese Vorschrift
- .
Um das besser zu verstehen, betrachtet man das Beispiel der Eingabe . Die natürlichen Potenzen mit diesem Exponenten sind gerade die Quadratzahlen 1, 4, 9, 16, 25 … . Damit wäre das Ergebnis der Zeta-Rechenmaschine in Abhängigkeit vom Eingabewert 2 die Reihe
Es stellt sich heraus, dass die Ausdrücke schnell genug klein werden, so dass diese unendlich lange Summe sich einem gewissen Zahlenwert beliebig annähert, je weiter man summiert. Experimentell kann man festhalten:
und wenn man sogar bis zur millionsten Quadratzahl geht
Da hier bereits sehr viele Terme addiert wurden, kann man vermuten, dass dem exakten Ergebnis schon recht nahe ist. Der exakte Grenzwert ist, das konnte Leonhard Euler begründen, die Zahl
- .
Dabei ist die Kreiszahl. Zwar kannte Euler den Beginn der Dezimalfolge , doch seine Begründung beruhte letztlich auf mathematischen Argumenten und nicht expliziten Rechnungen, da die Summe ja niemals endet. Somit liefert die Zeta-Funktion für die Eingabe 2 das Ergebnis . Analog müssen für die Eingabe 3, 4 … usw. entsprechend die Kehrwerte aller Kubikzahlen, Biquadratzahlen usw. addiert werden und es kommen neue Grenzwerte , … usw. zustande.
Definition und Darstellungsformen[Bearbeiten | Quelltext bearbeiten]
Dirichlet-Reihe[Bearbeiten | Quelltext bearbeiten]
Die Zeta-Funktion wird in der Literatur oft über ihre Darstellung als Dirichlet-Reihe definiert.
Für komplexe Zahlen , deren Realteil größer als 1 ist, ist die Zeta-Funktion definiert durch die Dirichlet-Reihe[5]
Wie man mittels des Integralkriteriums für unendliche Reihen zeigen kann, ist diese Reihe im angegebenen Bereich absolut konvergent. Zudem ist die Konvergenz auf kompakten Teilmengen gleichmäßig, weshalb nach dem Satz von Weierstraß die dargestellte Funktion holomorph ist. Wegen der Divergenz der harmonischen Reihe ist diese Darstellung für alle komplexen Zahlen mit Realteil kleiner oder gleich 1 jedoch ungültig. In besonderem Maße wird dies für negative Argumente ersichtlich, wenn man zum Beispiel versuchte, die Zeta-Funktion für über die Dirichlet-Reihe auszuwerten. Man hätte dann
und diese Reihe hat offensichtlich keinen endlichen Grenzwert.
Dennoch wird die Dirichlet-Reihe aufgrund ihrer Einfachheit und ihrer zahlentheoretischen Relevanz (siehe Euler-Produkt) als Basisdefinition verwendet. Mittels analytischer Fortsetzung (siehe unten) wird eine sinnvolle Berechnung für alle komplexen Zahlen mit möglich. Damit kann schließlich auch Werten wie ein Sinn gegeben werden, es gilt zum Beispiel .
Euler-Produkt[Bearbeiten | Quelltext bearbeiten]
Eine wesentliche Eigenschaft der Zeta-Funktion ist ihre Verbindung zu den Primzahlen. Euler, der als Erster diesen Zusammenhang entdeckte, betrachtete dafür das später nach ihm benannte Euler-Produkt, das für alle mit gültig ist:[5]
Es ist genau äquivalent zur Dirichlet-Reihe und wird von manchen Autoren als Definition verwendet.[6][7] Jeder einzelne Faktor des Produktes stellt eine geometrische Reihe gebildet über den Wert dar, während sich das ganze Produkt über alle Primzahlen erstreckt. Das Euler-Produkt ist erstaunlich, weil Primzahlen aufgrund ihrer nicht genau vorhersehbaren Verteilung sehr schwer in analytischen Ausdrücken unterzubringen sind. Es stellt sich aber eine überraschend einfache Identität zwischen den „chaotischen“ Primzahlen und einer bekannten Reihe heraus.
| Für die detaillierte Herleitung |
| Für die formale Herleitung des Euler-Produktes werden lediglich die geometrische Reihe, der Satz, dass jede natürliche Zahl genau eine Zerlegung als Produkt von Primzahlen besitzt, sowie Ausmultiplizieren von Klammern benötigt. Zu Beginn bewährt es sich, nur eine endliche Anzahl von Primzahlen im Produkt zu beachten. Entwickelt man jeden Term als eine geometrische Reihe , so ergibt sich im Falle nur einer Primzahl wobei das Potenzgesetz zu beachten ist. Zur Rechten stehen genau die Zahlen, die ausschließlich Zweien in ihrer Primfaktorzerlegung haben, also die Zweierpotenzen. Verfährt man weiter mit den ersten zwei Primzahlen, ergibt sich Multipliziert man beide Klammen aus, ergeben sich in der Summe alle Kombinationen von Termen der Form mit , es gilt also und auf der rechten Seite stehen genau alle solchen Terme , sodass nur Zweien und Dreien in seiner Primfaktorzerlegung hat. Beim Ausmultiplizieren wird jeder Summand der einen Klammer mit einem Summand der anderen Klammer verrechnet, und das in jeder Kombination, für sind die entsprechenden Terme in Rot markiert. Auf ähnliche Weise findet man, dass zu der entsprechenden Dirichlet-Reihe korrespondiert, in der alle Zahlen mit Primfaktorzerlegung auftauchen, und so weiter. Entsprechend gilt für allgemein die ersten Primzahlen Nun kann man in dieser Formel gegen Unendlich laufen lassen, und erhält da jede Zahl genau eine Zerlegung besitzt. |
Das Euler-Produkt konvergiert im betrachteten Bereich unbedingt.[8] Mittels des Identitätssatzes für Dirichlet-Reihen lässt sich zeigen, dass das Euler-Produkt und der Fundamentalsatz der Arithmetik zueinander äquivalent sind. Daher wird es zuweilen auch als dessen analytische Version bezeichnet.[9] Eine wichtige Folgerung des Euler-Produktes für die Analysis der Zeta-Funktion ist, dass für alle gilt. Dies ist eine Konsequenz einer Erweiterung des Satzes vom Nullprodukt für unendliche Produkte: keiner der Faktoren des Euler-Produktes ist für irgendeinen Eingabewert aus diesem Bereich Null, also wird es auch nicht im Grenzwert Null sein.[10] Weitaus nichttrivialer ist die Tatsache, dass das Euler-Produkt, im Gegensatz zur Dirichlet-Reihe, auch auf der Geraden , mit Ausnahme von , an Gültigkeit behält. Es gilt[11]
was die Nullstellenfreiheit von im gesamten Bereich zur Folge hat. Als eine Folgerung der Funktionalgleichung ergibt sich, dass die einzigen Nullstellen von außerhalb des sog. kritischen Streifens die trivialen Nullstellen
sind. Alle anderen Nullstellen bezeichnet man als nichttrivial, und diese liegen allesamt im kritischen Streifen.[12]
Mithilfe des Euler-Produkts der Zeta-Funktion kann ein Beweis des Satzes von Euklid mit analytischen Methoden angegeben werden. Der Satz von Euklid besagt, dass es unendlich viele Primzahlen geben muss, und wurde etwa 300 Jahre vor Christus durch Euklid von Alexandria bewiesen. Unter der Annahme, es gäbe nur endlich viele Primzahlen, gilt
was ein Widerspruch zur Divergenz der harmonischen Reihe ist. Ähnlich bemerkenswert ist die Argumentation über die Formel
Bei endlich vielen Primzahlen wäre die linke Seite eine rationale Zahl, die rechte Seite ist aber aufgrund der Transzendenz der Kreiszahl irrational.[13]
Eine weitere direkte Folgerung des Euler-Produktes, durch Logarithmieren und anschließende Verwendung der Taylor-Reihe des Logarithmus, ist die für gültige Formel
wobei mit die Primzetafunktion bezeichnet.[14] Mit Hilfe von Möbius-Inversion lässt sich daraus eine Möglichkeit ableiten, die Primzetafunktion schnell aus einer Reihe über logarithmierte Zeta-Funktionen zu gewinnen:[15]
Unter anderem kann dieser Ausdruck für eine schnelle numerische Berechnung der Primzetafunktion herangezogen werden.[16] Ferner folgt aus für , dass die Reihe der reziproken Primzahlen divergiert.
Mellin-Transformation[Bearbeiten | Quelltext bearbeiten]
Die nach der Definition als Dirichlet-Reihe und dem Euler-Produkt wohl elementarste und wichtigste Darstellung der Zeta-Funktion ist die mit Hilfe eines uneigentlichen Integral-Ausdrucks. Auch diese Darstellung geht direkt aus der Dirichlet-Reihe hervor.
Grundlage dieser Darstellung ist die eulersche Integral-Darstellung der Gamma-Funktion
aus dem nach der Substitution mit und Division durch nach beidseitigem Summieren der Ausdruck
hervorgeht.[17] Diese Darstellung von gilt naturgemäß nur auf der Halbebene . Die zweite Integraldarstellung von bezeichnet man auch als die Mellin-Transformation von . Das mögliche Vertauschen von Summe und Integral kann mit absoluter Konvergenz und dem Satz von Lebesgue begründet werden. Eine dazu verwandte Form ist
mit der Jacobischen Theta-Funktion (eine Modulform halbganzen Gewichts).
Die Darstellung der Zeta-Funktion mit Hilfe der Gamma-Funktion und der Mellin-Transformation von ist daher zentral, da sie ein Ausgangspunkt für die analytische Fortsetzung der Zeta-Funktion ist. Außerdem können mit ihr charakteristische Funktionalgleichungen und die Beziehung zur Theorie der Modulformen hergeleitet werden.
Methoden zur analytischen Fortsetzung[Bearbeiten | Quelltext bearbeiten]
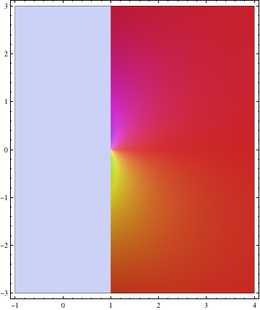
−1 < Re(s) < 4 und −3 < Im(s) < 3 mit Kolorierung der Funktionswerte: Dirichlet-Reihe, Euler-Produkt und Mellin-Transformation konvergieren nur auf der um 1 verschobenen rechten Halbebene. Sie können die Zeta-Funktion im grau gefärbten Bereich nicht darstellen.

Die anfänglich nur für komplexe Zahlen definierte Zeta-Funktion kann zu einer in ganz holomorphen Funktion ausgeweitet werden. Diese Tatsache mag zunächst ungewöhnlich wirken, da ihre Dirichlet-Reihe an vielen Stellen nicht mehr konvergiert. Tatsächlich aber steht die Dirichlet-Reihe (wie auch Euler-Produkt und Mellin-Transformation aus Gründen der Äquivalenz) nicht überall für die Definition der Zeta-Funktion zur Verfügung.
An der Stelle besitzt die Zeta-Funktion zunächst mit Sicherheit eine Definitionslücke, denn mit der Divergenz der harmonischen Reihe folgt
Also wird sie in jedem Intervall beliebig anwachsen. Diese Lücke bildet gleichzeitig eine natürliche Barriere für die Konvergenz der Dirichlet-Reihe, was aus den Regeln für Abszissen von Dirichlet-Reihen folgt, denn die betrachtete Dirichlet-Reihe hat Konvergenzabszisse .
Eine analytische Fortsetzung der im Gebiet durch die Reihe definierten holomorphen Funktion ist eine auf einem größeren Gebiet holomorphe Funktion, die auf ganz mit dieser übereinstimmt. Nach dem Identitätssatz für holomorphe Funktionen ist eine solche Fortsetzung stets eindeutig bestimmt. Damit sind alle Werte der Zeta-Funktion im erweiterten Bereich bereits durch die Dirichlet-Reihe festgelegt, obwohl sie hier nicht mehr an allen Stellen konvergiert.
Umformungen der Dirichlet-Reihe und die Eulersche Reihentransformation[Bearbeiten | Quelltext bearbeiten]
Obwohl es für den ganz allgemeinen Fall kein konstruktives Verfahren gibt, Berechnungsformeln für analytische Fortsetzungen anzugeben, ist es durch die Einfachheit der Dirichlet-Reihe nicht schwierig, für die Zeta-Funktion eine zu finden. Besonders einfach erweist sich dies für die gelochte Halbebene
mittels folgender Beobachtung:[18]
Die Reihe zur Rechten konvergiert nachweislich in der Halbebene gegen eine holomorphe Funktion und wird in der Literatur auch manchmal als Dirichletsche Etafunktion bezeichnet. Damit lässt sich die Zeta-Funktion zu einer in ganz holomorphen Funktion fortsetzen. Die Lücke in wird mittels des Faktors gehoben und muss daher ein Pol erster Ordnung sein. Das Residuum der Zeta-Funktion ist dort 1, das heißt, es gilt:[19]
Alle Stellen mit sind hingegen hebbare Singularitäten, denn es gilt dann Dies zeigt man am besten mittels partieller Summation: Für alle gilt[20]
Für eine weitere holomorphe Ausdehnung des Definitionsbereiches eignen sich nun viele Methoden, die jedoch nach dem Identitätssatz alle dieselbe Funktion darstellen. Eine davon bietet die Anwendung der Eulerschen Reihentransformation auf die obere alternierende Reihe. Man erhält damit eine von Konrad Knopp veröffentlichte und auf ganz definierte Reihenidentität
Diese wurde 1930 von Helmut Hasse bewiesen.[21] Es treten daher während der weiteren Fortsetzung keine weiteren Lücken bzw. Pole mehr auf. Daraus folgt schließlich Holomorphie in .
Durch Limitierungsverfahren[Bearbeiten | Quelltext bearbeiten]
Die Idee der Theorie der Limitierungsverfahren ist es, einem divergenten Grenzprozess einen endlichen Wert zuzuordnen, indem man etwa zusätzliche Parameter einführt, die man anschließend gegen den Ursprungsausdruck „limitiert“. Dies geht bereits auf Leonhard Euler zurück, der berühmt für seinen sorglosen Umgang mit divergenten Reihen ist. Er berechnete einige Werte der Zeta-Funktion annähernd auch außerhalb des Bereichs, in welchem die Dirichlet-Reihe konvergiert. Auf diese Weise stieß er auch auf seine Vermutung hinsichtlich der Gültigkeit ihrer Funktionalgleichung, die er allerdings nicht beweisen konnte.
Der Gedanke ist, der für divergenten Reihe
für alle Werte einen „Grenzwert“ zuzuordnen. Dies gelingt durch Einführen eines weiteren Parameters . Es ist die Reihe
für jedes für alle konvergent. Auf dieser Basis kann der Konvergenzbegriff abgeschwächt werden: Eine Reihe heißt A-summierbar, falls die zugehörige Potenzreihe für alle konvergiert und der Grenzwert existiert.[22] Ist eine Reihe bereits im klassischen Sinne konvergent, stimmen die jeweiligen Grenzwerte nach dem Abelschen Grenzwertsatz überein, doch es gibt A-summierbare Reihen, die nicht konvergieren. Es ist also A-Summierbarkeit eine wohldefinierte Verallgemeinerung der klassischen Reihenkonvergenz. Durch Bilden des Grenzwertes , d. h., nähert sich von links, erhält man
sogar für alle , und die rechte Seite stellt eine ganze Funktion dar.[23]

Durch die Hinzunahme einer zweiten zu limitierenden Variable entsteht zugleich eine Beziehung zum Polylogarithmus. Dieser verallgemeinert unter anderen den natürlichen Logarithmus und ist für gegeben durch die Potenzreihe
Ist zudem , so ist diese Reihe auch an den Randwerten (außer bei ) konvergent. Generell ist für feste Werte eine analytische Fortsetzung in auf das Gebiet möglich. Es gilt für alle die Beziehung , aber auch
für Werte . Etwa für gilt zunächst für (siehe Bild rechts), also nach Grenzwertbildung
Die Euler-Maclaurin-Summenformel[Bearbeiten | Quelltext bearbeiten]
Eine weitere Möglichkeit, eine analytische Fortsetzung anzugeben, bietet die Euler-Maclaurin-Summenformel. Diese drückt diskrete Summen explizit in der Sprache der Integralrechnung aus und ist allgemein gegeben durch
Hierbei ist eine auf dem Intervall mindestens -mal differenzierbare Funktion und eine natürliche Zahl. Es bezeichnen zudem die Bernoulli-Polynome und den ganzzahligen Anteil von .[24]
Mit , und folgt also[25]
Dabei ist das Restglied gegeben durch[25]
und konvergiert in der gesamten Halbebene (gleichmäßig auf kompakten Teilmengen). Daher stellt diese Formel eine holomorphe Fortsetzung der Zeta-Funktion in die Halbebene dar. Lässt man gegen unendlich gehen, ergibt sich damit ein holomorpher Ausdruck für ganz .[26]
Setzt man zum Beispiel , ergibt sich die in der Literatur häufig zitierte Darstellung
die für gültig ist.[27]

Integration über eine Hankel-Kontur[Bearbeiten | Quelltext bearbeiten]
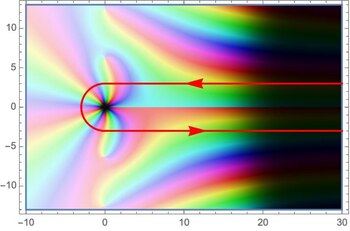
Eng verwandt mit der Darstellung der Zeta-Funktion mittels der Mellin-Transformation ist eine Darstellung der Funktion mittels eines Kurvenintegrals. Diese wurde von Riemann selbst verwendet, um die Zeta-Funktion in die komplexe Ebene fortzusetzen. Die Funktion ist je nach Wahl des Zweiges des Logarithmus in unterschiedlichen Bereichen holomorph. Für die Hankel-Kontur (einen speziellen Integrationsweg) ist es von Vorteil, die Gerade aus dem Gebiet auszuschließen via:
Nun definiert man für die Funktion als ein Kurvenintegral über . Die gewählte Kurve kommt von , verläuft mit Abstand über der reellen Geraden, umläuft den Ursprung in einem Halbkreis und erstreckt sich dann wieder mit Abstand unterhalb der reellen Geraden gegen :
Wegen gleichmäßiger Konvergenz auf kompakten Mengen in ist eine ganze Funktion. Wählt man nun , so kann man wegen die Schlaufe beliebig zusammenziehen und erhält mit der Mellin-Transformation
Daraus ergibt sich mit dem Ergänzungssatz die Formel[28]
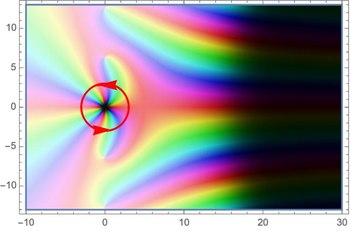
Ist , so ist innerhalb des gelochten Streifens holomorph. Damit lässt sich die Hankel-Kontur zu einer Kreiskurve zusammenziehen, ohne den Wert des Integrals zu verändern. Dies ermöglicht eine schnelle Berechnung der Werte für ganze Zahlen mittels des Residuensatzes. Unter anderem folgt daraus
für alle und die enge Beziehung der Werte der Zeta-Funktion an nicht-positiven ganzen Argumenten und den Bernoulli-Zahlen.
Diese Darstellungsform kann auch zu einer direkten Herleitung der Funktionalgleichung verwendet werden. Dabei wird die Kurve modifiziert und es kommt der Residuensatz zum Einsatz.[29]
Weitere Darstellungsmöglichkeiten[Bearbeiten | Quelltext bearbeiten]
Erwähnenswert ist der Reihenausdruck
- ,
der für alle Werte definiert ist.[30] Interessant daran ist, dass sich damit die Zeta-Funktion rekursiv auf die ganze Zahlenebene fortsetzen lässt, da für die Berechnung von lediglich die Werte benötigt werden.
Von Helmut Hasse stammt die global konvergente Reihe[31]
Ein exotischer und global konvergenter Ausdruck ergibt sich, wenn man direkt die elementare Reihendarstellung der Zeta-Funktion in die Abel-Plana-Summenformel einsetzt:[32]
Geschichte[Bearbeiten | Quelltext bearbeiten]
Im Gegensatz zu den Primzahlen oder der euklidischen Geometrie ist die mathematische Entdeckungsgeschichte der Riemannschen Zeta-Funktion sehr jung. So sind alle bis heute wesentlichen Entdeckungen zu dieser Funktion in den letzten 250 Jahren gemacht worden. Auf der einen Seite lässt sich die im Verhältnis zur Entstehung einer rigorosen (komplexen) Analysis frühe Entdeckung mit der Einfachheit der Reihe begründen. Auf der anderen Seite lassen sich die späten Resultate mit der Schwierigkeit von deren Eigenschaften erklären.
Um 1735 löste Leonhard Euler das Basler Problem[Bearbeiten | Quelltext bearbeiten]


Einer der ersten Mathematiker, der sich mit einem Vorläufer der wie heute definierten Zeta-Funktion intensiv und ausführlich auseinandersetzte, war Leonhard Euler. Seit Mitte des 17. Jahrhunderts versuchten Mathematiker, den exakten Grenzwert der unendlichen Reihe
zu bestimmen. Persönlichkeiten wie Pietro Mengoli, der das Basler Problem (wie es später bezeichnet wurde) erstmals formulierte, aber auch Jakob I Bernoulli scheiterten mit ihren Lösungsversuchen. Erst um das Jahr 1734 fand Leonhard Euler die Lösung
mit der Kreiszahl , indem er eine neuartige Technik zur Berechnung der Sinusfunktion entwickelte.[33] Dieser Beweis wurde jedoch nach Veröffentlichung von seinen Zeitgenossen zunächst nicht akzeptiert. Daraufhin konterte er mit der Veröffentlichung eines alternativen Beweises im Jahr 1741.[34] Natürlicherweise war Euler bald darauf an der Untersuchung von Reihen des Typs
interessiert. Er hatte die Hoffnung, weitere und außerdem weit bedeutendere Aussagen treffen zu können. Und tatsächlich sollte es nicht nur bei der Lösung des Basler Problems bleiben. Er fand unter anderem die Formeln
die 1735 in seiner Arbeit De Summis Serierum Reciprocarum erstmals veröffentlicht wurden. Obwohl mit steigenden Eingabezahlen die Funktionswerte komplizierter werden, berechnete Euler von Hand[35] den Wert
In seinem Buch Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum, das 1755 veröffentlicht wurde, bewies er schließlich eine allgemeine Formel für .[36] Diese zeigte auf, dass sich tatsächlich jedes stets als ein rationales Vielfaches der Potenz schreiben lässt. Nicht erfolgreich war er hingegen bei ungeraden Argumenten, also zum Beispiel bei der Reihe
da sich hier keine seiner Techniken anwenden ließ. Jedoch berechnete er die Werte für bis auf mehrere Dezimalstellen. Außerdem schrieb er einheitlich , wobei im Falle, dass eine gerade Zahl ist, rational ist. Für den Fall, dass ungerade ist, vermutete Euler, sei „eine Funktion von “.[37] Dies konnte jedoch, ungeachtet der vagen Formulierung Eulers, bis heute nicht bestätigt werden. Die Werte der Reihen für ungerade Argumente größer als 1 sind bis heute (Stand 2020) weitestgehend unbekannt und Gegenstand zahlentheoretischer Vermutungen.[38]
Euler gilt als Entdecker der Verbindung zwischen der Zeta-Funktion und den Primzahlen. Diese Verknüpfung wird bis heute als Euler-Produkt bezeichnet. So schrieb er in seiner Arbeit Variae observationes circa series infinitas:
„Wenn aus der Reihe der Primzahlen der folgende Ausdruck gebildet wird wird sein Wert der Summe dieser Reihe gleich sein “
Sofort war sich Euler der Beziehung zwischen den Primzahlen und der Geometrie bewusst, und er schrieb weiter:
„Weil nach Setzen von gilt , wobei die Peripherie des Kreises bezeichnet, dessen Durchmesser 1 ist, wird sein “
Aus der schon damals gut bekannten Tatsache, dass die harmonische Reihe divergent ist, konnte Euler ebenfalls aus dem Euler-Produkt schließen, dass die Summe der Kehrwerte aller Primzahlen keinen endlichen Grenzwert hat.[41] Bezeichnet wird dieses Resultat auch als Satz von Euler über die Summation der Kehrwerte der Primzahlen.
Auch war die von Riemann später bewiesene Funktionalgleichung bereits Euler bekannt. In seiner Arbeit Remarques sur un beau rapport entre les series des puissances tant directes que reciproques beschrieb er diese mathematisch nicht rigoros:[42]
„Par cette raison je hazarderai la conjecture suivante, que quelque soit l’exposant n, cette équation ait toujours lieu:
- “
„Aus diesem Grund wage ich die folgende Vermutung vorzuschlagen, dass für jede Variable n die folgende die Gleichung immer gültig ist:
- “
Dabei bezog sich Euler eigentlich auf die Dirichletsche Etafunktion, die jedoch bis auf einen Faktor der Riemannschen Zeta-Funktion entspricht. Euler gab keinen rigorosen Beweis einer Funktionalgleichung, sondern hatte diese nur für viele Werte überprüft und anschließend als universell gültig vermutet.
Dirichlet zeigt seinen Primzahlsatz[Bearbeiten | Quelltext bearbeiten]

Im Jahre 1838 gelang dem Mathematiker Peter Dirichlet ein großer Beitrag zur Zahlentheorie. Er bewies eine Vermutung von Fermat, die nun Dirichletscher Primzahlsatz heißt. Diese besagt, dass jede arithmetische Progression mit positiven, teilerfremden unendlich viele Primzahlen enthält.[44] Ist hier zum Beispiel und , folgt, dass die Liste 1, 5, 9, 13, 17 … unendlich viele Primzahlen beinhaltet.
Schlüssel zum Beweis waren neben der Riemannschen Zeta-Funktion eine ganze Klasse weiterer Funktionen, die ebenfalls in Primzahlprodukte zerfallen und somit eine „große Familie“ bilden. Erst ein Jahrhundert später konnten dank feinerer Methoden die Ergebnisse von Dirichlet durch Siegel und Walfisz deutlich präzisiert werden (Satz von Siegel-Walfisz).
Riemanns Beitrag zur Zeta-Funktion[Bearbeiten | Quelltext bearbeiten]

Im Jahr 1859 arbeitete Bernhard Riemann in seiner Publikation Über die Anzahl der Primzahlen unter einer gegebenen Größe den bereits von Euler gegebenen Zusammenhang der Zeta-Funktion zu den Primzahlen entscheidend aus. Die große Leistung bestand darin, die Relevanz der Ausweitung des Definitionsbereichs auf komplexe Zahlen zu erkennen. Erst mit dieser Herangehensweise war es möglich geworden, konkrete Informationen über Primzahlen 2, 3, 5, 7 … selbst zu gewinnen. Das ist insofern bemerkenswert, als Primzahlen reelle Zahlen sind. Riemann, der ein Schüler von Carl Friedrich Gauß war, schrieb in seiner zehnseitigen Arbeit eine funktionentheoretische Interpretation und Auswertung des Euler-Produkts, die einen Zusammenhang zwischen Primzahlen und den nicht-trivialen Nullstellen der Zeta-Funktion schaffte. Das Hauptresultat war eine Formel, die ohne jeden Fehler die Anzahl der Primzahlen unter einer gegebenen (nicht ganzen) positiven Zahl abzählte. Damit war ihm ein völlig neuer Zugang zur Theorie der Primzahlen gelungen.
Er etablierte in seiner Arbeit das griechische (Zeta) als Funktionssymbol und formulierte außerdem die bis heute unbewiesene nach ihm benannte Riemannsche Vermutung, die eine wichtige Aussage über die genaue Lage der Nullstellen der Zeta-Funktion behauptet.

Obwohl der Artikel heutzutage als Durch- und Aufbruch zur modernen analytischen Theorie um die Zeta-Funktion gesehen wird, stieß er damals in Mathematikerkreisen bei Weitem nicht nur auf Begeisterung. Schuld daran war in erster Linie, dass Riemann es an den meisten Stellen unterlassen hatte, Beweise für seine aufgestellten Formeln zu hinterlegen. So kam es, dass Godfrey Harold Hardy und John Edensor Littlewood Riemanns Arbeit lediglich als „beachtliche Ansammlung heuristischer Einsichten“ bezeichneten,[45] die englischen Mathematiker waren allerdings in der analytischen Zahlentheorie zu Beginn des 20. Jahrhunderts anfangs noch so rückständig, dass Littlewood sich erinnerte, die Riemannsche Vermutung 1906 von seinem Professor als Übungsaufgabe gestellt bekommen zu haben. Auch Edmund Landau gehörte zu den lautesten Kritikern hinsichtlich der Bedeutung des Artikels. Zwar nannte er ihn zunächst „brillant und fruchtbar“, jedoch schlug sein Lob bald um:
„Riemanns Formel ist bei weitem nicht das wichtigste in der Theorie der Primzahlen. Er schuf einige Hilfsmittel, die, wenn sie erstmal ausgearbeitet sind, manche anderen Beweise ermöglichen werden.“
Detlef Laugwitz bemerkt dazu in seiner Riemann-Biographie, dass Landau auch Eulers bahnbrechende Arbeiten in seinen Lehrbüchern wenig würdigte, da er tendenziell nur Arbeiten schätzte, in denen jedes Detail ausgearbeitet war.[47] Auf der anderen Seite bewunderten Mathematiker wie Felix Klein, Riemann habe „mit großen allgemeinen Ideen“ gearbeitet und „oft auf seine Intuition“ vertraut.[48] Das war noch bevor Carl Ludwig Siegel durch das Studium des Nachlasses zeigte, wie umfangreich Riemanns analytische Arbeiten zur Zeta-Funktion waren. Die Rechnungen im Nachlass waren allerdings schwer zu entschlüsseln und es bedurfte eines Mathematikers vom Kaliber Siegels, die Ideen Riemanns zu rekonstruieren.
Riemann arbeitete seit dieser Zeit bis zu seinem frühen Tode (er starb mit gerade mal 39 Jahren an den Folgen einer Tuberkulose) nicht mehr an der Zeta-Funktion, es blieb seine einzige Veröffentlichung zur Zahlentheorie.[49] Der Aufsatz von 1859 war nur skizzenhaft ausgeführt, Riemann wollte sich damit für die Aufnahme in die Berliner Akademie der Wissenschaften bedanken.
Viele von Riemanns Aufzeichnungen wurden nach seinem Ableben von seiner Haushälterin verbrannt, bis sie von Mitarbeitern der Göttinger Fakultät gestoppt wurde. Die verbliebenen Schriften wurden seiner Witwe übergeben und verschwanden damit für viele Jahre. Über weitere Resultate zur Zeta-Funktion, die man ohne teilweise Vernichtung der Dokumente gefunden hätte, kann bis heute nur noch spekuliert werden.
Die letzten Jahre des 19. Jahrhunderts[Bearbeiten | Quelltext bearbeiten]
Mangoldt beweist die Hauptformel von Riemann[Bearbeiten | Quelltext bearbeiten]
Im Jahr 1893 publizierte der Mathematiker Jacques Hadamard eine Arbeit, in welcher der Grundstein eines detaillierteren Verständnisses von Riemanns Arbeit gelegt wurde. Hadamard war es gelungen, eine Formel für die Zeta-Funktion zu beweisen, die ihre Nullstellen beinhaltet. Genau genommen handelte es sich dabei um ein Verfahren, die Zeta-Funktion als Ganzes aus ihren Nullstellen zu konstruieren. Die Existenz einer solchen Formel wurde von Riemann bereits vorausgesetzt, war jedoch bis dato nicht rigoros bewiesen worden. Für die Verifikation der Riemannschen Ideen war sie aber ein substanzieller Teil: das Grundschema der Argumentation für Riemanns Hauptformel lautete nämlich „Primzahlprodukt (Euler) versus Nullstellenprodukt (Riemann/Hadamard)“. Unter anderem deshalb bezeichnete Hans von Mangoldt den Beitrag von Hadamard „als ersten wirklichen Fortschritt in diesem Gebiet seit 34 Jahren“.[50][51]
Aufbauend auf der Arbeit von Hadamard gelang Hans von Mangoldt nur zwei Jahre später, im Jahre 1895, der Durchbruch zu Riemanns Hauptformel.[52] Allerdings zeigte er diese in einer leicht veränderten Version, die heute als „natürlicher“[53] angesehen wird. Seiner Leistung zu Ehren wird die Hauptformel heute als Riemann-von-Mangoldt-Formel bezeichnet.
Hadamard und De La Vallee-Poussin beweisen den Primzahlsatz[Bearbeiten | Quelltext bearbeiten]
Nachdem von Mangoldt im Jahr 1895 den Beweis der Riemannschen Hauptformel erbracht hatte, fehlte zum Beweis des Primzahlsatzes nicht mehr viel. Dieser Satz trifft eine Aussage darüber, wie häufig Primzahlen durchschnittlich auftauchen. Es blieb lediglich zu zeigen, dass die Zeta-Funktion keine Nullstellen in dem Bereich hat, in dem das Primzahlprodukt von Euler „gerade so nicht mehr gültig ist“. Unabhängig voneinander erbrachten Hadamard und der Belgier Charles-Jean de La Vallée Poussin den Beweis im Jahr 1896.[54] Wichtige Punkte für den Beweis waren Ideen von Franz Mertens und die trigonometrische Identität .[55]
Obwohl die Aufregung in der Mathematikerwelt groß war, gab es bezüglich der Beweismethode, die stark an die Eigenschaften der schwierigen Zeta-Funktion gebunden war, Bedenken über deren Natürlichkeit. Es wurde als seltsam erachtet, dass eine Aussage über Primzahlen sogar äquivalent zu einer gewissen Verteilung der Nullstellen einer komplexen Funktion war. So äußerte Albert Ingham 1932:
„Man kann den Beweis des Primzahlsatzes, […] von de la Vallée Poussin und Hadamard für unbefriedigend halten, denn es werden Begriffe eingeführt, die sehr weit vom ursprünglichen Problem entfernt sind. Deswegen ist es nur allzu natürlich, nach einem Beweis zu fragen, der nicht von der Theorie der Funktionen einer komplexen Veränderlichen abhängt. Hierauf müssen wir antworten, daß gegenwärtig kein derartiger Beweis bekannt ist. Wir können in der Tat weiter gehen und sagen, daß es unwahrscheinlich ist, dass ein wahrhaft reeller Beweis gefunden wird; zumindest ist das so lange unwahrscheinlich, wie sich die Theorie auf die Eulersche Identität stützt. Denn jeder bekannte Beweis des Primzahlsatzes stützt sich auf eine gewisse Eigenschaft der komplexen Nullstellen von und umgekehrt ist diese Eigenschaft eine einfache Folgerung des Primzahlsatzes selbst. Es scheint deswegen klar zu sein, daß diese Eigenschaft explizit oder implizit in jedem Beweis verwendet werden muss, der auf beruht, und man erkennt nicht, wie ein Beweis geführt werden soll, wenn man lediglich die reellen Werte von verwendet.“
Im Jahr 1948 wurde schließlich ein elementarer (also gänzlich ohne funktionentheoretische Mittel auskommender) Beweis von Atle Selberg und Paul Erdös gegeben.[58] Hierbei bedeutet „elementar“ jedoch keinesfalls „einfach“.[59] Es wurden im Lauf der Zeit auch erheblich einfachere funktionentheoretische und elementare[60] Beweise des Primzahlsatzes gefunden.
Anfang des 20. Jahrhunderts[Bearbeiten | Quelltext bearbeiten]
Hilbert formuliert seine 23 Probleme[Bearbeiten | Quelltext bearbeiten]

Im Rahmen des 2. Internationalen Mathematikerkongresses des Jahres 1900 in Paris hielt David Hilbert am 8. August einen Vortrag. In diesem formulierte er eine Liste von 23 mathematischen Problemen, die seiner Ansicht nach zu den wichtigsten des kommenden Jahrhunderts zählten. Hilbert zählte zu diesem Zeitpunkt bereits zu den führenden Mathematikern der Gegenwart. Problem Nr. 8 war die Riemannsche Vermutung:
„In der Theorie der Verteilung der Primzahlen sind in neuerer Zeit durch Hadamard, De La Vallee-Poussin, V. Mangoldt und andere wesentliche Fortschritte gemacht worden. Zur vollständigen Lösung der Probleme, die uns die Riemannsche Abhandlung "Über die Anzahl der Primzahlen unter einer gegebenen Größe" gestellt hat, ist es jedoch noch nötig, die Richtigkeit der äußerst wichtigen Behauptung von Riemann nachzuweisen, daß die Nullstellen der Funktion , die durch die Reihe dargestellt wird, sämtliche den reellen Bestandteil haben – wenn man von den bekannten negativ ganzzahligen Nullstellen absieht. Sobald dieser Nachweis gelungen ist, so würde die weitere Aufgabe darin bestehen, die Riemannsche unendliche Reihe für die Anzahl der Primzahlen genauer zu prüfen und insbesondere zu entscheiden, ob die Differenz zwischen der Anzahl der Primzahlen unterhalb einer Größe und dem Integrallogarithmus von in der Tat von nicht höherer als der ten Ordnung in unendlich wird, und ferner, ob dann die von den ersten komplexen Nullstellen der Funktion abhängenden Glieder der Riemannschen Formel wirklich die stellenweise Verdichtung der Primzahlen bedingen, welche man bei den Zählungen der Primzahlen bemerkt hat.“
Das hohe Ansehen, das Hilbert genoss, beflügelte die Mathematiker, sich mit seinen Problemen, darunter der Zeta-Funktion, auseinanderzusetzen. Bis heute gelten 15 der 23 Probleme als gelöst, jedoch nicht die Riemannsche Vermutung.[62]
Ramanujans Arbeit zur Zeta-Funktion[Bearbeiten | Quelltext bearbeiten]


Im Jahre 1910 veröffentlichte der indische Mathematiker Srinivasa Ramanujan im Journal of the Indian Mathematical Society einen Artikel, in dem unter anderem die folgende Gleichung behauptet wurde:
Die meisten Mathematiker, die diese Gleichung zu Gesicht bekamen, hatten sie als offensichtlichen Schwachsinn gewertet. So kam es, dass Professor Hill vom University College in London schrieb:
„Mr. Ramanujan ist ein Opfer der Fallstricke des sehr schwierigen Gebietes der divergenten Reihen geworden.“
Hill verhielt sich jedoch nicht völlig ablehnend und ermutigte Ramanujan, es weiter zu versuchen. Und so schickte dieser seine Ergebnisse direkt an einige Mathematiker in Cambridge. Zwei davon waren nicht in der Lage, die Aussagen hinter Ramanujans verschlüsselten Formeln zu erkennen, und lehnten die Bitte um Unterstützung ab. Als Ramanujan jedoch schließlich auch Godfrey Harold Hardy brieflich auf seine Ideen aufmerksam machte, wurde diesem in der Gleichung die korrekte Auswertung des Werts bewusst, auch wenn sie bezüglich ihrer mathematischen Formalität natürlich inkorrekt war. In diesem Zusammenhang war die Formel schon Euler bekannt, da sie sich aus und der Funktionalgleichung ergibt (beides von Euler gefunden). Ferner erweckte Ramanujans Behauptung, eine Formel zu besitzen, die fast fehlerfrei voraussage, ob eine gegebene Zahl prim sei oder nicht (Ramanujans Formel verwendete jedoch nicht die Nullstellen der Zeta-Funktion[63]), viel Neugier. Auch in einem zweiten Brief gab er jedoch dazu keinen Beweis. Littlewood äußerte:
„Dieser Brief konnte einen rasend machen.“
Der anfänglich ausschließlich schriftliche Austausch gipfelte schließlich in einem Aufenthalt Ramanujans in England, wo sich das Duo aus Ramanujan und Hardy zu einer der produktivsten und außergewöhnlichsten mathematischen Korrespondenzen der Geschichte entwickelte.[65]
Unter anderem nach Auswertung der Tagebücher Ramanujans durch George E. Andrews und Bruce Berndt offenbarten sich die zahlreichen Ideen Ramanujans zur Riemannschen Zeta-Funktion. So fand dieser unabhängig Eulers Formel für ,[66] das Euler-Produkt[67] sowie zahlreiche unendliche Reihen und Integrale, die Zeta-Werte an ganzen und auch halbzahligen[68] Stellen beinhalten.[69][70][71]
Der Nachlass Riemanns[Bearbeiten | Quelltext bearbeiten]

Fünfzig Jahre nach Riemanns Tod tauchten einige nicht verbrannte Seiten wieder auf. Richard Dedekind, ein Kollege von Riemann hatte einige Seiten des Nachlasses von Riemanns Frau Elise erhalten und einige davon in der Bibliothek von Göttingen hinterlegt. Nachdem der Mathematikhistoriker Erich Bessel-Hagen 1926[72] die Schriften fand und beim Versuch einer Entschlüsselung der wirren Aufzeichnungen keinen Erfolg hatte, gingen die Dokumente an Carl Ludwig Siegel. Dieser war erstaunt von der Tiefe der Gedanken Riemanns bezüglich der Zeta-Funktion.[73] Dies entkräftete zugleich viel Kritik an Riemanns Originalarbeit, da die Notizen zeigten, dass Riemanns Behauptungen auf gründlichen Rechnungen beruhten.[74] Jedoch beklagte auch Siegel das Chaos in den Notizen:
„Nichts von dem, was Riemann über die Zeta-Funktion aufgeschrieben hatte, war reif für eine Veröffentlichung. Manchmal findet man unzusammenhängende Formeln auf derselben Seite, oft nur die Hälfte einer Gleichung.“
Siegel kam dahinter, dass Riemann ausschließlich über handschriftliche Rechnungen mindestens drei nicht-triviale Nullstellen der Zeta-Funktion relativ genau berechnet hatte. Die dafür verwendete Formel wurde durch Siegel ausgearbeitet, 1932 publiziert und wird seitdem auch Riemann-Siegel-Formel genannt.[76]
Nach 1945 bis heute[Bearbeiten | Quelltext bearbeiten]
Im Zeitalter des Computers[Bearbeiten | Quelltext bearbeiten]
In der Forschung rund um die Riemannsche Zeta-Funktion werden Computer vor allem dazu benutzt, die Korrektheit der Riemannschen Vermutung für möglichst viele Nullstellen zu überprüfen. Obwohl es sich bei allen Rechnungen um numerische Verfahren handelt, zeigen diese exakt und nicht nur annähernd, dass sich die untersuchten Nullstellen auf der kritischen Geraden befinden.[77][78]
Bereits im Jahr 1936 hatte der in Oxford wirkende Mathematiker Edward Charles Titchmarsh mit einer Maschine, die ursprünglich für astronomische Berechnungen konstruiert worden war, die ersten 1.041 nicht-trivialen Nullstellen der Zeta-Funktion berechnet.[79] Im Jahr 1953 wurden diese Berechnungen von Alan Turing fortgesetzt. Seine Methode wird bis heute benutzt. Erstmals kam dabei ein Computer zum Einsatz.[80][81]
Ab Beginn der 80er Jahre wurden die Computer immer leistungsstärker. Bereits im Jahr 1979 hatte eine Gruppe aus Amsterdam um Herman te Riele und Richard P. Brent 200 Millionen Nullstellen überprüft (etwas später erhöhten sie ihre Rechnung auf 300 Millionen) – alle lagen auf der kritischen Geraden. Damit widersprachen sie einer Vorhersage von Don Zagier, der geäußert hatte, es sei „ein Wunder“, falls diese immer noch ausnahmslos auf der kritischen Geraden lägen.[82] Zagier berief sich dabei auf theoretische Gründe, die zwar die Lage der ersten paar Tausend Nullstellen auf der Geraden bekräftigten, jedoch für steigende Zahlen schwächer – und letztlich sogar dagegen sprechend – auszulegen waren.
Bis 2005 wurden im Rahmen des sog. ZetaGrid Project durch verteilte Rechner die ersten 900 Milliarden Nullstellen überprüft. Um dieselbe Zeit berechnete Xavier Gourdon mit Unterstützung von Patrick Demichel die ersten 10 Billionen () Nullstellen.[83][84] Alle lagen auf der kritischen Geraden.
Zahlentheorie trifft Quantenphysik[Bearbeiten | Quelltext bearbeiten]


Im Jahr 1972 offenbarte sich durch ein zufälliges Gespräch zwischen dem Physiker Freeman Dyson und dem Mathematiker Hugh Montgomery ein bis dahin unbemerkter Zusammenhang zwischen Quantenphysik und Zahlentheorie. Gegenstand der Diskussion waren die Nullstellen der Riemannschen Zeta-Funktion. In deren von Montgomery vermuteten Verteilung erkannte Dyson die Abstände zwischen Paaren von Eigenwerten von Hermitschen Zufallsmatrizen wieder. Diese werden von Quantenphysikern zur Vorhersage der Energieniveaus in einem schweren Atomkern verwendet, wenn dieser mit nieder-energetischen Neutronen bestrahlt wird. Als Montgomery sich die Abstände zwischen den Energieniveaus in dem Atomkern Erbium, dem 68. Element im Periodensystem, anschaute, erkannte er eine auffallende Ähnlichkeit. Die allgemeine Übereinstimmung zwischen einem gewissen Ausschnitt der Nullstellenorte auf der kritischen Geraden und den experimentell bestimmten Energieniveaus zeugte von großer Signifikanz.[86]
Durch umfassenden Einsatz von Computern wurde die Vermutung von Montgomery über die Nullstellenabstände von Andrew Odlyzko überprüft. Die Zahlen sprachen dabei für Montgomerys Annahme. 1987 publizierte Odlyzko seine Ergebnisse.[87]
Trotz starker Evidenzen wurden die Ergebnisse teilweise skeptisch gesehen. Es kam die Frage auf, ob damit irgendwelche Fortschritte in der reinen Mathematik erzielt worden waren. So äußerte der Zahlentheoretiker Peter Sarnak aus Princeton:
„Es ist ja recht faszinierend, die gleichen Bilder in beiden Gebieten zu sehen, doch wer kann einen wirklichen Beitrag zur Zahlentheorie nennen, der dadurch erst möglich geworden ist?“
Jonathan Keating, ein Schüler des Physikers Michael Berry, lieferte schon bald eine zahlentheoretische Anwendung. Berry hatte sich zuvor schon mit Zusammenhängen zwischen Primzahlen und Quantenphysik beschäftigt (insbesondere Verbindungen zum Quantenchaos). Doch es waren schließlich Keating und seine Doktorandin Nina Snaith, die mit Hilfe statistischer Methoden (die häufig in der Quantenphysik zum Einsatz kommen) eine exakte Formel für das durchschnittliche Verhalten von Potenzen der Absolutwerte der Zeta-Funktion entlang der kritischen Geraden aufstellten. Diese Durchschnittswerte sind für die Zahlentheorie von Bedeutung und haben viele Anwendungen, zum Beispiel auf das Dirichletsche Teilerproblem. Wenige Minuten vor Keatings Vorstellung der Ergebnisse hatte er zusammen mit Snaith die Formel an einer Tafel „getestet“, indem sie schauten, ob ein bereits mühsam erarbeitetes Ergebnis korrekt vorausgesagt würde. Das Besondere an der Herangehensweise von Keating und Snaith, die unter anderem von Atle Selberg gelobt wurde[89], war, dass sie Primzahlen dabei als Zufallsvariablen, also gewissermaßen Resultate eines Münzwurfes interpretierten. Sarnak lenkte ein, dass ohne diesen fremdartigen Ansatz eine solche Vermutung über die Zeta-Funktion nicht hätte erarbeitet werden können.[90]
Montgomerys Paarkorrelations-Vermutung und das asymptotische Verhalten der Zeta-Momente sind bis heute Gegenstand intensiver Forschung.
Die Riemannsche Vermutung bis heute[Bearbeiten | Quelltext bearbeiten]
Spätestens nachdem Hilbert die Riemannsche Vermutung auf die Liste seiner Probleme genommen hatte, erweckte sie das Interesse zahlreicher Mathematiker. Doch bis heute erweist sich das Problem als außerordentlich schwierig.
Nachdem 1942 Atle Selberg gezeigt hatte, dass ein positiver Anteil der Nullstellen auf der kritischen Geraden liegen muss, entwickelte sich daraus ein wahrer Wettlauf um die Größe dieses Anteils. Norman Levinson zeigte, dass gut ein Drittel die Vermutung erfüllen, und Brian Conrey zeigte 1989, dass es sogar gut 40 Prozent sind. Ob diese Methoden aber letztlich zu einer Lösung führen, gilt als umstritten. Nicht mal ein solcher Beweis, dass „100 Prozent“ (in einem asymptotischen Sinn) der Nullstellen der Vermutung gehorchen, wäre zwingend zielführend, da die Anzahl der Nullstellen unendlich groß ist. Ähnliche Bedenken existieren gegenüber den unternommenen Anstrengungen, nullstellenfreie Regionen zu optimieren.
Stephen Smale, Träger der Fields-Medaille, veröffentlichte 1998 seine eigene – im Sinne von Hilbert verfasste – Liste von 18 Problemen. Problem Nummer 1 ist die Riemannsche Vermutung. Bisher wurden nur wenige Probleme auf Smales Liste gelöst (siehe Smale-Probleme).
Weitere Berühmtheit erlangte die Riemannsche Vermutung, als sie im Jahr 2000 vom Clay Mathematics Institute (CMI) auf die Liste der Millennium-Probleme gesetzt wurde.[91] Für einen schlüssigen Beweis ist damit ein Preisgeld von 1 Million US-Dollar ausgelobt.
Praktische Anwendungsgebiete[Bearbeiten | Quelltext bearbeiten]
Es werden im Folgenden Anwendungen mit praktischem Bezug gegeben. Beziehungen zur mathematischen und physikalischen Grundlagenforschung finden sich weiter unten in den Bereichen:
- Analytische Zahlentheorie
- Algebraische Zahlentheorie und Geometrie
- Automorphe Formen
- Wahrscheinlichkeitstheorie und Statistik
Schnelle Primzahltests[Bearbeiten | Quelltext bearbeiten]
Ein Primzahltest ist ein Algorithmus, der überprüft, ob eine gegebene Zahl eine Primzahl ist. Verfährt man hier völlig naiv, muss dafür nachgerechnet werden, ob eine der Zahlen mit ein Teiler von ist. Teilt keine dieser Zahlen




















































































































































![{\displaystyle [N,M]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc6d045c399db081514f94dece322a4710309f69)











































































